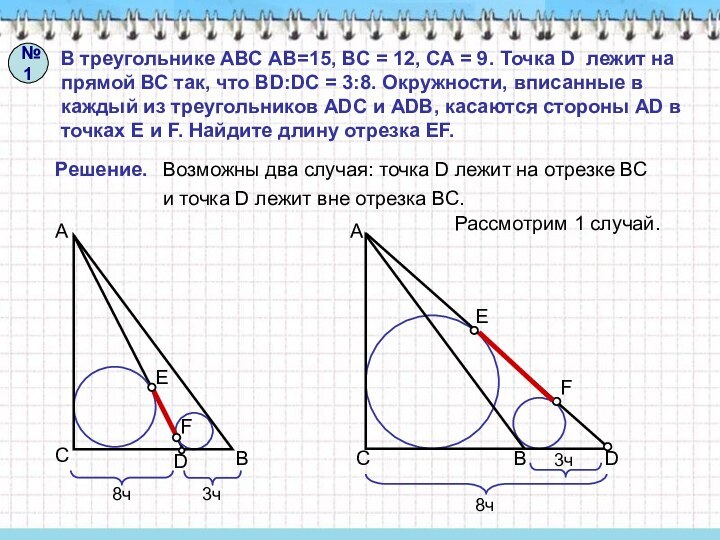
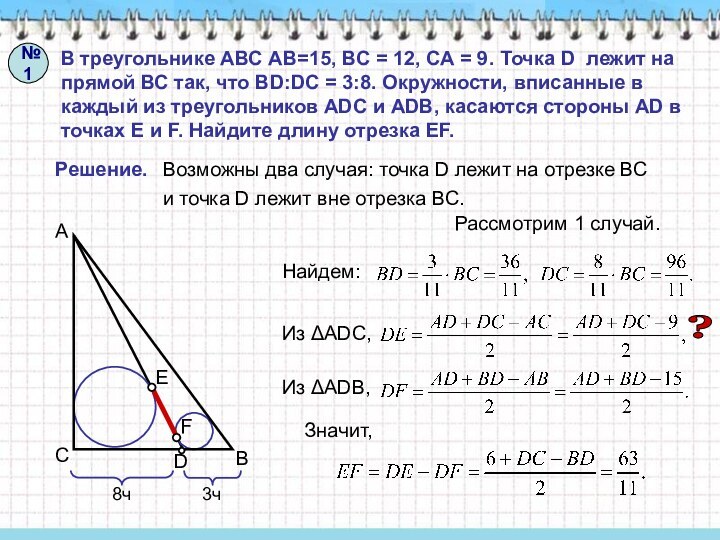
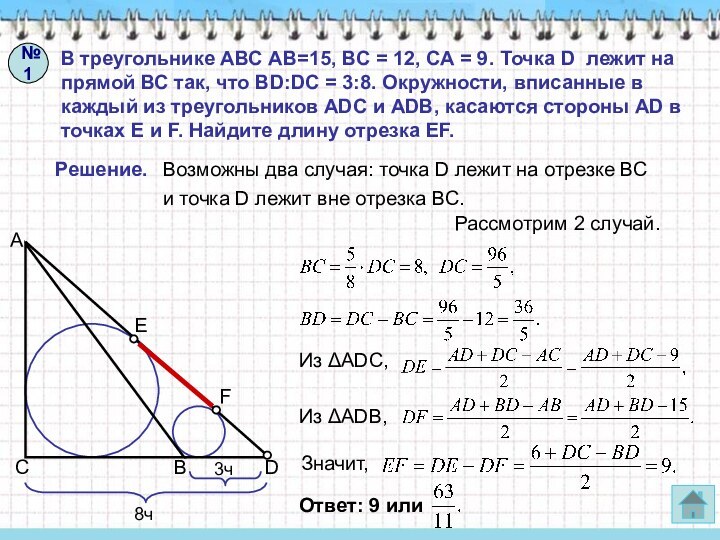
= 9. Точка D лежит на прямой ВС так,
что BD:DC = 3:8. Окружности, вписанные в каждый из треугольников ADC и ADB, касаются стороны AD в точках E и F. Найдите длину отрезка EF.Решение.
Возможны два случая: точка D лежит на отрезке ВС
и точка D лежит вне отрезка ВС.
Рассмотрим 1 случай.
№1