Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

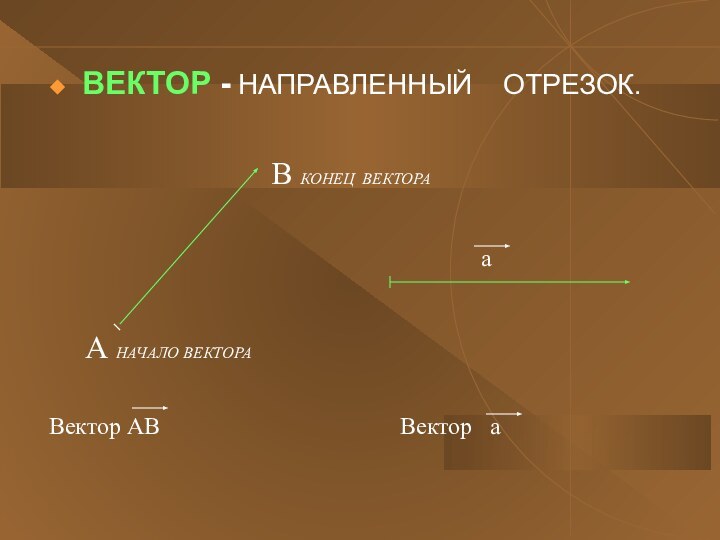
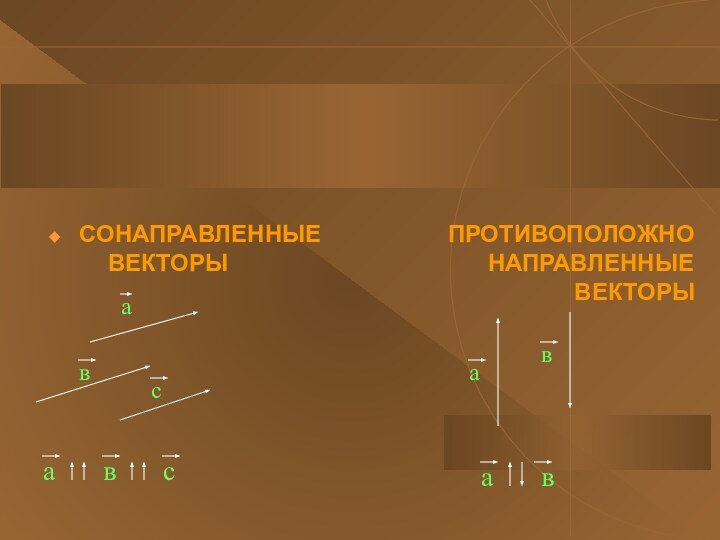
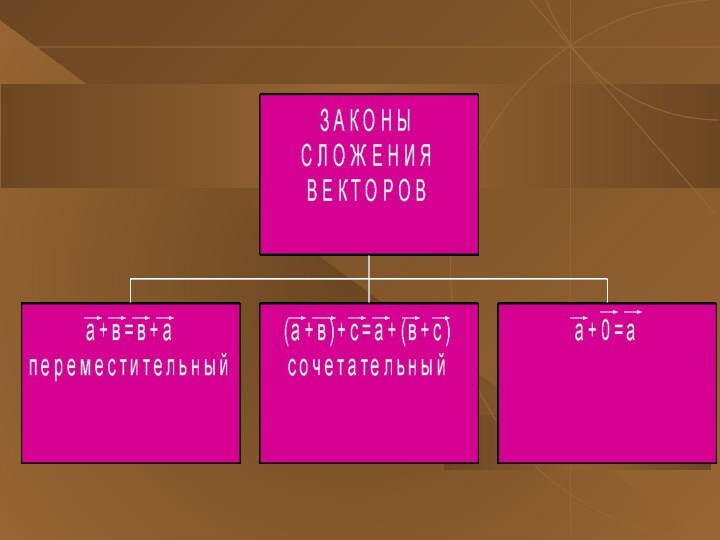
Презентация на тему Геометрия 9 класс Векторы

Содержание

2. Понятие вектораМногие физические величины, характеризуются не только
3. ИсторияВ 19 веке параллельно с теорией систем
4. ВЕКТОР - НАПРАВЛЕННЫЙ ОТРЕЗОК.В КОНЕЦ
5. Р а в е н с т
6. Д л и н а
7. СОНАПРАВЛЕННЫЕ
8. К О Л Л И Н Е
9. С Л О Ж Е
11. В Ы Ч И Т А Н
12. З А К Р Е П Л
13. 3).На рис. 3 изображён треугольник МNL Найти:
14. 4).На рис.4 изображён параллелограмм MNKE. Найти:MN + MEME + EKKN + KEMNKEРис.4
15. Разложение вектора на плоскости по двум неколлинеарным
16. Координаты вектораРазложение вектора по координатным векторам. Координатные
17. Простейшие задачи в координатах:1.Координаты середины отрезка2. Вычисление длины вектора по его координатам.3. Расстояние между двумя точками.
18. П Р О В Е Р Ь
19. П Р О В Е Р Ь
20. 1. а) да 2. а)
21. Скачать презентацию
22. Похожие презентации

Понятие вектораМногие физические величины, характеризуются не только своим числовым значением, но и направлением в пространстве. Такие физические величины называются ВЕКТОРАМИ.Проверь себя! Какие из данных величин являются векторными: вес, сила, отрезок, ускорение, скорость, масса ?

ИсторияВ 19 веке параллельно с теорией систем линейных уравнений развивалась теория векторов.

ВЕКТОР - НАПРАВЛЕННЫЙ ОТРЕЗОК.В КОНЕЦ ВЕКТОРАА НАЧАЛО ВЕКТОРАВектор АВ

3).На рис. 3 изображён треугольник МNL Найти: а) MN + NL б)

4).На рис.4 изображён параллелограмм MNKE. Найти:MN + MEME + EKKN + KEMNKEРис.4

Разложение вектора на плоскости по двум неколлинеарным векторамЕсли векторы a и b

Координаты вектораРазложение вектора по координатным векторам. Координатные векторы направлены вдоль осей координат.

Простейшие задачи в координатах:1.Координаты середины отрезка2. Вычисление длины вектора по его координатам.3. Расстояние между двумя точками.

Слайды презентации

Слайд 2 Понятие вектора
Многие физические величины, характеризуются не только своим

Понятие вектораМногие физические величины, характеризуются не только своим числовым значением, но

числовым значением, но и направлением в пространстве.

Такие физические

величины называются ВЕКТОРАМИ.

Проверь себя! Какие из данных величин являются векторными: вес, сила, отрезок, ускорение, скорость, масса ?

Слайд 3 История
В 19 веке параллельно с теорией систем линейных

ИсторияВ 19 веке параллельно с теорией систем линейных уравнений развивалась теория

уравнений развивалась теория векторов. Направленные отрезки использовал Жан Робер

АРГАН (Argand, 1768-1822, швейцарский математик), ввел термин «модуль комплексного числа» (1814-1815) в работе «Опыт некоторого представления мнимых величин…», опубликованной в 1806 году. Эти отрезки Арган обозначал символами а ,в .
Одним из основателей теории векторов считается Август Фердинанд Мебиус (1790-1868, немецкий математик), он обозначал отрезок с началом в точке А и концом в точке В символом АВ.
Термин «вектор» ввел Вильям Роуэн Гамильтон (1805-1865, директор астрономической обсерватории Дублинского университета и президент Ирландской Академии наук) приблизительно в 1845 году. Он же определил скалярное и векторное произведения векторов в 1853 году. Символ [а,в] для обозначения векторного произведения ввел немецкий математик и физик Герман Грасман (1809-1877).
В 1903 году О.Хенричи предложил обозначать скалярное произведение символом (а,в).

Слайд 4
ВЕКТОР - НАПРАВЛЕННЫЙ ОТРЕЗОК.
В КОНЕЦ ВЕКТОРА
А

НАЧАЛО ВЕКТОРА
Вектор АВ

Вектор а

Слайд 5 Р а в е н с т в

о в е к т о р о

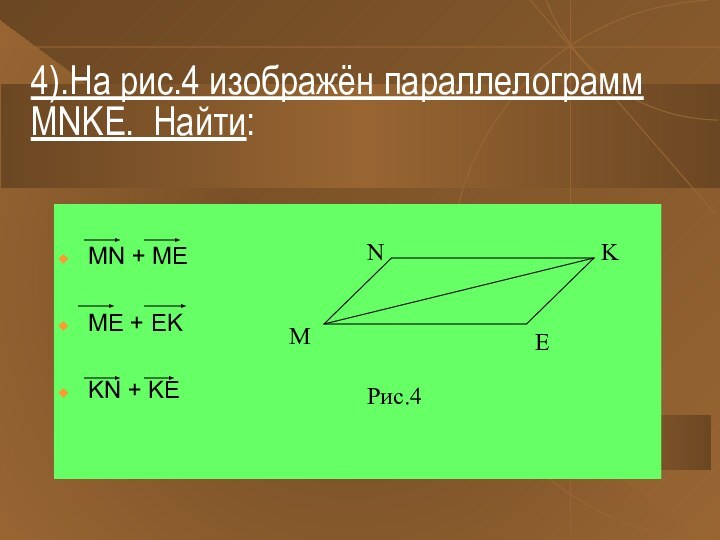
ВЕКТОРЫ называются равными, если они сонаправлены и их длины равны. .

а = в, если а в и а = в .

Слайд 6 Д л и н а в

е к т о р а
Длиной или модулем

ненулевого вектора АВ
называется длина отрезка АВ
.Обозначается длина вектора АВ (вектора а ) так :

АВ ( а ).

Длина нулевого вектора равна нулю: 0 = 0

Слайд 7 СОНАПРАВЛЕННЫЕ

ПРОТИВОПОЛОЖНО

ВЕКТОРЫ НАПРАВЛЕННЫЕ ВЕКТОРЫ

Слайд 8 К О Л Л И Н Е А

Р Н Ы Е В Е К

Т О Р Ы

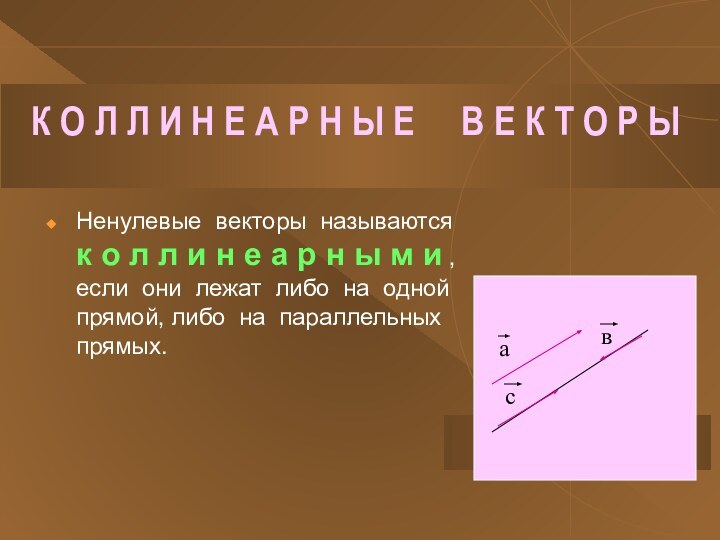
Ненулевые векторы называются к о л л и н е а р н ы м и , если они лежат либо на одной прямой, либо на параллельных прямых.

Слайд 9 С Л О Ж Е Н

И Е В Е К Т О Р

О В

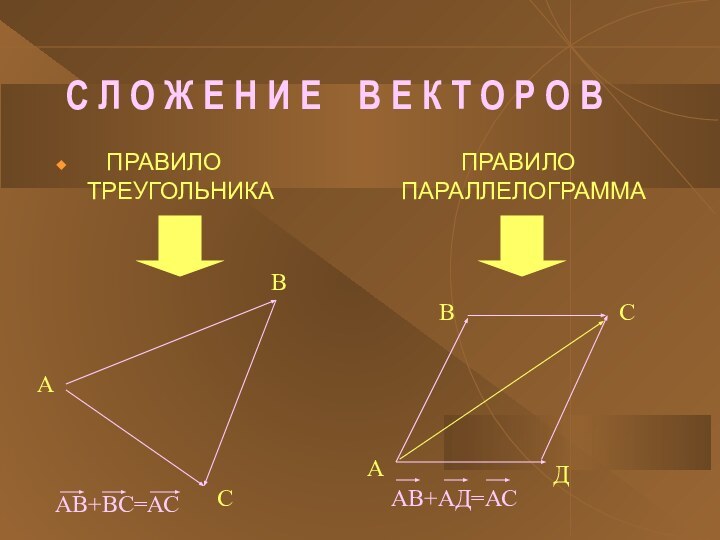
ПРАВИЛО ПРАВИЛО ТРЕУГОЛЬНИКА ПАРАЛЛЕЛОГРАММА

АВ+ВС=АС

АВ+АД=АС

Слайд 10

Слайд 11 В Ы Ч И Т А Н И

Е В Е К Т О Р О

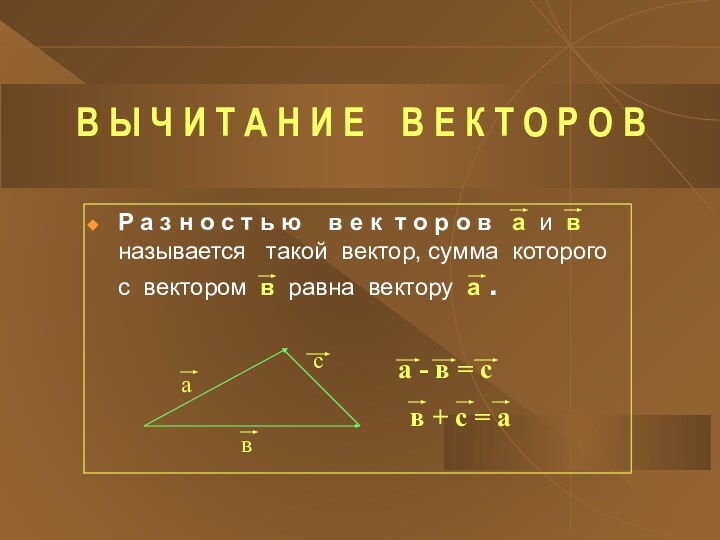
Р а з н о с т ь ю в е к т о р о в а и в называется такой вектор, сумма которого с вектором в равна вектору а .

а - в = с

в + с = а

Слайд 12 З А К Р Е П Л Е

Н И Е И З У Ч Е

Н Н О Г О

З А Д А Н И Я (устно)
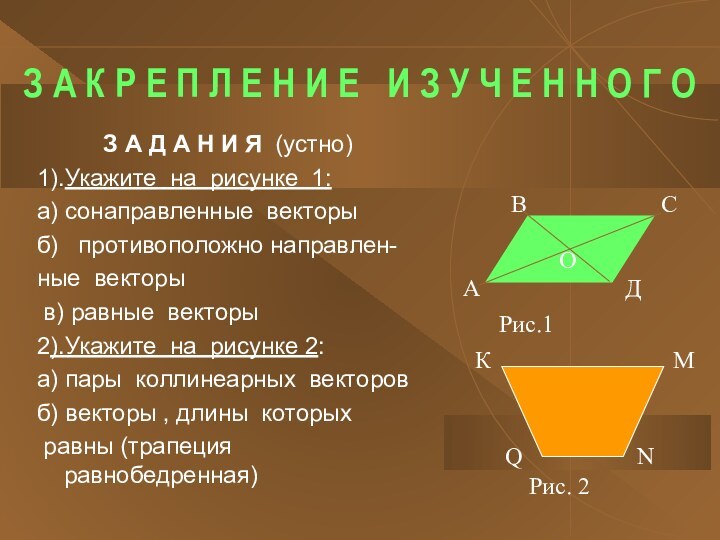
1).Укажите на рисунке 1:
а) сонаправленные векторы
б) противоположно направлен-
ные векторы
в) равные векторы
2).Укажите на рисунке 2:
а) пары коллинеарных векторов
б) векторы , длины которых
равны (трапеция равнобедренная)

Рис.1

Рис. 2

Слайд 13 3).На рис. 3 изображён треугольник МNL Найти:

а) MN

3).На рис. 3 изображён треугольник МNL Найти: а) MN + NL

+ NL

б) MN - ML

в )

ML - MN

Рис.3

Слайд 14 4).На рис.4 изображён параллелограмм MNKE. Найти:

MN + ME

ME +

EK

KN + KE
M
N
K
E
Рис.4

Слайд 15 Разложение вектора на плоскости по двум неколлинеарным векторам
Если

Разложение вектора на плоскости по двум неколлинеарным векторамЕсли векторы a и

векторы a и b коллинеарны и а ≠0, то

существует такое число k, что в=k а.
Любой вектор можно разложить по двум данным неколлинеарным вектора, причем коэффициенты разложения определяются единственным образом.
с=xа+ув, где х и у коэффициенты разложения.

Слайд 16 Координаты вектора
Разложение вектора по координатным векторам. Координатные векторы

Координаты вектораРазложение вектора по координатным векторам. Координатные векторы направлены вдоль осей

направлены вдоль осей координат. Длины этих
векторов

равны 1
Обозначения: i(1;0), j(0;1)
Любой вектор а можно разложить единственным образом по координатным векторам: а=хi+уj
а{x;y} –координаты вектора а

Слайд 17 Простейшие задачи в координатах:
1.Координаты середины отрезка
2. Вычисление длины

вектора по его координатам.
3. Расстояние между двумя точками.

Слайд 18 П Р О В Е Р Ь

С Е Б Я !

1). Верно ли утверждение:
а)

Если а=в , то а в
б) Если а=в , то а и в коллинеарны
в) Если а=в , то а в
г) Если а в , то а = в
2). Дан прямоугольник PQRT. Найти:
а) PQ + QR
б) PT - PQ
в) RT + RQ

Слайд 19 П Р О В Е Р Ь

С Е Б Я !

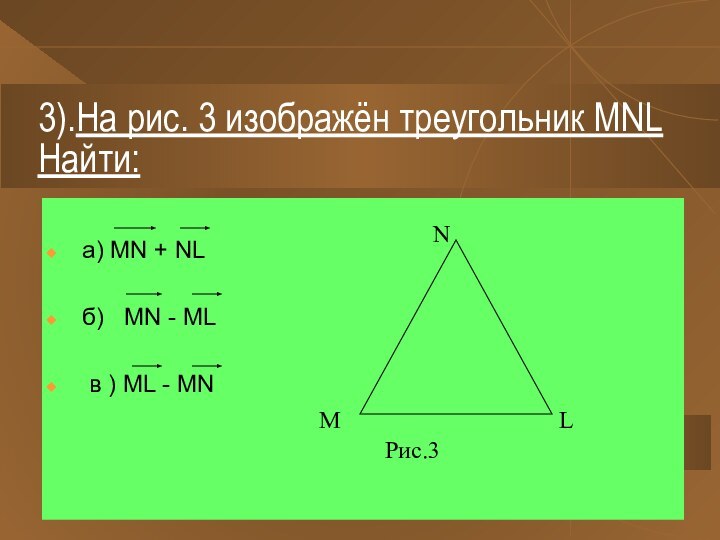
3) Найдите вектор х из условия:
EF- LM- EL+ x =MK
4) Выпишите координаты вектора с, если его разложение по координатным векторам имеет вид с = -6i +2j
5) Дано а{-2;4}, d{3;-1}. Найдите координаты вектора
к =2а –d
6) OA- радиус-вектор точки А, ОА{-5;4}.Какие координаты имеет точка А?
7) Найти координаты вектора RT? Если R(-1;5) , T(6;2).
8) Найдите длину вектора s{3;4}