Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Случайные величины и их числовые характеристики

Содержание

Случайной называется величина, которая в результате опыта может принять то или иное возможное значение, неизвестное заранее, но обязательно одно.
Кафедра математики и моделированияСтарший преподаватель Е.Г. ГусевКурс «Высшая математика»Лекция 15. Тема: Случайные Случайной называется величина, которая в результате опыта может принять то или иное Дискретной случайной величиной называют такую случайную величину, множество возможных значений которой Непрерывной случайной величиной называют такую случайную величину, которая может принять любое значение Случайные величины: ; Законом распределения дискретной случайной величины называется всякое соотношение, устанавливающее связь между возможными Закон распределения случайной величины можно задать, как и функцию: табличным, графическим и аналитическим способами. Две случайные величины называются независимыми, если закон распределения вероятностей одной из них Если - функция распределения, то Если Если - дискретная случайная величина, то …………………………………………........... Дифференциальной функцией распределения или плотностью распределения вероятностей наз. первая производная интегральной функции распределения График дифференциальной функции распределения наз. кривой распределения: 1.Для 2.Для имеет место равенство3. 4.Свойства плотности распределения вероятности. Числовые характеристики случайных величин. Математическое ожидание. Математическим ожиданиемдискретной случайной величины наз.сумма произведений всех возможныхзначений Пусть случайная величина приняла значения Причем Математическим ожиданием непрерывной случайной величины , возможные значения Свойства математического ожидания 1. 2. 3.Если Пример 1. Пример 2. Дисперсия Математическое ожидание квадрата отклонения СВ от её математического Если СВ - дискретная СВ, то Если СВ Среднее квадратическое отклонение Свойства дисперсии1. 2.3.4. 5. Вопросы:1)Определения дискретной случайной величины и непрерывной случайной величины?2)Числовые характеристики ДСВ?3)Числовые характеристики НСВ?
Слайды презентации

Слайд 2
Случайной называется величина, которая в результате опыта может

Случайной называется величина, которая в результате опыта может принять то или

принять то или иное возможное значение, неизвестное заранее, но

обязательно одно.

Слайд 3
Дискретной случайной величиной называют такую случайную величину,

Дискретной случайной величиной называют такую случайную величину, множество возможных значений

множество возможных значений которой либо конечно, либо бесконечно, но

обязательно счетно.

Слайд 4

Непрерывной случайной величиной называют такую случайную величину, которая

Непрерывной случайной величиной называют такую случайную величину, которая может принять любое

может принять любое значение из некоторого конечного или бесконечного

интервала.

Слайд 5

Случайные величины:

Случайные величины: ; значения: .

;


значения:

.

Слайд 6

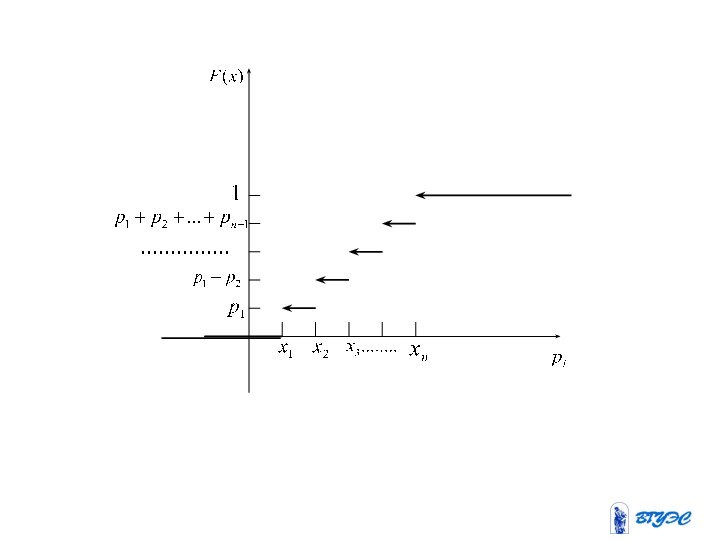
Законом распределения дискретной случайной величины называется всякое соотношение,

Законом распределения дискретной случайной величины называется всякое соотношение, устанавливающее связь между

устанавливающее связь между возможными значениями случайной величины и соответствующими

вероятностями.

Слайд 7
Закон распределения случайной величины можно задать, как и

Закон распределения случайной величины можно задать, как и функцию: табличным, графическим и аналитическим способами.

функцию: табличным, графическим и аналитическим способами.

Слайд 8

Две случайные величины называются независимыми, если закон распределения

Две случайные величины называются независимыми, если закон распределения вероятностей одной из

вероятностей одной из них не зависит от того какие

возможные значения приняла другая.

Слайд 9 Если - функция

Если - функция распределения, то Если - непрерывная

распределения,
то


Если - непрерывная случайная

величина, то .

Слайд 10
Если - дискретная случайная величина,

Если - дискретная случайная величина, то



то





Слайд 11



…………………………………………...........

…………………………………………...........

Слайд 12

Слайд 13

Слайд 14

Дифференциальной функцией распределения или плотностью распределения

Дифференциальной функцией распределения или плотностью распределения вероятностей наз. первая производная интегральной функции распределения

вероятностей наз. первая производная интегральной функции распределения

Слайд 15 График дифференциальной функции распределения

График дифференциальной функции распределения наз. кривой распределения:

наз. кривой распределения:

Слайд 16


1.Для
2.Для имеет место

1.Для 2.Для имеет место равенство3. 4.Свойства плотности распределения вероятности.

равенство


3.

4.
Свойства плотности
распределения вероятности.

Слайд 17 Числовые характеристики случайных величин.

Числовые характеристики случайных величин.

Слайд 18







Математическое ожидание.

Математическое ожидание.

Слайд 19 Математическим ожиданием
дискретной случайной величины

Математическим ожиданиемдискретной случайной величины наз.сумма произведений всех возможныхзначений случайной

наз.
сумма произведений всех возможных
значений случайной величины на
соответствующие вероятности появления

этих значений:

Слайд 20 Пусть случайная величина

Пусть случайная величина приняла значения Причем появилось

приняла значения
Причем появилось

раз,
появилось раз,
……………………….,
появилось раз.



где

Слайд 21 Математическим ожиданием непрерывной случайной величины

Математическим ожиданием непрерывной случайной величины , возможные значения которой

, возможные значения которой принадлежат

, называется



Если возможные значения принадлежат

, то

Слайд 22 Свойства математического ожидания
1.
2.
3.Если

Свойства математического ожидания 1. 2. 3.Если независимые случайные

независимые случайные величины, то

4.Если независимые случайные величины, то

5.

Слайд 23 Пример 1.

Пример 1.

Слайд 24 Пример 2.

Пример 2.

Слайд 25

Слайд 26 Дисперсия
Математическое ожидание квадрата отклонения СВ

Дисперсия Математическое ожидание квадрата отклонения СВ от её математического ожидания

от её математического ожидания называют

дисперсией СВ :


Слайд 27 Если СВ - дискретная

Если СВ - дискретная СВ, то Если СВ

СВ, то




Если СВ -

дискретная СВ, то

Слайд 28

Среднее квадратическое отклонение

Среднее квадратическое отклонение


Слайд 29 Свойства дисперсии
1.
2.
3.
4.
5.

Свойства дисперсии1. 2.3.4. 5.
  • Имя файла: sluchaynye-velichiny-i-ih-chislovye-harakteristiki.pptx
  • Количество просмотров: 111
  • Количество скачиваний: 1
- Предыдущая Русская Православная Церковь
Следующая - Магічні квадрати

Похожие презентации

Виды треугольников Виды треугольников 104
Основные типы задач на проценты Основные типы задач на проценты 118
Презентация математика!.. презентация к уроку по математике (3 класс) Презентация математика!.. презентация к уроку по математике (3 класс) 119
Презентация по математике на тему Этот удивительный симметричный мир(6класс) Презентация по математике на тему Этот удивительный симметричный мир(6класс) 49
prezentatsiya1 - kopiya - prezentatsiya1 - kopiya - 107
Делимость чисел 8 класс Делимость чисел 8 класс 125
Двойные интегралы Двойные интегралы 237
Прямоугольник. Измерение площадей фигур Прямоугольник. Измерение площадей фигур 113
Переместительное свойство сложения методическая разработка по математике (1 класс) по теме Переместительное свойство сложения методическая разработка по математике (1 класс) по теме 108
Презентация по математике Письменные приемы сложения и вычитания 4 класс презентация к уроку по математике (4 класс) Презентация по математике Письменные приемы сложения и вычитания 4 класс презентация к уроку по математике (4 класс) 115
Презентация внеклассного мероприятия по математике Математическая сказка 5 класс Презентация внеклассного мероприятия по математике Математическая сказка 5 класс 116
Подготовка к ЕГЭ-2019 по математике Подготовка к ЕГЭ-2019 по математике 156
Стандартный вид числа Стандартный вид числа 98
Применение нескольких способов разложения многочлена на множители Применение нескольких способов разложения многочлена на множители 109
Презентация к уроку Скорость.Время. Расстояние презентация к уроку по математике (3 класс) по теме Презентация к уроку Скорость.Время. Расстояние презентация к уроку по математике (3 класс) по теме 110
ეკონომიკისა და ბიზნესის სტატისტიკა. ცენტრალური ტენდენციის მახასიათებლები. თემა 2 ეკონომიკისა და ბიზნესის სტატისტიკა. ცენტრალური ტენდენციის მახასიათებლები. თემა 2 158
презентация к уроку математики 3 класс презентация к уроку математики (3 класс) презентация к уроку математики 3 класс презентация к уроку математики (3 класс) 113
Умножение натуральных чисел Умножение натуральных чисел 109
Урок математики 2 класс Урок математики 2 класс 142
Конспект открытого занятия по математике в старшей группе Путешествие в страну Математики презентация к уроку по математике (старшая группа) Конспект открытого занятия по математике в старшей группе Путешествие в страну Математики презентация к уроку по математике (старшая группа) 281
Презентация по математике Столбчатые диаграммы(6 класс) Презентация по математике Столбчатые диаграммы(6 класс) 197
Единицы времени Единицы времени 147
Сказки зимнего леса. план-конспект занятия по математике (старшая группа) по теме Сказки зимнего леса. план-конспект занятия по математике (старшая группа) по теме 147
Тренажёр Сложение и вычитание круглых чисел в пределах 100 Тренажёр Сложение и вычитание круглых чисел в пределах 100 140
Математика. 1 класс. Урок 51. Число 10 - Презентация презентация к уроку (математика, 1 класс) по теме Математика. 1 класс. Урок 51. Число 10 - Презентация презентация к уроку (математика, 1 класс) по теме 144
Волшебный квадрат 9 класс Волшебный квадрат 9 класс 126
Лента Мёбиуса Лента Мёбиуса 91
Устный счет Устный счет 85
Измерение длины 1 класс презентация к уроку по математике (1 класс) Измерение длины 1 класс презентация к уроку по математике (1 класс) 121
Урок-презентация Урок-презентация 105