- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Геометрия Подобные треугольники
Содержание
- 2. Урок 32. Пропорциональные отрезки.Рассмотрим пропорцию:Отрезки называются пропорциональными,
- 3. Свойство биссектрисы треугольника.Биссектриса треугольника делит противоположную сторону
- 4. Урок 33. Подобные треугольники.Два треугольника называются подобными,
- 5. № 541.АВСDEF10634106404,45,27,615,622,813,2Решение задач: № 542.Домашнее задание: п.56-57, № 540.
- 6. Урок 34. Теорема об отношении площадей подобных
- 7. Урок 35. Первый признак подобия треугольников.АВСА1В1С1ТЕОРЕМА.Если 2
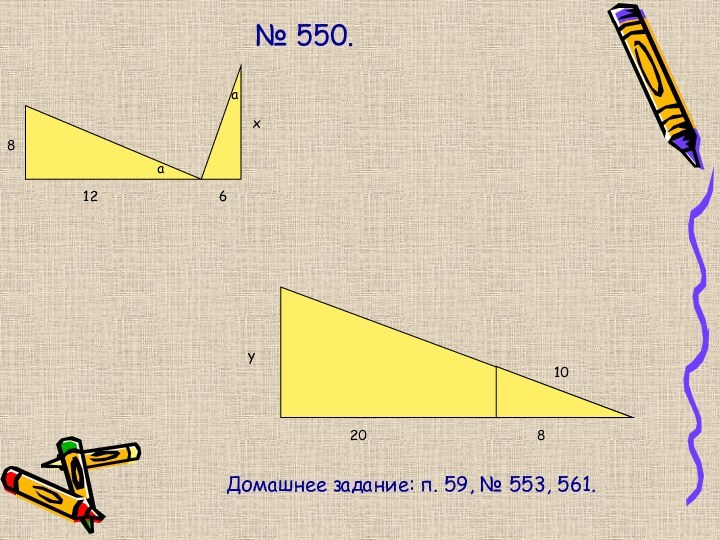
- 8. № 550.812аа6xy20810Домашнее задание: п. 59, № 553, 561.
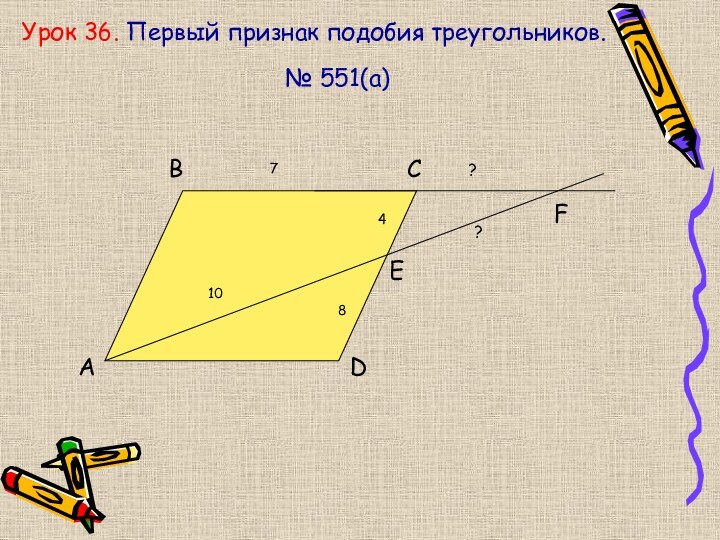
- 9. Урок 36. Первый признак подобия треугольников.№ 551(а)ABCDEF1048??7
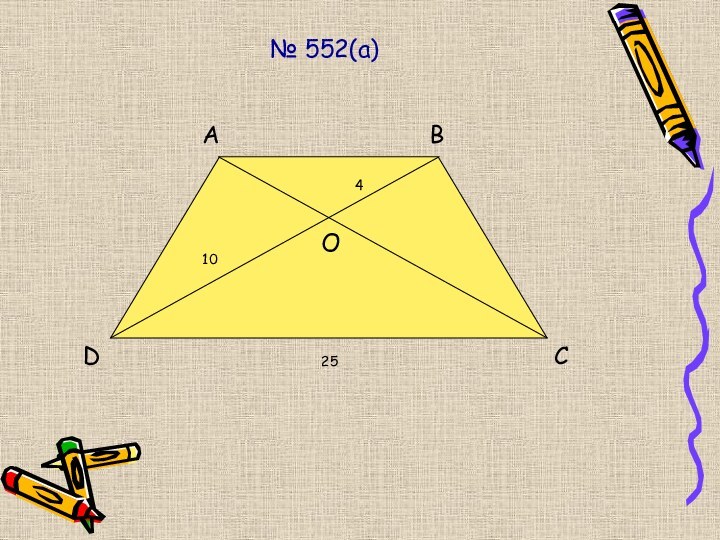
- 10. № 552(а)ABCDO25104
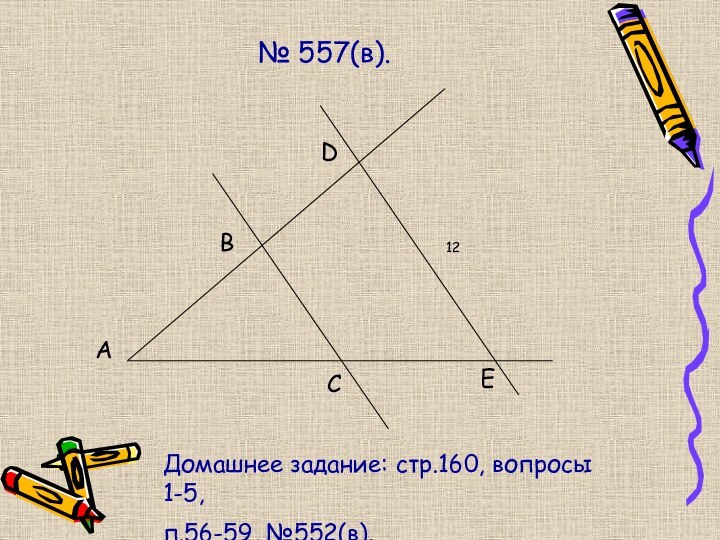
- 11. № 557(в).ABDCE12Домашнее задание: стр.160, вопросы 1-5,п.56-59, №552(в).
- 12. Урок 37. Второй признак подобия треугольников.ТЕОРЕМА. Если
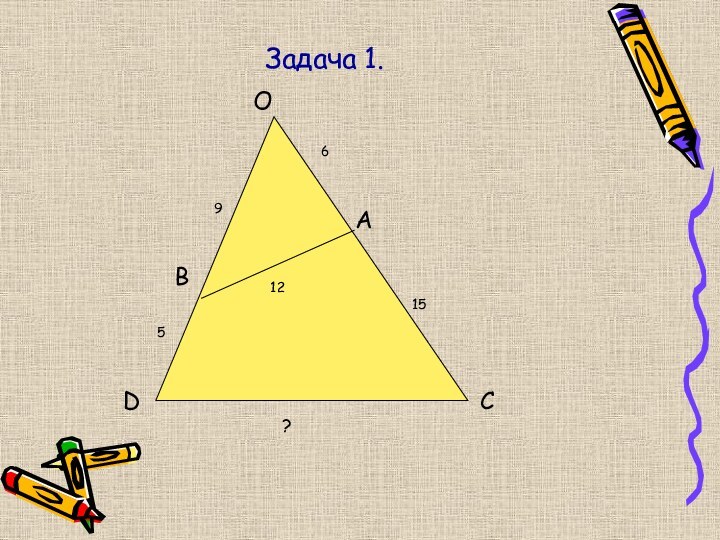
- 13. Задача 1.DBOAC5961512?
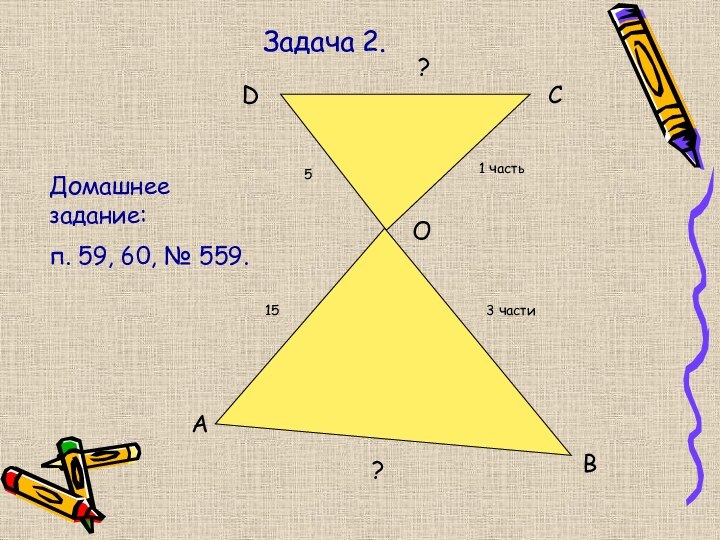
- 14. Задача 2.DCOBA155 1 часть3 части??Домашнее задание: п. 59, 60, № 559.
- 15. Задача.АВСКРМСтороны треугольника АВС в 2,5 раза больше
- 16. Урок 38. Третий признак подобия треугольников.ТЕОРЕМА. Если
- 17. Задачи.Подобны ли ∆АВС и ∆КРМ, если АВ
- 18. Математический диктант.Третий признак подобия треугольников.Второй признак подобия
- 19. Ответы.По 3 пропорциональ-ным сторонам.По 2 пропорциональ-ным сторонам
- 20. Подобие прямоугольных треугольников.Два прямоугольных треугольника подобны, если:У
- 21. Задача.ABCDO18121510Доказать, что ABCD – трапеция.
- 22. № 554.ABMCD83,63,95Домашнее задание: п. 59-61,Стр. 160, вопросы
- 23. Урок 39. Средняя линия треугольника.ТЕОРЕМА.Средняя линия треугольника
- 24. Решение задач.№ 564.№ 570.875АВСDMO18Домашнее задание: п. 62, № 566.
- 25. Математический диктант.Две стороны треугольника соединили отрезком, непараллельным
- 26. Ответы.Нет Средняя линия24 смНет Средняя линия8 см6 дмНет
- 27. Задачи.Дано:РАВС= 12 смНайти: РМРОАВСМРО2. Дано:AD=2BC, MB=MK,NC=NK, BC=6 смНайти PQAPBCQDMN63. Дано: АС=10см, BD=8смНайти РMNPKABCDKMNP
- 28. Урок 40. Пропорциональные отрезки в прямоугольном треугольнике.Признак
- 29. Решение задач: № 572, 575, 577.Домашнее задание:стр.160,
- 30. Урок 42. Синус, косинус и тангенс
- 31. Основное тригонометрическое тождество.Решение задач: № 591(а,б), 592(а,в,д), 593(а,в).Домашнее задание: п.66, № 593(б,г), 592(б,г,е), 591(в,г).
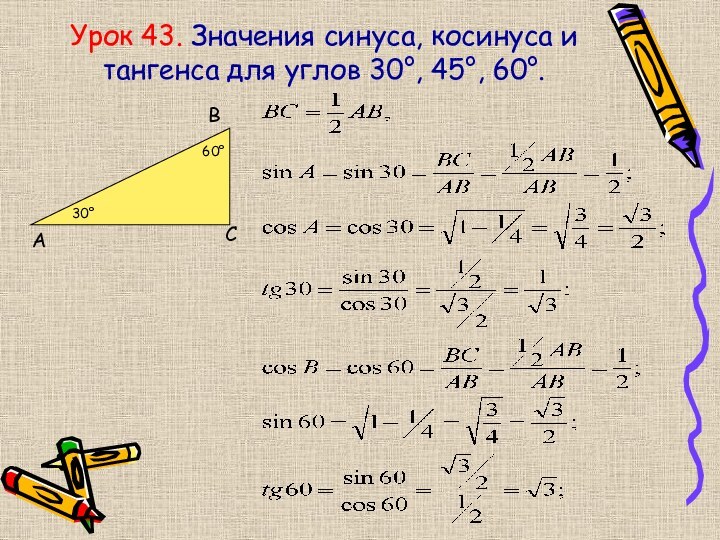
- 32. Урок 43. Значения синуса, косинуса и тангенса для углов 30°, 45°, 60°.АВС30°60°
- 33. Урок 43. Значения синуса, косинуса и тангенса
- 34. Решение задач.Найти площадь равнобедренного прямоугольного треугольника с
- 35. Контрольная работа № 4.Средняя линия равнобед-ренного треугольника,
- 36. Скачать презентацию
- 37. Похожие презентации














Слайд 2
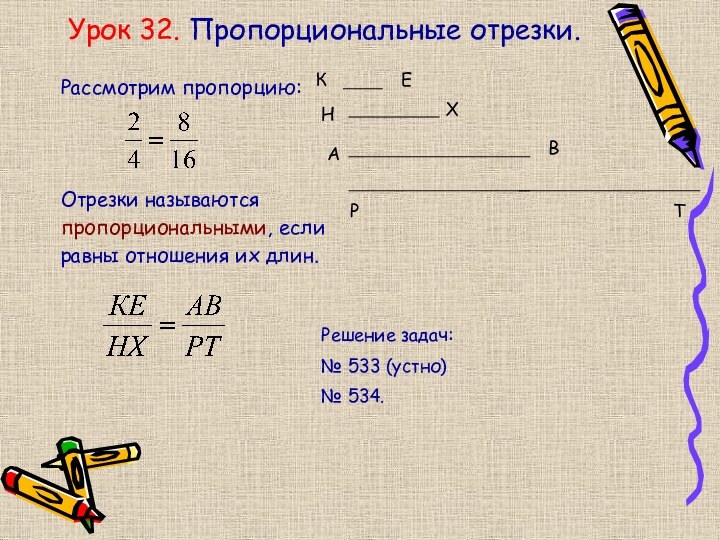
Урок 32. Пропорциональные отрезки.
Рассмотрим пропорцию:
Отрезки называются
пропорциональными, если
Слайд 3
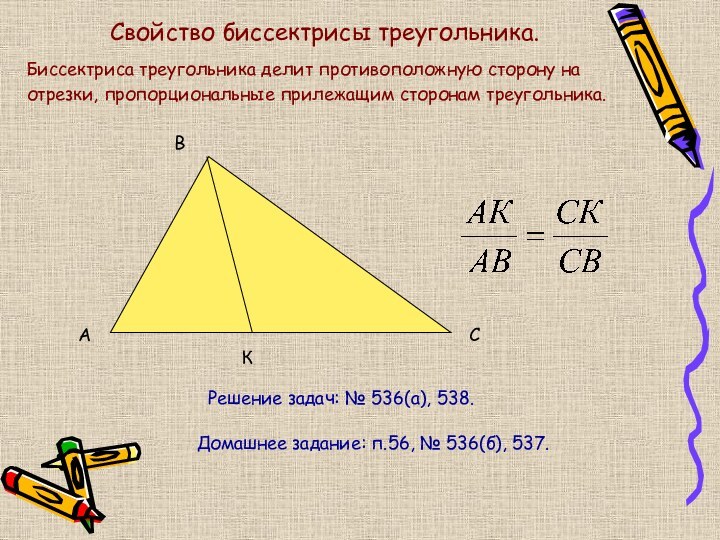
Свойство биссектрисы треугольника.
Биссектриса треугольника делит противоположную сторону на
отрезки, пропорциональные прилежащим сторонам треугольника.
А
В
С
К
Решение задач: № 536(а), 538.
Домашнее
задание: п.56, № 536(б), 537.
Слайд 4
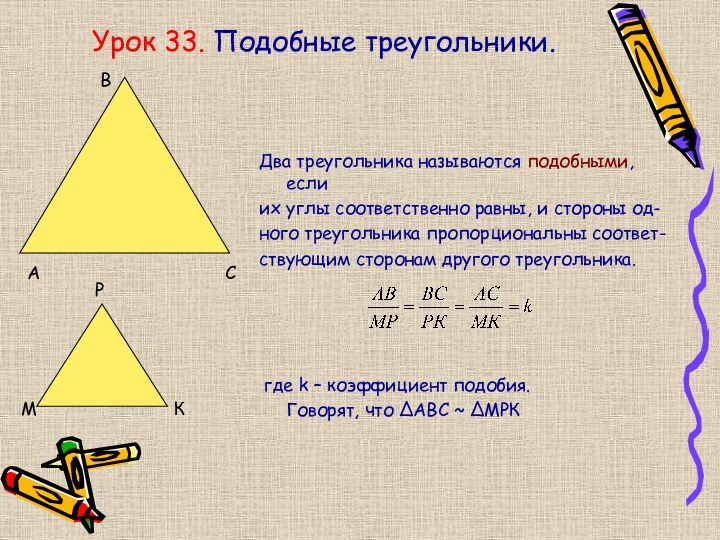
Урок 33. Подобные треугольники.
Два треугольника называются подобными, если
их углы соответственно равны, и стороны од-
ного треугольника пропорциональны
соответ-ствующим сторонам другого треугольника.
где k – коэффициент подобия.
Говорят, что ∆АВС ~ ∆МРК
А
В
С
М
Р
К
Слайд 5
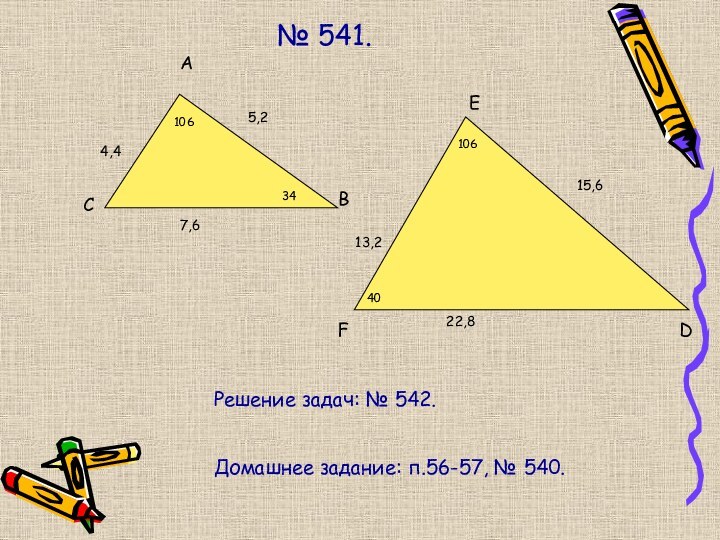
№ 541.
А
В
С
D
E
F
106
34
106
40
4,4
5,2
7,6
15,6
22,8
13,2
Решение задач: № 542.
Домашнее задание: п.56-57, №
540.
Слайд 6
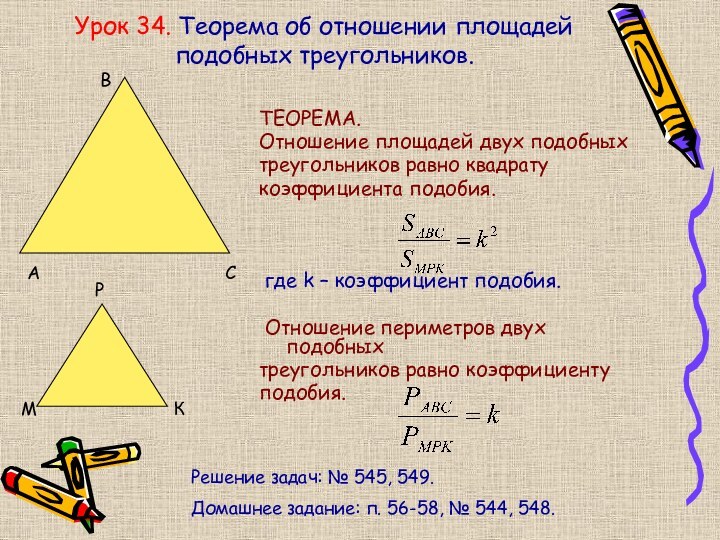
Урок 34. Теорема об отношении площадей подобных треугольников.
ТЕОРЕМА.
Отношение
площадей двух подобных
треугольников равно квадрату
коэффициента подобия.
где k – коэффициент подобия.
Отношение периметров двух подобных
треугольников равно коэффициенту
подобия.
А
В
С
М
Р
К
Решение задач: № 545, 549.
Домашнее задание: п. 56-58, № 544, 548.
Слайд 7
Урок 35. Первый признак подобия треугольников.
А
В
С
А1
В1
С1
ТЕОРЕМА.
Если 2 угла
одного треугольника равны соответственно двум углам другого треугольника, то
такие треугольники подобны.Доказательство: Так как углы А=А1 и С=С1, то угол В=В1.
Так как угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих эти углы.
Следовательно, ∆АВС ~ ∆А1В1С1
Слайд 12
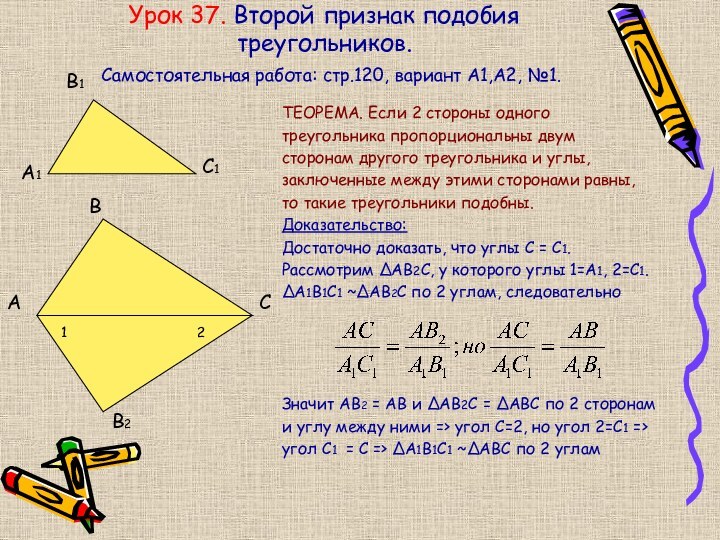
Урок 37. Второй признак подобия треугольников.
ТЕОРЕМА. Если 2
стороны одного
треугольника пропорциональны двум
сторонам другого треугольника и
углы, заключенные между этими сторонами равны,
то такие треугольники подобны.
Доказательство:
Достаточно доказать, что углы С = С1.
Рассмотрим ∆АВ2С, у которого углы 1=А1, 2=С1.
∆А1В1С1 ~∆АВ2С по 2 углам, следовательно
Значит АВ2 = АВ и ∆АВ2С = ∆АВС по 2 сторонам
и углу между ними => угол С=2, но угол 2=С1 =>
угол С1 = С => ∆А1В1С1 ~∆АВС по 2 углам
Самостоятельная работа: стр.120, вариант А1,А2, №1.
А1
В1
С1
А
В
С
В2
1
2
Слайд 15
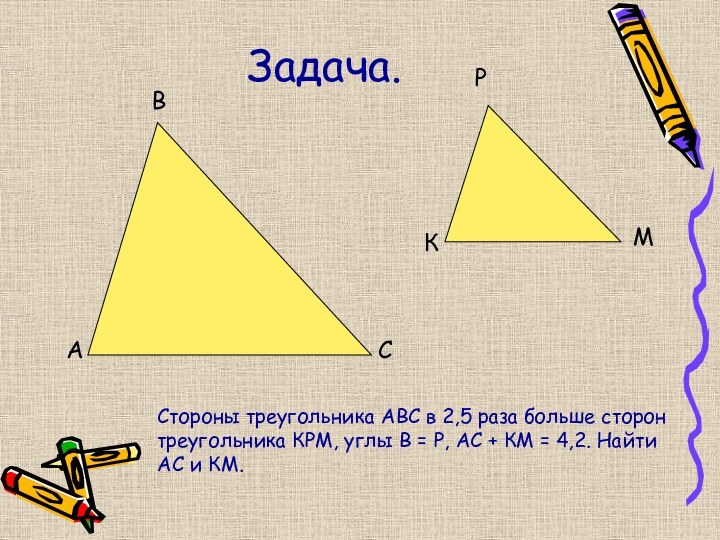
Задача.
А
В
С
К
Р
М
Стороны треугольника АВС в 2,5 раза больше сторон
треугольника КРМ, углы В = Р, АС + КМ
= 4,2. Найти АС и КМ.
Слайд 16
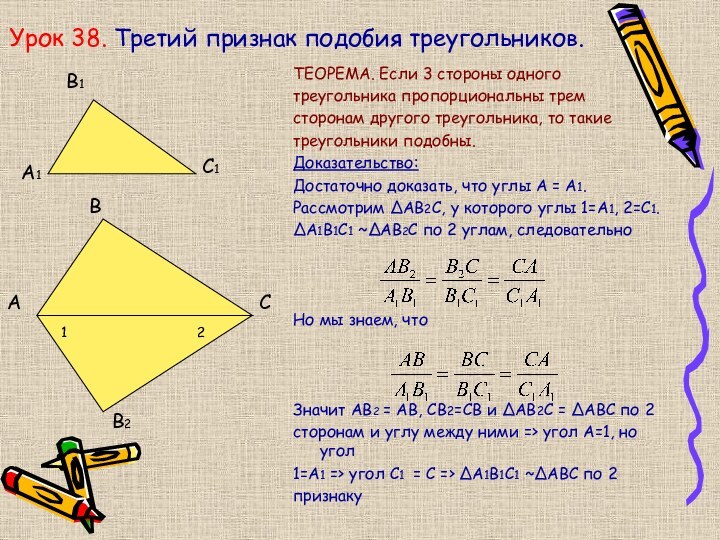
Урок 38. Третий признак подобия треугольников.
ТЕОРЕМА. Если 3
стороны одного
треугольника пропорциональны трем
сторонам другого треугольника, то
такие треугольники подобны.
Доказательство:
Достаточно доказать, что углы А = А1.
Рассмотрим ∆АВ2С, у которого углы 1=А1, 2=С1.
∆А1В1С1 ~∆АВ2С по 2 углам, следовательно
Но мы знаем, что
Значит АВ2 = АВ, СВ2=СВ и ∆АВ2С = ∆АВС по 2
сторонам и углу между ними => угол А=1, но угол
1=А1 => угол С1 = С => ∆А1В1С1 ~∆АВС по 2
признаку
А1
В1
С1
А
В
С
В2
1
2
Слайд 17
Задачи.
Подобны ли ∆АВС и ∆КРМ, если АВ =
1м, АС = 2м, ВС = 1,5 м, КР
= 8 дм, КМ = 16 дм, РМ = 12 дм.Стороны треугольника равны 0,8 м, 1,6 м, 2 м. Найти стороны подобного ему треугольника, периметр которого равен 5,5 м.
Домашнее задание: п. 59-61, № 560.
Слайд 18
Математический диктант.
Третий признак подобия треугольников.
Второй признак подобия треугольников.
У
двух треугольников по одному равному углу. Какого условия недостает,
чтобы треугольники были подобны по 1 признаку?Стороны одного треугольника равны 3 см, 6 см и 7 см, а 2 стороны подобного ему треугольника равны 15 см и 35 см. Найти третью сторону.
Соответствующие катеты двух подобных треугольников 6 дм и 18 дм. Найти гипотенузу меньшего треугольника, если гипотенуза большего 27 дм.
Первый признак подобия треугольников.
Третий признак подобия треугольников.
У двух треугольников по одному равному углу. Какого условия недостает, чтобы треугольники были подобны по 2 признаку?
Соответствующие катеты двух подобных треугольников 5 дм и 10 дм. Найти гипотенузу большего треугольника, если гипотенуза меньшего 7 дм.
Стороны одного треугольника равны 15 см, 35 см и 30 см, а 2 стороны подобного ему треугольника равны 6 см и 7 см. Найти третью сторону.
Слайд 19
Ответы.
По 3 пропорциональ-ным сторонам.
По 2 пропорциональ-ным сторонам и
углу между ними.
Пара равных углов.
30 см.
9 дм.
По 2 равным
углам.По 3 пропорциональным сторонам.
Пропорциональность сторон угла.
14 дм.
3 м.
Слайд 20
Подобие прямоугольных треугольников.
Два прямоугольных треугольника подобны, если:
У них
есть по равному острому углу.
Катеты одного треугольника пропорциональны катетам
другого треугольника.Гипотенуза и катет одного треугольника пропорциональны гипотенузе и катету другого треугольника.
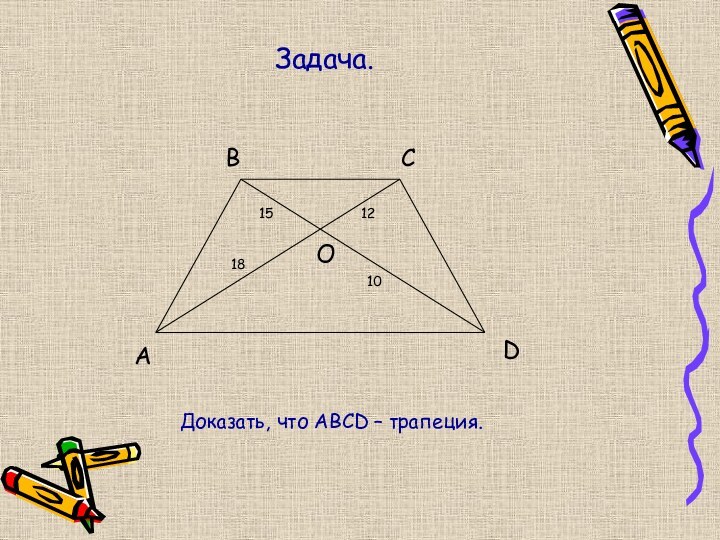
Слайд 22
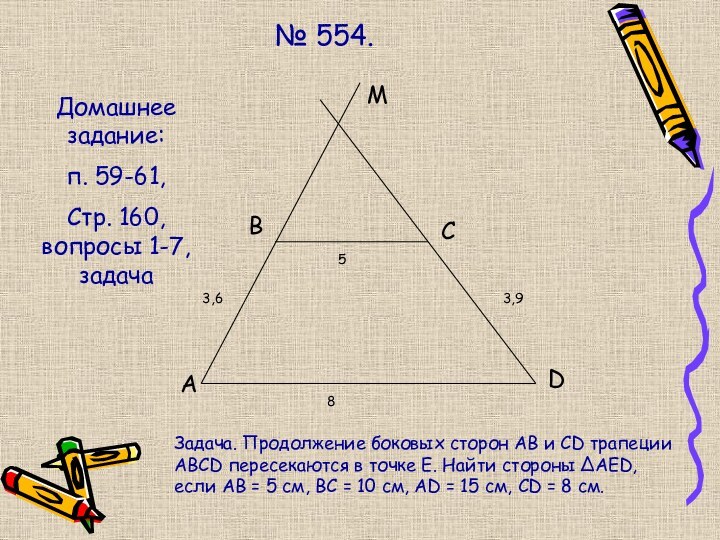
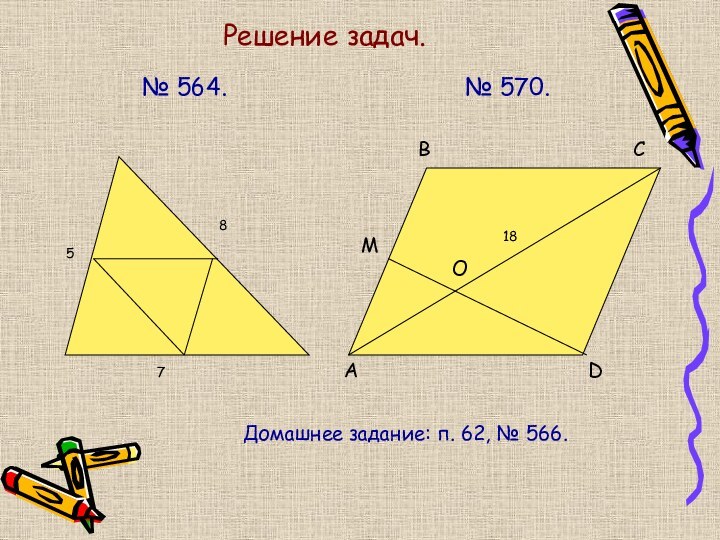
№ 554.
A
B
M
C
D
8
3,6
3,9
5
Домашнее задание:
п. 59-61,
Стр. 160, вопросы 1-7,
задача
Задача. Продолжение боковых сторон АВ и CD трапеции ABCD
пересекаются в точке Е. Найти стороны ∆АЕD, если АВ = 5 см, ВС = 10 см, АD = 15 см, СD = 8 см.
Слайд 23
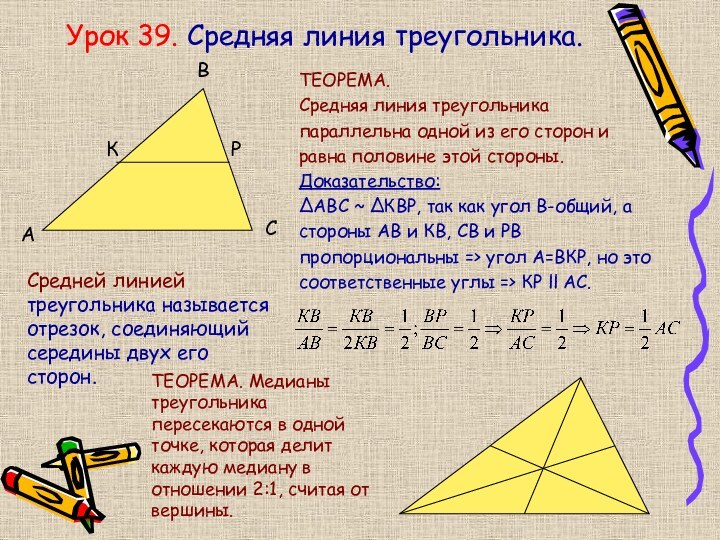
Урок 39. Средняя линия треугольника.
ТЕОРЕМА.
Средняя линия треугольника
параллельна
одной из его сторон и
равна половине этой стороны.
Доказательство:
∆АВС
~ ∆КВР, так как угол В-общий, а стороны АВ и КВ, СВ и РВ
пропорциональны => угол А=ВКР, но это
соответственные углы => КР ll АС.
А
В
С
К
Р
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
ТЕОРЕМА. Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.
Слайд 25
Математический диктант.
Две стороны треугольника соединили отрезком, непараллельным третьей
стороне. Является ли этот отрезок средней линией треугольника?
Сторона АВ
∆АВС равна 6 см. Чему равна средняя линия треугольника, параллельная этой стороне?Точки М, Р и О – середины сторон ∆АВС. Найти стороны ∆АВС, если стороны ∆МРО равны 3 см, 4 см и 5 см.
Концы отрезка АВ лежат на двух сторонах треугольника, а длина этого отрезка равна половине третьей стороны. Обязательно ли этот отрезок является средней линией треугольника?
Точки А и В являются серединами двух сторон треугольника. Как называется отрезок АВ?
Средней линией ∆АВС, параллельная стороне ВС, равна 4 см. Найти сторону ВС.
Точки А, В, С – середины сторон ∆МРО. Найти периметр ∆АВС, если отрезки МР, РО и МО равны 3 дм, 4 дм и 5 дм.
Концы отрезка КР лежат на двух сторонах треугольника, он параллелен третьей стороне треугольника и равен ее половине. Является ли КР средней линией?
Слайд 27
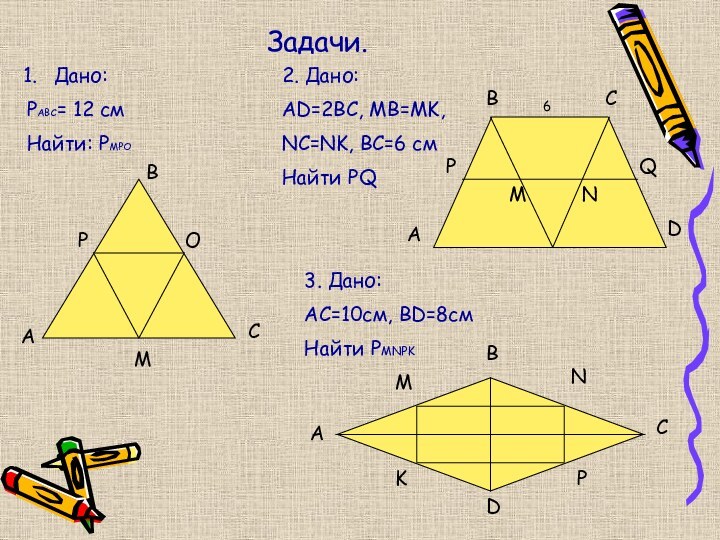
Задачи.
Дано:
РАВС= 12 см
Найти: РМРО
А
В
С
М
Р
О
2. Дано:
AD=2BC, MB=MK,
NC=NK, BC=6 см
Найти
PQ
A
P
B
C
Q
D
M
N
6
3. Дано:
АС=10см, BD=8см
Найти РMNPK
A
B
C
D
K
M
N
P
Слайд 28
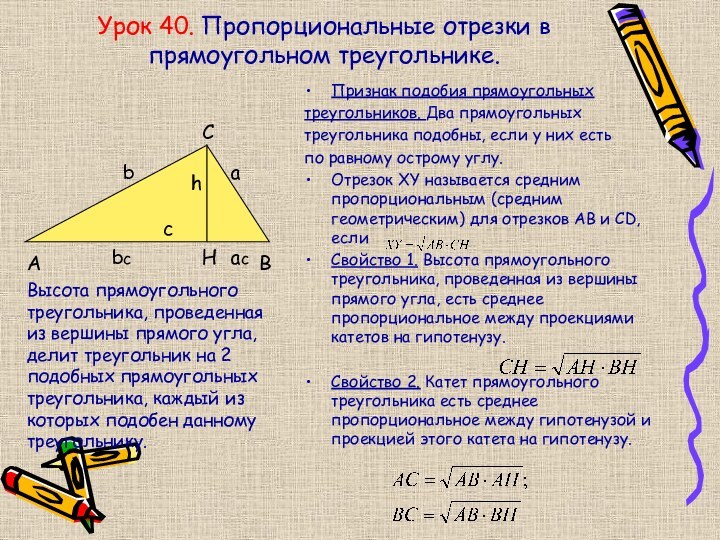
Урок 40. Пропорциональные отрезки в прямоугольном треугольнике.
Признак подобия
прямоугольных
треугольников. Два прямоугольных
треугольника подобны, если у них
есть по равному острому углу.
Отрезок XY называется средним пропорциональным (средним геометрическим) для отрезков АВ и CD, если
Свойство 1. Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу.
Свойство 2. Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу.
А
С
В
Н
Высота прямоугольного треугольника, проведенная из вершины прямого угла, делит треугольник на 2 подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
с
bc
ac
a
b
h
Слайд 29
Решение задач: № 572, 575, 577.
Домашнее задание:
стр.160, вопросы
8-11, принести циркуль,
№ 576, 578-в общую тетрадь.
Проверочная работа.
стр. 124,
вариант А1, А2,задачи 1, 2.
Слайд 30 Урок 42. Синус, косинус и тангенс острого угла
прямоугольного треугольника.
А
В
С
Синусом острого угла прямоугольного треугольника называется отношение
противолежащего катета к гипотенузе.Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Тангенс угла равен отношению синуса к косинусу этого угла.
α
β
Слайд 31
Основное тригонометрическое тождество.
Решение задач: № 591(а,б), 592(а,в,д), 593(а,в).
Домашнее
задание: п.66, № 593(б,г), 592(б,г,е), 591(в,г).
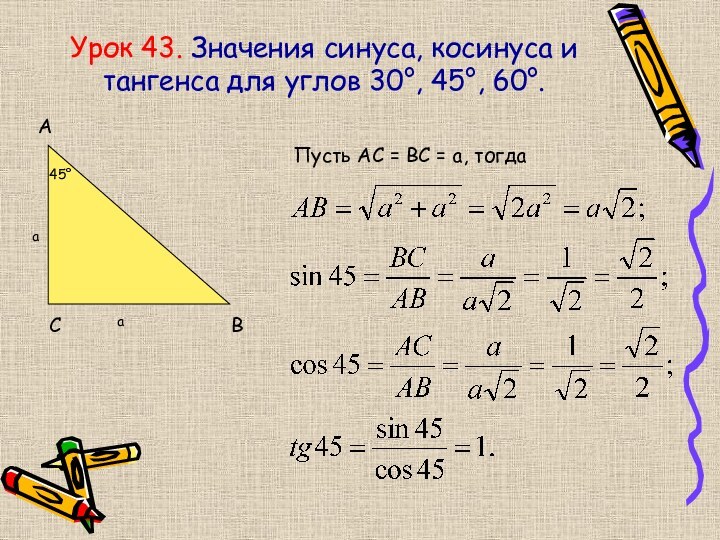
Слайд 33 Урок 43. Значения синуса, косинуса и тангенса для
углов 30°, 45°, 60°.
А
В
С
45°
Пусть АС = ВС = а,
тогдаа
а
Слайд 34
Решение задач.
Найти площадь равнобедренного прямоугольного треугольника с основанием
10 см и углом при основании 45°.
Найти катеты прямоугольного
треугольника, гипотенуза которого 2 см, один из острых углов 30°.В треугольнике АВС угол А=45°, угол С=60°, ВС=2 см. Найти АС.
№ 600.
Домашнее задание: п. 66, 67, № 602.
Слайд 35
Контрольная работа № 4.
Средняя линия равнобед-ренного треугольника, параллельная
боковой стороне, равна 13 см, а медиана, проведенная к
основанию - 24 см. Найти среднюю линию, парал-лельную основанию треугольника.Найти sin α и tg α, если cosα=8/17.
Найти синус, косинус тангенс большего острого угла прямоугольного треугольника с катетами 7 см и 24 см.
Средняя линия равнобед-ренного треугольника, параллельная основанию, равна 16 см, а биссект-риса, проведенная к основанию - 30 см. Найти среднюю линию, парал-лельную боковой стороне треугольника.
Найти cos α и tg α, если sinα=5/12.
Найти синус, косинус тангенс меньшего острого угла прямоугольного треугольника с катетом 40 см и гипотенузой 41 см.





























