- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Гипербола
Содержание
- 3. Введем обозначения:a – действительная полуось гиперболыb –
- 4. Прямые, проходящие через начало координат и имеющие
- 5. ТЕОРЕМАДля того, чтобы точка М(х,у) принадлежала гиперболе, необходимо и достаточно, чтобы ее координаты удовлетворяли уравнениюгде2
- 6. Покажем, что координаты точки, принадлежащей гиперболе, удовлетворяют
- 7. Тогда:
- 8. Возводим в квадрат обе части выражения:
- 9. Возводим в еще раз квадрат:Делим все выражение на
- 10. каноническое уравнение гиперболы
- 11. Отношение фокусного расстояния к длине действительной оси гиперболы называетсяЭКСЦЕНТРИСИТЕТОМ
- 12. Скачать презентацию
- 13. Похожие презентации
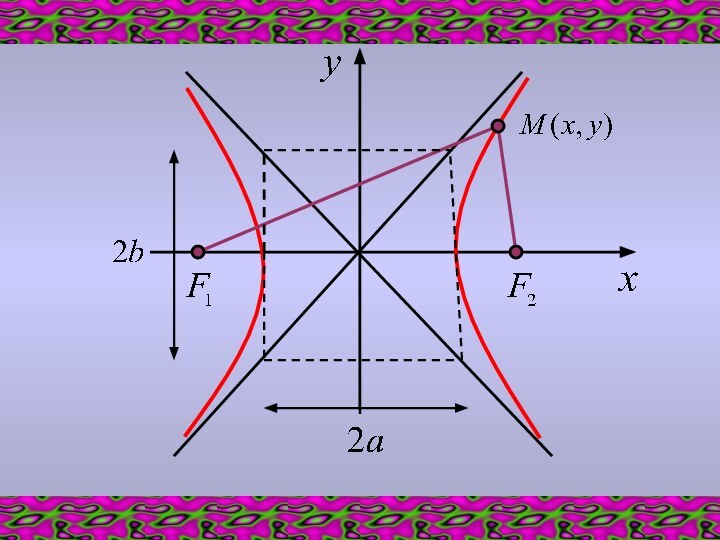
Введем обозначения:a – действительная полуось гиперболыb – мнимая полуось гиперболыДля любой точки М(х,у), принадлежащей гиперболе, по определению выполняется равенство:






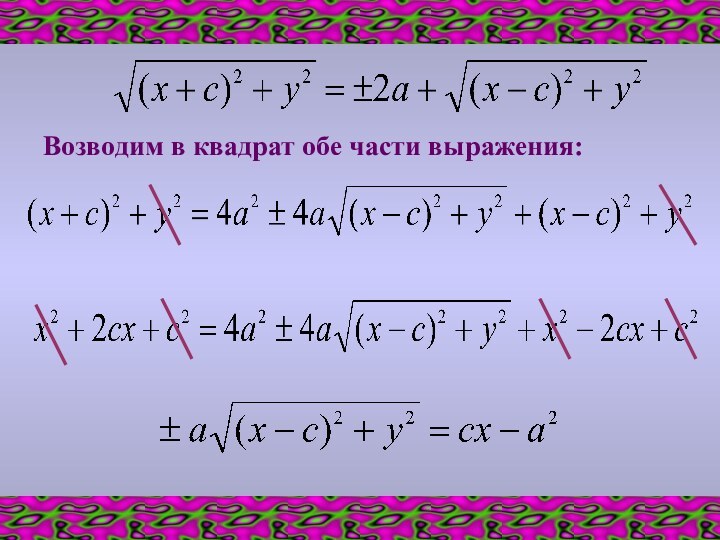
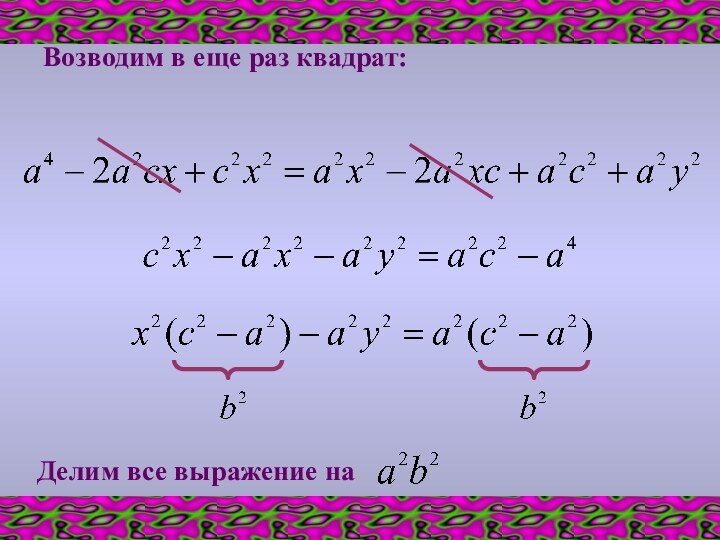



Слайд 3
Введем обозначения:
a – действительная полуось гиперболы
b – мнимая
полуось гиперболы
выполняется равенство:Слайд 4 Прямые, проходящие через начало координат и имеющие угловые
коэффициенты
и
называются асимптотами гиперболы.
Асимптоты делят плоскость на 4 области, в
двух из которых расположена гипербола.Точки гиперболы по мере удавления от оси у приближаются к асимптотам, т.е. расстояние между точками гиперболы и асимптотой при увеличении х уменьшается и стремится к нулю.
Слайд 5
ТЕОРЕМА
Для того, чтобы точка М(х,у) принадлежала гиперболе, необходимо
и достаточно, чтобы ее координаты удовлетворяли уравнению
где
2
Слайд 6 Покажем, что координаты точки, принадлежащей гиперболе, удовлетворяют уравнению
(2).
Т.к. точка М(х,у) принадлежит гиперболе, то по определению гиперболы,
должно выполнятся условиеВыразим каждое расстояние по формуле расстояния между двумя точками: