- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
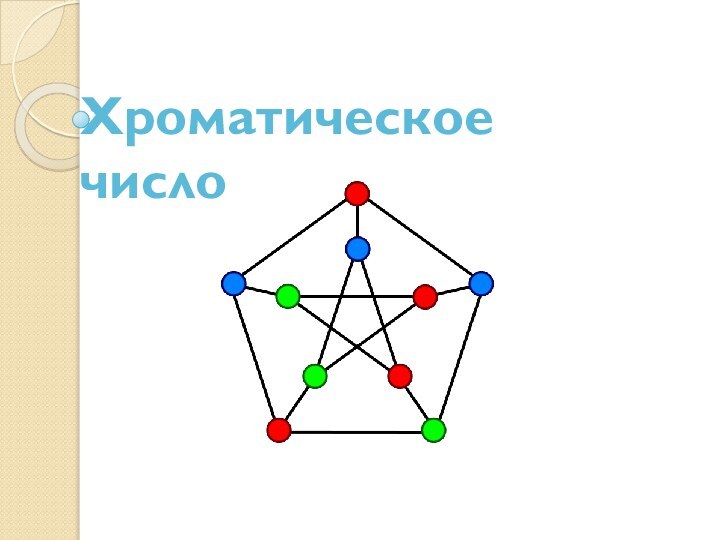
Презентация на тему Хроматическое число
Содержание
- 2. Определение. Пусть G=(V,E) – обыкновенный граф и
- 3. Наименьшее число красок, необходимое для правильной раскраски
- 4. Оба графа содержат трехэлементный полный подграф К3,
- 5. Очевидно, что если компоненты связности графа G
- 6. ТеоремаПусть любой блок графа G можно правильно
- 7. Приведем примеры задач, которые сводятся к нахождению хроматического числа и соответствующей оптимальной раскраски.
- 8. Задача составления расписаний. Предположим, что в учебном центре
- 9. Задача распределения ресурсов. Необходимо выполнить некоторое множество V={v1,v2,…,vn}
- 10. Задача экономии памяти. Предположим, что необходимо написать программу
- 12. Верхнюю часть можно назвать блок–схемой по информации.
- 13. Предположим, что значения переменной занимают одну ячейку
- 14. Скачать презентацию
- 15. Похожие презентации









Слайд 2
Определение.
Пусть G=(V,E) – обыкновенный граф и k
– натуральное число.
Раскраска называется правильной, если для любых смежных вершин x,y ϵ V справедливо неравенство f(x) ≠ f(y). Число k – число красок раскраски f.Слайд 3 Наименьшее число красок, необходимое для правильной раскраски графа
G называется хроматическим числом графа G.
Правильную раскраску таким числом
красок будем называть оптимальной.Хроматическое число обозначается через χ(G).
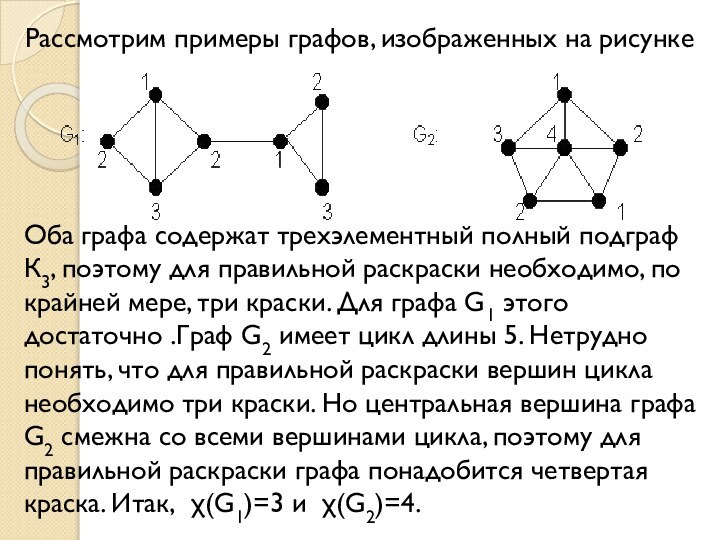
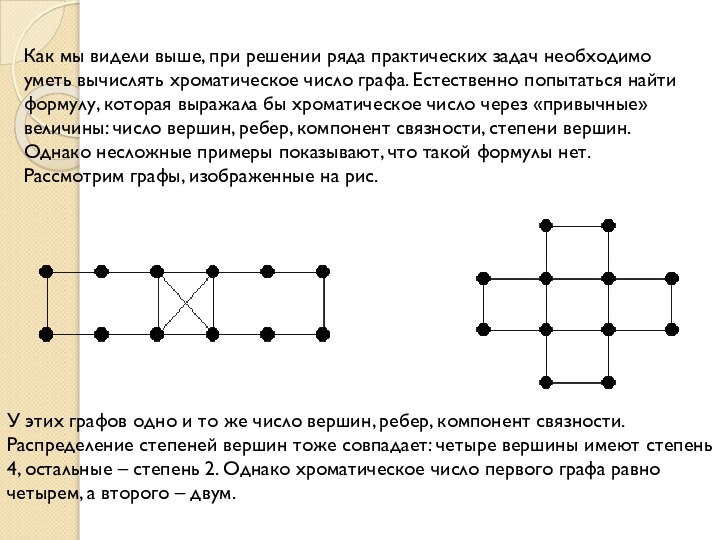
Слайд 4 Оба графа содержат трехэлементный полный подграф К3, поэтому
для правильной раскраски необходимо, по крайней мере, три краски.
Для графа G1 этого достаточно .Граф G2 имеет цикл длины 5. Нетрудно понять, что для правильной раскраски вершин цикла необходимо три краски. Но центральная вершина графа G2 смежна со всеми вершинами цикла, поэтому для правильной раскраски графа понадобится четвертая краска. Итак, χ(G1)=3 и χ(G2)=4.Рассмотрим примеры графов, изображенных на рисунке
Слайд 5 Очевидно, что если компоненты связности графа G правильно
раскрасить k красками, то и сам граф окажется правильно
раскрашенным этими красками. Отсюда следует, что если G1,G2,…,Gc – (все) компоненты связности графа G, тоχ(G)=max{χ(G1), χ(G2),…, χ(Gc)}.
Аналогичное утверждение справедливо и для компонент двусвязности.
Слайд 6
Теорема
Пусть любой блок графа G можно правильно раскрасить
k расками. Тогда и сам граф G можно правильно
раскрасить k красками.Доказательство проведем индукцией по числу блоков. Можно считать, что G – связный граф.
Если граф содержит один блок, то утверждение теоремы, очевидно, справедливо. Предположим, что теорема справедлива для любых графов, имеющих не более k блоков. Пусть граф G имеет k+1 блок. Зафиксируем один из концевых блоков графа G. Этот блок обозначим через В, а объединение остальных блоков – через В' . Графы В и В’ имеют точно одну общую вершину а (которая является точкой сочленения графа G). По предположению индукции графы В и В’ можно правильно раскрасить k красками. Если вершина а в обоих графах В и В’ окрашена одинаково, то в результате получаем правильную раскраску графа G. Если вершина а в графах В и В’ окрашена по-разному, то очевидным образом перекрашиваем граф В так, чтобы новая краска вершины а совпадала с краской этой вершины в графе В’.
Слайд 7 Приведем примеры задач, которые сводятся к нахождению хроматического
числа и соответствующей оптимальной раскраски.
Слайд 8 Задача составления расписаний. Предположим, что в учебном центре надо
провести несколько занятий за кратчайшее время. Длительность всех занятий
одинакова, скажем, один час. Некоторые занятия не могут проводиться одновременно, например, это занятия в одной и той же учебной группе (по разным предметам), или занятия проводит один и тот же преподаватель. Для решения задачи построим граф G, вершинам которого биективно соответствуют занятия. Две вершины соединены ребром, если соответствующие занятия нельзя проводить одновременно. Ясно, что правильная раскраска графа G определяет расписание, удовлетворяющее требованиям несовместимости по времени: занятия, соответствующие вершинам, окрашенным одинаково, можно проводить одновременно. Справедливо и обратное, любое такое расписание определяет правильную раскраску графа G. Следовательно, кратчайшее время необходимое для проведения всех занятий равно χ(G), а из оптимальной раскраски графа G получается необходимое расписание.
Слайд 9
Задача распределения ресурсов.
Необходимо выполнить некоторое множество V={v1,v2,…,vn} работ.
Имеется множество S={s1,s2,…,sr} ресурсов, необходимых для выполнения этих работ.
Каждая работа использует часть указанных ресурсов, одновременно могут выполняться работы, использующие разные ресурсы. Все работы выполняются за одно и то же время t. Необходимо распределить ресурсы так, чтобы общее время выполнения всех работ было минимальным.Рассмотрим граф G с множеством вершин V. Две различные вершины v и v’ графа G смежны тогда и только тогда, когда для выполнения работ v и v’ требуется хотя бы один общий ресурс. Наименьшее время выполнения всех работ равно χ(G)·t. Оптимальная раскраска графа G определяет распределение ресурсов.
Слайд 10
Задача экономии памяти.
Предположим, что необходимо написать программу для
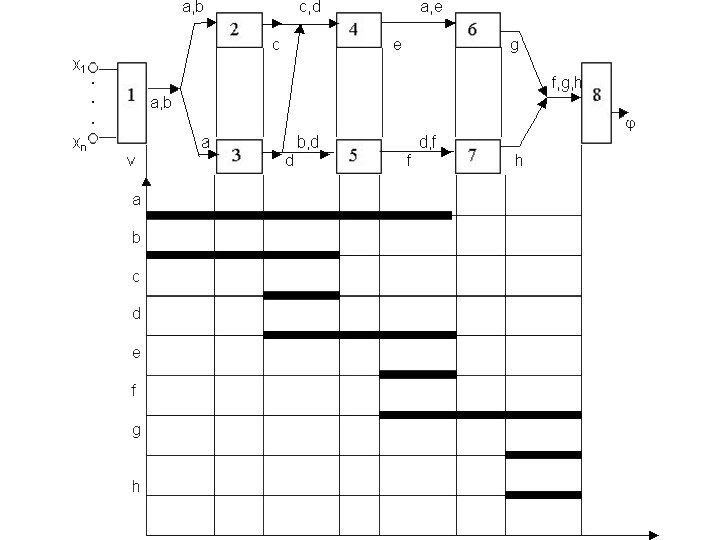
вычисления функции φ(х1,x2,…,xn). Вычисление этой функции разбито на ряд блоков,
у каждого из блоков имеются входные и выходные переменныеТак, например, у блока 2 входные переменные a и b, выходная – с, у блока 3 входная переменная a, выходная – d.
Слайд 12 Верхнюю часть можно назвать блок–схемой по информации. Нижняя
часть этого рисунка представляет собой «систему координат», где по
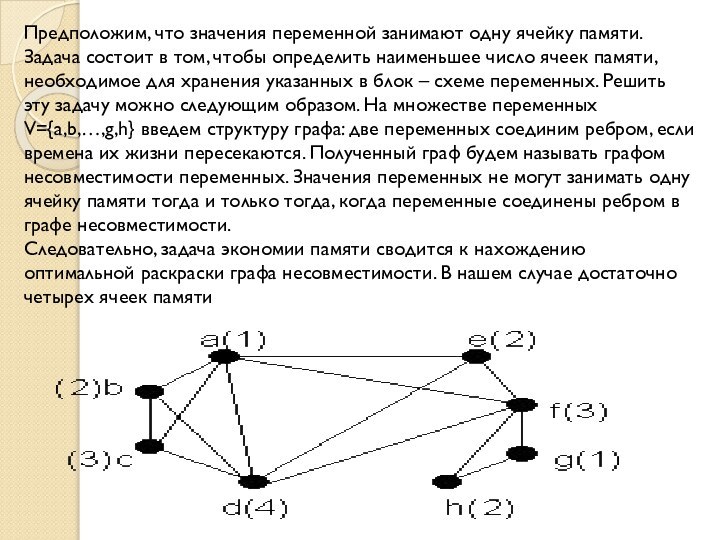
вертикальной оси отложены введенные в блок–схеме переменные, а по вертикальной «время их жизни» при вычислении значения функции φ.Слайд 13 Предположим, что значения переменной занимают одну ячейку памяти.
Задача состоит в том, чтобы определить наименьшее число ячеек
памяти, необходимое для хранения указанных в блок – схеме переменных. Решить эту задачу можно следующим образом. На множестве переменных V={a,b,…,g,h} введем структуру графа: две переменных соединим ребром, если времена их жизни пересекаются. Полученный граф будем называть графом несовместимости переменных. Значения переменных не могут занимать одну ячейку памяти тогда и только тогда, когда переменные соединены ребром в графе несовместимости.Следовательно, задача экономии памяти сводится к нахождению оптимальной раскраски графа несовместимости. В нашем случае достаточно четырех ячеек памяти