- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Интеграл и первообразная
Содержание
- 2. Содержание1. Первообразная1.1. Определение первообразной1.2. Основное свойство первообразной1.3.
- 3. 1. Первообразная 1.1. Определение первообразной Определение: Функция
- 4. 1.2 основное свойство первообразнойобщий вид первообразных. Задача
- 5. Основное свойство первообразной…Все первообразные функции f можно
- 6. Основное свойство первообразнойСвойства первообразных1) какое бы число
- 7. 1.3 три правила нахождения первообразных Правило 1.
- 8. интеграл 2.1. площадь криволинейной трапецииПусть на отрезке
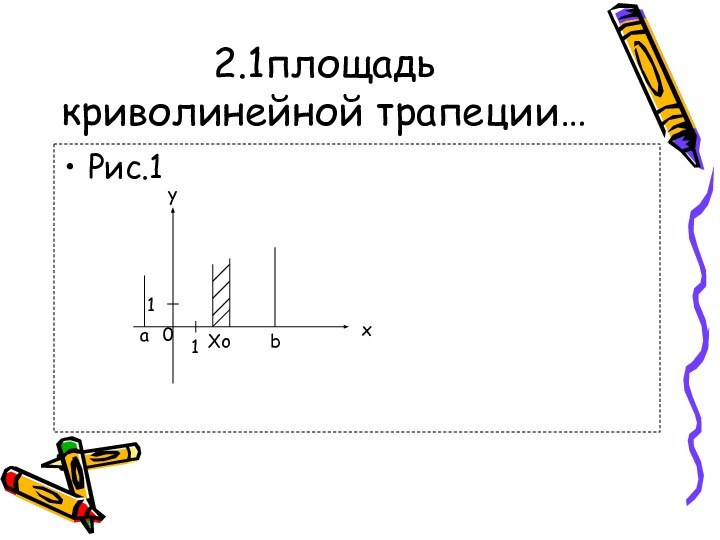
- 9. 2.1площадь криволинейной трапеции…Рис.1yx011abXo
- 10. 2.1 площади криволинейной трапеции…Пусть Хo принадлежит [a,b].
- 11. 2.1площаль криволинейной трапецииПолучили, что S есть первообразная
- 12. 2.2Интеграл. Формула Ньютона – ЛейбницаПонятие об интеграле.
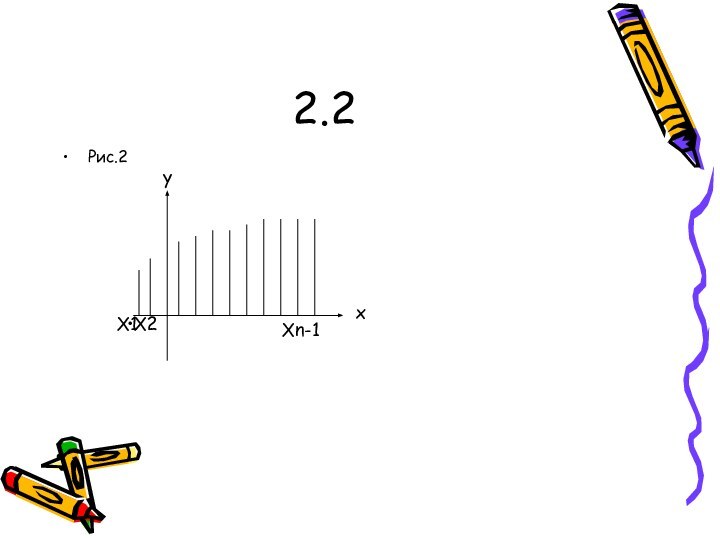
- 13. 2.2Рис.2X1X2Xn-1yx
- 14. 2.2Для любой непрерывной функции на отрезке[a,b] доказано,
- 15. 2.2Эта формула называется формулой Ньютона – Лейбница.
- 16. 1.6Таблица первообразных
- 17. Скачать презентацию
- 18. Похожие презентации
Содержание1. Первообразная1.1. Определение первообразной1.2. Основное свойство первообразной1.3. Три правила нахождения первообразной1.6. Таблица 2. Интеграл2.1. Площадь криволинейной трапеции2.2. Интеграл. Формула Ньютона – Лейбница






![Интеграл и первообразная интеграл 2.1. площадь криволинейной трапецииПусть на отрезке [a; b] оси оХ задана](/img/tmb/14/1330700/a473830985cef843f5aba1b7692ef734-720x.jpg)
![Интеграл и первообразная 2.1 площади криволинейной трапеции…Пусть Хo принадлежит [a,b]. f(x) непрерывна в Xo. Тогда](/img/tmb/14/1330700/5f152e899578a442486e9d1e6ca6f553-720x.jpg)


![Интеграл и первообразная 2.2Для любой непрерывной функции на отрезке[a,b] доказано, что Sn S к](/img/tmb/14/1330700/b6703c7f44c7f2efa078a9ead77d1699-720x.jpg)



Слайд 2
Содержание
1. Первообразная
1.1. Определение первообразной
1.2. Основное свойство первообразной
1.3. Три
правила нахождения первообразной
Интеграл. Формула Ньютона – Лейбница
Слайд 3
1. Первообразная
1.1. Определение первообразной
Определение: Функция F называется
первообразной для функции f на заданном промежутке, если для
всех х из этого промежуткаF’(x) = f(x)
Слайд 4
1.2 основное свойство первообразной
общий вид первообразных. Задача интегрирования
состоит в том, чтобы для заданной функции найти все
ее первообразные.Признак постоянства функции. Если F’(x) =0 на некотором промежутке I, то функция F – постоянна на этом промежутке.
Доказательство. Зафиксируем некоторое х0 из промежутка I. Тогда для любого числа х из такого промежутка в силу формулы Лагранжа можно указать такое число с, заключенное между х и х0 , что
F(x)-F’(c) = F’(c)(x-x0).
По условию F’(c)=0, так как с I, следовательно,
F(x)-F(x0) = 0.
Итак, для всех х из промежутка I
F(x) = F(x0),
т.е. функция F сохраняет постоянное значение.
(продолжение следует)
Слайд 5
Основное свойство первообразной…
Все первообразные функции f можно записать
с помощью одной формулы, которую называют общим видом первообразных
для функции f. Справедлива следующая теорема (основное свойство первообразных):Теорема. Любая первообразная для функции f на промежутке I может быть записана в виде
F(x) + C,
Где F(x) – одна из первообразных для функции f(x) на промежутке I, а С – произвольная постоянная.
Слайд 6
Основное свойство первообразной
Свойства первообразных
1) какое бы число ни
поставить в выражение F(x)+C вместо С, получим первообразную для
f на промежутке I.2) какую бы первообразную Ф для f на промежутке I ни взять, можно подобрать такое число С, что для всех х из промежутка I будет выполнено равенство
Ф(х) = F(x) + C.
Доказательство.
1) по условию функции F – первообразная для f на промежутке I. Следовательно, F’(x)=f(x) для любого х I, поэтому
(F(x) + C)’ = F’(x) + C’ = f(x) + 0 = f(x),
т.е. F(X) + C – первообразная для f .
2) пусть Ф(х) – одна из первообразных для функции f на том же промежутке I, т.е. Ф’(x)=f(x) для всех х I. Тогда
(Ф(х) - F(x))’ = Ф’(x) - F’(x) = f(x) - f(x) = 0
Отсюда следует в силу признака постоянства функции, что разность Ф(х) F(x) есть функция, принимающая некоторое постоянное значение С на промежутке I.
Таким образом, для всех х из промежутка I справедливо равенство Ф(х) - F(x) = C, что и требовалось доказать.
Слайд 7
1.3 три правила нахождения первообразных
Правило 1. если
F есть первообразная для f, а для G –
первообразная для g, то F+G есть первообразная для f+g.Действительно, так как F’=f и G’=g, по правилу вычисления производной суммы имеем:
(F+G)’ = F’ + G’ = f + g.
Правило 2. если F есть первообразная для f, а k – постоянная, то функция kF – первообразная для kf.
Действительно, постоянный множитель можно выносить за знак производной, поэтому:
(kF)’ = kF’ = kf.
Правило 3. если F(x) есть первообразная для f(x), а k и b – постоянные, причем k=0, то F(kx+b) есть первообразная для f(kx+b).
Действительно, по правилу вычисления производной сложной функции имеем:
( F (kx + b))’ = F’(kx + b)*k=f (kx + b)
Слайд 8
интеграл
2.1. площадь криволинейной трапеции
Пусть на отрезке [a; b]
оси оХ задана непрерывная функция f, не меняющая на
нем знака. Фигуру, ограниченную графиком этой функции, отрезком [a; b] и прямых х = а и х = b, называют криволинейной трапецией.Теорема. Если f – непрерывная и неотрицательная на отрезке [a; b] функция, a F - ее первообразная на этом отрезке, то площадь S соответствующей криволинейной трапеции равна приращению первообразной на отрезке [a; b] , т.е.
S=F(b)-F(a).
Доказательство. Рассмотрим функцию S(x), определенную на отрезке [a; b]. Если a
S’(xo) = f(xo).
Слайд 10
2.1 площади криволинейной трапеции…
Пусть Хo принадлежит [a,b]. f(x)
непрерывна в Xo. Тогда в достаточно малой окрестности в
точке Xo функцию f(x) можно считать постоянной и равной f(Xo).Тогда прирощение равно площади приближенно равно: f(x) x
S : x = f(x)
Если x 0, S : x S’(Xo)
S’(Xo) = f(Xo) т.е S - первообразная функции f в точке Xo
Слайд 11
2.1площаль криволинейной трапеции
Получили, что S есть первообразная для
f. Поэтому в силу основного свойства первообразных для всех
х [a; b] имеем:S(x) = F(x) + C,
Где С - некоторая постоянная, а F – одна из первообразных для функции f. Для нахождения С подставим х = а:
F(a) + C=S(a)=0,
Откуда С= -F(a). Следовательно,
S(x) = F(x) - F(a).
Поскольку площадь криволинейной трапеции равна S(b), подставляя х = b в формулу S(x)+F(x)-F(a), получим:
S = S(b) = F(b) - F(a).
Слайд 12
2.2Интеграл. Формула Ньютона – Лейбница
Понятие об интеграле. Пусть
функция f неотрицательна и непрерывна на отрезке [a; b],
тогда площадь S соответствующей криволинейной трапеции можно приближенно подсчитать следующим образом.Разобьем отрезок [a; b] на n отрезков одинаковой длины точками
x0 = a < x 1 < x 2 < … < x n -1 < x n = b, и пусть х = = x k – x k - 1, где k = 1, 2, …, n-1, n. На каждом из отрезков [x k-1; x k] как на основании построим прямоугольник высотой f(x k-1). сумма площадей всех таких прямоугольников (рис.2) равна:
Sn = (f(x0) + f(x1) + … + f(x n-1)).
Т.к f(x) непрерывная функция , то при x o,т.е n , то Sn S
Слайд 14
2.2
Для любой непрерывной функции на отрезке[a,b] доказано, что
Sn S к некоторому числу. Это число называют
интегралом функции .f(x)d(x), где f(x) подинтегральная функция, a – нижний предел интегрирования, b- верхний, - интеграл, x – переменная. Интеграл – это предел интегрированяи сумм. Сравнивая S= F(b) – F(a) и S= f(x)dx, можно записать