- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Интегральное исчисление.Нахождение площадей фигур в среде Mathcad
Содержание
- 2. Площадь фигурыДля нахождения площади фигуры, ограниченной кривыми,
- 3. Работа в MathcadВ среде Mathcad для определения
- 4. Формулировка заданияНайти площадь фигуры, ограниченной кривыми:
- 5. Реализация в среде MathcadДля определения пределов интегрирования
- 6. Реализация в среде MathcadЗададим обе функции:
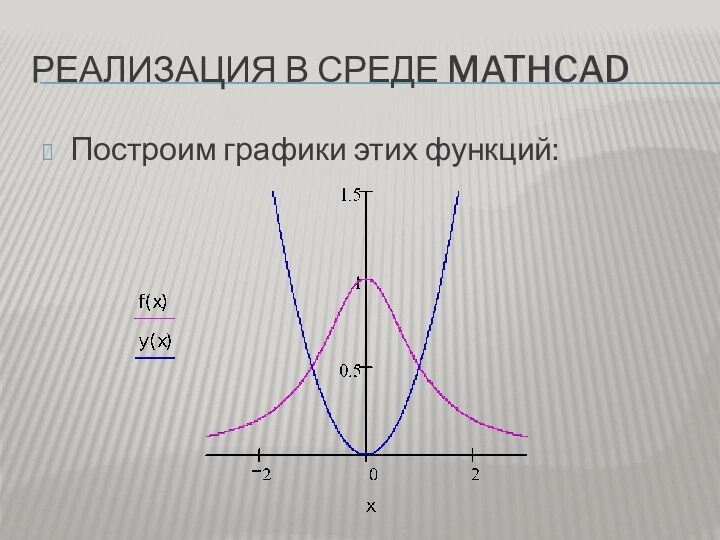
- 7. Реализация в среде MathcadПостроим графики этих функций:
- 8. Реализация в среде MathcadПо графику определилась фигура, площадь которой нужно найти:Зададим эту новую функцию в Mathcad
- 9. Реализация в среде MathcadТакже графически определились приближенные пределы интегрированияЗададим приближенное значение нижнего предела интегрирования:
- 10. Реализация в среде MathcadТочное значение нижнего предела
- 11. Реализация в среде MathcadЗададим приближенное значение верхнего предела интегрирования и найдем его точное значение:
- 12. Реализация в среде MathcadТеперь можно найти значение интеграла фигуры g(x), ограниченной линиями f(x) и y(x):
- 13. Скачать презентацию
- 14. Похожие презентации
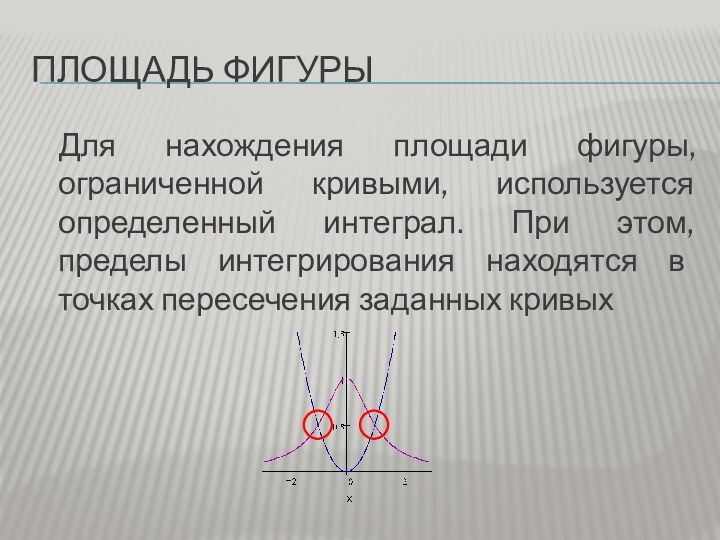
Площадь фигурыДля нахождения площади фигуры, ограниченной кривыми, используется определенный интеграл. При этом, пределы интегрирования находятся в точках пересечения заданных кривых











Слайд 3
Работа в Mathcad
В среде Mathcad для определения пределов
интегрирования используется функция root(f(x),x), а для нахождения определенного интеграла
– соответствующий шаблон на наборной панели Calculus
Слайд 5
Реализация в среде Mathcad
Для определения пределов интегрирования необходимо
будет построить графики обеих функций, графически определить приближенные значения,
а потом, используя функцию root(f(x),x), найти точные значения пределов интегрированияДля построения графиков функций, обозначим одну функцию за f(x), а вторую за y(x)