Презентация на тему История золотого сечения

делении ввел в научный обиход Пифагор, древнегреческий философ и

математик (VI в. до н.э.). Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.

Далее

Начало

в рельефе из храма фараона Сети I в Абидосе

и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

Далее

Начало

обучали своих детей при помощи геометрических фигур. Квадрат Пифагора

и диагональ этого квадрата были основанием для построения динамических прямоугольников.

Рис. 7. Динамические прямоугольники

Далее

Начало

присутствуют золотые пропорции. При его раскопках обнаружены циркули, которыми

пользовались архитекторы и скульпторы античного мира. В Помпейском циркуле (музей в Неаполе) также заложены пропорции золотого деления.

Рис. 8. Античный циркуль золотого сечения

Далее

Начало

золотое деление впервые упоминается в «Началах» Евклида. Во 2-й

книге «Начал» дается геометрическое построение золотого деления После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.

Далее

Начало

золотому делению среди ученых и художников в связи с

его применением как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи, художник и ученый, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи и Галилеем. Лука Пачоли был учеником художника Пьеро Делла Франчески, написавшего две книги, одна из которых называлась «О перспективе в живописи». Его считают творцом начертательной геометрии.

Далее

Начало

уделял изучению золотого деления. Он производил сечения стереометрического тела,

образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.

Далее

Начало

Кеплер назвал золотое сечение одним из сокровищ геометрии. Он

первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение).

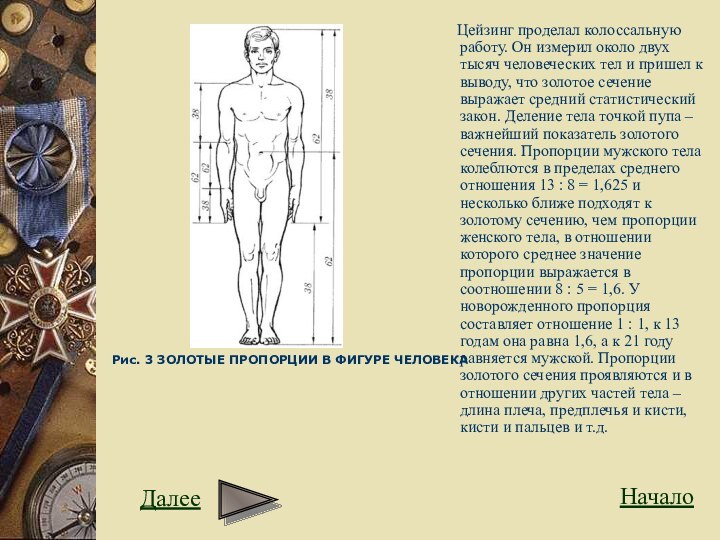
Рис. 1 Построение шкалы отрезков золотой пропорции

Кеплер называл золотую пропорцию продолжающей саму себя «Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности».

Построение ряда отрезков золотой пропорции можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд).

Если на прямой произвольной длины, отложить отрезок m, рядом откладываем отрезок M. На основании этих двух отрезков выстраиваем шкалу отрезков золотой пропорции восходящего и нисходящего рядов

Далее

Начало

пропорции превратилось в академический канон и, когда со временем

в искусстве началась борьба с академической рутиной, в пылу борьбы «вместе с водой выплеснули и ребенка». Вновь «открыто» золотое сечение было в середине XIX в. В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». С Цейзингом произошло именно то, что и должно было неминуемо произойти с исследователем, который рассматривает явление как таковое, без связи с другими явлениями. Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях «математической эстетикой».

Рис. 2 Золотые пропорции в частях тела человека

Далее

Начало

измерил около двух тысяч человеческих тел и пришел к

выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.

Рис. 3 ЗОЛОТЫЕ ПРОПОРЦИИ В ФИГУРЕ ЧЕЛОВЕКА

Далее

Начало

Наиболее подробно он разработал пропорции Аполлона Бельведерского. Подверглись исследованию

греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона, стихотворные размеры. Цейзинг дал определение золотому сечению, показал, как оно выражается в отрезках прямой и в цифрах. Когда цифры, выражающие длины отрезков, были получены, Цейзинг увидел, что они составляют ряд Фибоначчи, который можно продолжать до бесконечности в одну и в другую сторону. Следующая его книга имела название «Золотое деление как основной морфологический закон в природе и искусстве». В 1876 г. в России была издана небольшая книжка, почти брошюра, с изложением этого труда Цейзинга. Автор укрылся под инициалами Ю.Ф.В. В этом издании не упомянуто ни одно произведение живописи.
В конце XIX – начале XX вв. появилось немало чисто формалистических теории о применении золотого сечения в произведениях искусства и архитектуры. С развитием дизайна и технической эстетики действие закона золотого сечения распространилось на конструирование машин, мебели и т.д.

Далее

Начало

"Золотые" спирали широко распространены в биологическом мире.

Как отмечалось выше, рога животных растут лишь с одного конца. Этот рост осуществляется по логарифмической спирали. В книге "Кривые линии в жизни" Т. Кук исследует различные виды спиралей, проявляющихся в рогах баранов, коз, антилоп и других рогатых животных. Среди множества спиралей он выбирает "золотую" спираль ("кривую гармонического возрастания") и рассматривает ее как символ эволюции и возрастания.

Далее

Начало

закручиваются усики растений, по спирали происходит рост тканей в

стволах деревьев, по спирали расположены семечки в подсолнечнике, спиральные движения (нутации) наблюдаются при росте корней и побегов. Очевидно, в этом проявляется наследственность организации растений, а ее корни следует искать на клеточном и молекулярном уровне.

Далее

Начало

обратили внимание на целесообразность форм и поверхностей раковин: внутренняя

поверхность гладкая, наружная - рифленая. Внутри покоится тело моллюска - внутренняя поверхность должна быть гладкой. Наружные ребра увеличивают жесткость раковины и, таким образом, повышают ее прочность. Форма раковин поражает своим совершенством и экономичностью средств, затраченных на ее создание. Идея спирали в раковинах выражена не приближенно, а в совершенной геометрической форме, в удивительно красивой, "отточенной" конструкции.

Далее

Начало

формирующих конические раковины, отвечает числам Фибоначчи. Так, раковины фораминифер

имеют 13 частей, раковины шпорцевой улитки - 8, количество камер раковины наутилуса - 34, тело наутилоидей делится на 13 частей, раковина гигантской тридакны собрана в 5 складок. Число ребер ископаемой раковины брахиопод равно 34. Такое же количество ребер имеют крохотные раковины тектакулитов. По краям пятнистой раковины ципреи из Индийского океана расположены мелкие зубцы, количество которых равно 21. Из приведенных примеров видно, что конструкции раковин многих ископаемых и современных моллюсков предпочитают числа 5, 8, 13, 21, 34.

Далее

Начало

мы смотрим в зеркало, мы наблюдаем в нем свое

отражение - это пример "зеркальной" симметрии. Зеркальное отражение - это пример так называемого "ортогонального" преобразования, изменяющего ориентацию.

Далее

Начало

природе обратили внимание еще пифагорейцы в связи с развитием

ими учения о гармонии. Установлено, что в природе наиболее распространены два вида симметрии - "зеркальная" и "лучевая" (или "радиальная") симметрии. "Зеркальной" симметрией обладает бабочка, листок или жук (Рис.а) и часто такой вид симметрии называется "симметрией листка" или "билатеральной симметрией". К формам с лучевой симметрией относятся гриб, ромашка, сосновое дерево (Рис.б) и часто такой вид симметрии называется "ромашко-грибной" симметрией.

 

Природные формы с "билатеральной" (а) и "радиальной" (b) симметрией

Далее

Начало