Презентация на тему Как находить площадь многоугольника

площадей, вывести формулу площади прямоугольника; закрепить изученные формулы в

ходе решения задач
Развитие логического мышления
Привитие интереса к предмету геометрии

вычислять площади фигур
4. Понятие площади
5. Площадь прямоугольника
6. Закрепление
7. Самостоятельная

работа
8. Проверка самостоятельной работы
9. Итоги урока
10. Домашнее задание

проведены две прямые, параллельные двум сторонам треугольника. На какие

фигуры разбивается этими прямыми данный треугольник?
2.

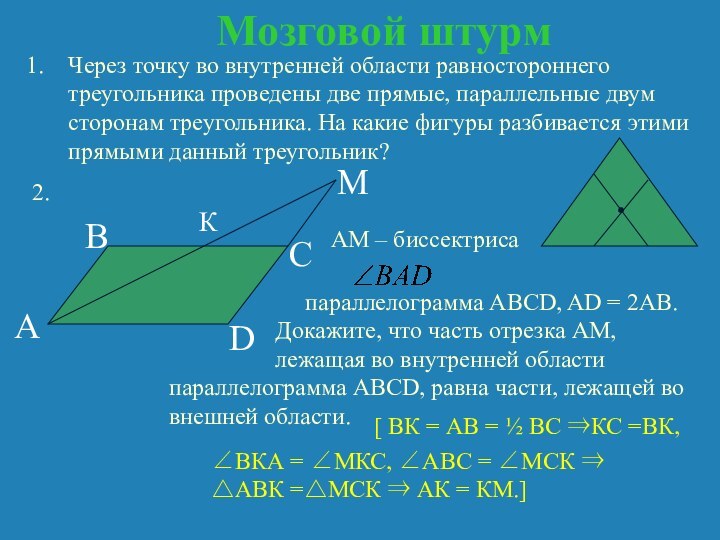
AM – биссектриса

параллелограмма ABCD, AD = 2AB.

A

B

C

D

M

Докажите, что часть отрезка АМ, лежащая во внутренней области

параллелограмма ABCD, равна части, лежащей во внешней области.

[ ВК = АВ = ½ ВС ⇒КС =ВК,

К

∠ВКА = ∠МКС, ∠АВС = ∠МСК ⇒ △АВК =△МСК ⇒ АК = КМ.]

•

равна 25 м² , площадь сада – 6 соткам.С

понятием «площадь» и формулами для вычисления площадей некоторых фигур вы уже встречались. Какие это фигуры?

[ прямоугольник: S = ab; круг: S= ]

Площадь поверхности стен в помещении нужно знать, например, для того, чтобы рассчитать необходимое для их покрытия количество обоев, краски или кафеля.

Важно ли в жизни уметь измерять и вычислять площади фигур? Как вы думаете, для чего, например?

частности, чтобы определить, как станет испаряться из заполненного водохранилища

вода.

Площадь поверхности дороги нужно знать, чтобы рассчитать необходимое для её покрытия количества асфальта.

той части плоскости, которую занимает многоугольник. Измерение площадей проводится

с помощью выбранной единицы измерения аналогично измерению длин отрезков. За единицу измерения площадей принимают квадрат, сторона которого равна единице измерения отрезков. Если за единицу измерения отрезков принят сантиметр, то за единицу измерения площадей принимают квадрат со стороной 1 см. Такой квадрат называют квадратным сантиметром ( см² )

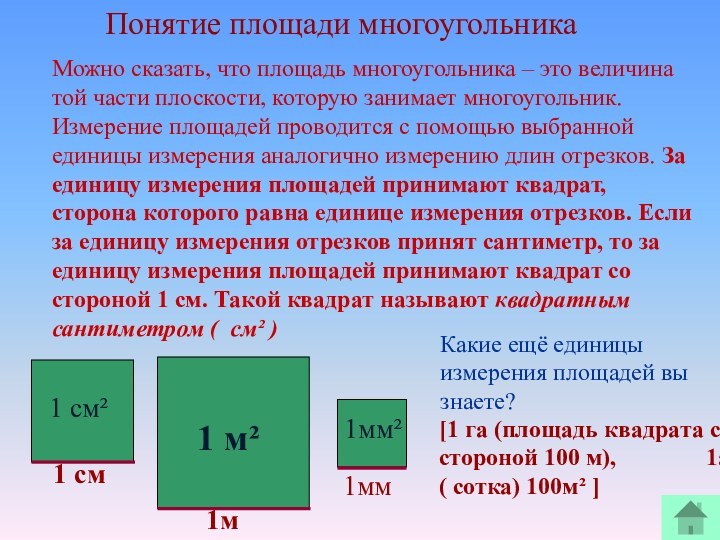
1 см

1 см²

1м

1мм

1мм²

Какие ещё единицы измерения площадей вы знаете?

[1 га (площадь квадрата со стороной 100 м), 1а ( сотка) 100м² ]

Понятие площади многоугольника

1 м²

выражается положительным числом. Это число показывает, сколько раз единица

измерения площади и её части укладываются в данном многоугольнике.

S = 6см²

1 см²

1см

S ≈ 2,24 см²

измеряют лишь некоторые связанные с многоугольником отрезки, а затем

вычисляют площадь по определённым формулам. Вывод этих формул основан на следующих свойствах площадей

1. Равные многоугольники имеют равные площади.

2. Если многоугольник составлен из нескольких многоугольников,то его площадь равна сумме площадей этих многоугольников.

3. Площадь квадрата равна квадрату его стороны

S = S₁ + S₂+ S₃

a

a

S = a²

S₁

S₂

S₃

F₁

F₂

сторон.
S
S
b
a
b
b

С другой стороны

( a + b )² = S + S + a² + b² . a² + 2ab + b² = 2S + a² + b².

a²

b²

a

a

Дано: прямоугольник, a, b – стороны, S – площадь.

Доказать: S = ab

Доказательство:
1) Достроим прямоугольник до квадрата со стороной а + b.

По свойству (3.) его площадь равна ( a + b )² .

S = ab

S

параллелограмма.

( ВН – высота)

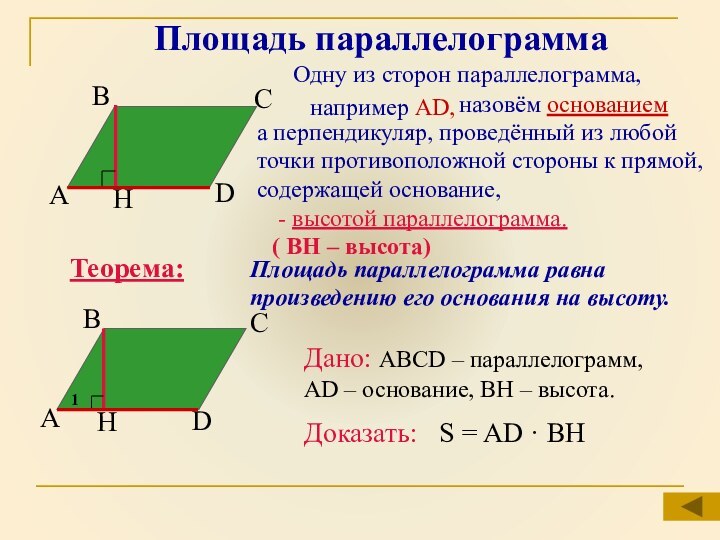
Теорема:

Площадь параллелограмма равна произведению его основания на высоту.

А

В

С

D

H

1

Дано: ABCD – параллелограмм, AD – основание, ВН – высота.

Доказать: S = AD · BH

например AD,

назовём основанием

а перпендикуляр, проведённый из любой точки противоположной стороны к прямой, содержащей основание,

состоит из △ABH и трапеции HBCD,
а прямоугольник HBCK

– из трапеции HBCD и △DCK. Так как △ABH = △DCK ( по гипотенузе (АВ = DC) и острому углу ( ∠1 = ∠2 как соответственные при AB∥CD ) ).
Значит, , а , но ВС = AD. ⇒
или S = ah, где а – основание, h – высота.

S = ah

СН – высота
Теорема:
Площадь треугольника равна половине произведения

основания на высоту.

Доказать:

Доказательство:

Достроим до параллелограмма.

D

Следствия:

Площадь прямоугольного треугольника равна половине произведения его катетов.
Если высоты двух треугольников равны, то их площади относятся, как основания.

S
[ CD = 30 : 2 = 15;

15·10=150 ]

А

В

C

D

M

Найдите

[ т.к △СМЕ = △DAE, то

= Q ]

E

2 АВ, то АВ =

х, AD = 2x. ( х + 2х)·2 = 48, х = 8.

АВ = 8 см, AD = 16 см

S = 8·16 S = 128 см²

б) △АВМ = △NCM, ⇒

II вариант
а) АВ = х, ВС = х + 5, (х + х + 5)·2 = 46, 2х + 5 = 23, х = 9

АВ = 9 см, ВС = 14 см

S = 9 · 14, S = 126 см²

б)△FCE =△ADE,⇒

Перечислить свойства площадей
3. Чему равна площадь прямоугольника?
4. Чему равна

площадь параллелограмма?

5. Чему равна площадь треугольника?