- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Краткая запись условия задач. Схемы задач.
Содержание
- 2. Алгоритм решения задачи:1.Читаю задачу.2.Понимаю текст.3. Фиксирую условие
- 3. У Оли было 7 красных воздушных шариков
- 4. Подбери задачу к схеме: 1. Мама испекла
- 5. Объясни, чем отличаются эти задачи, реши
- 6. 1. На берёзе сидело
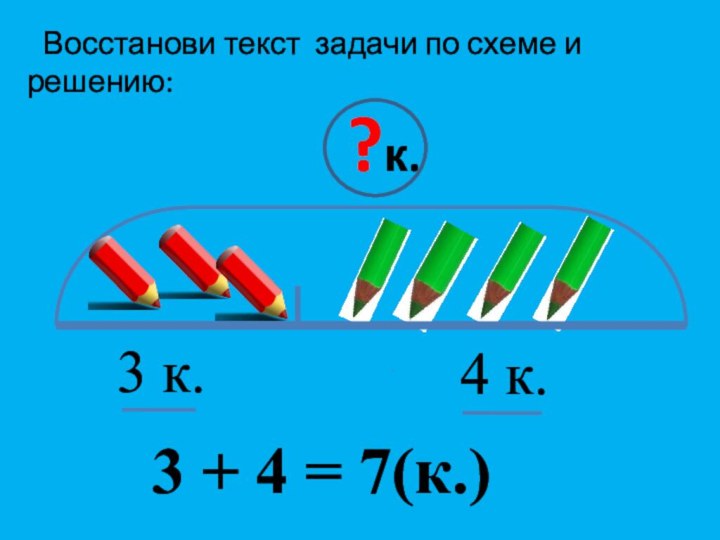
- 7. ?к.3 к. 4 к. 3 + 4
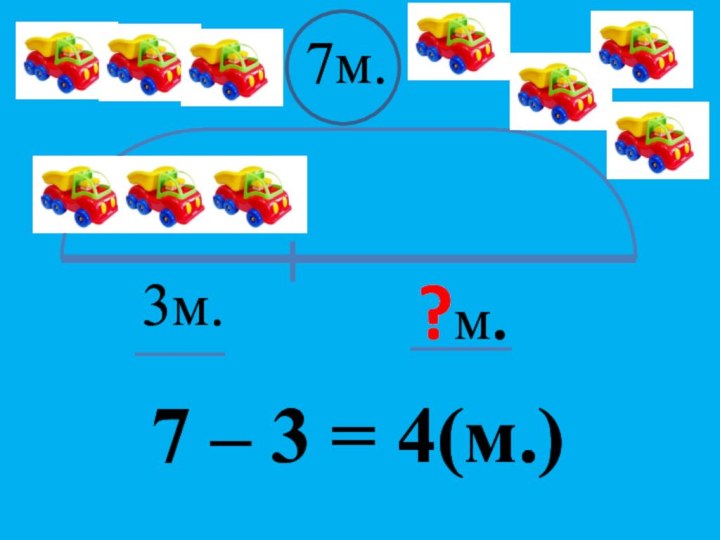
- 8. 3м.?м.7м. 7 – 3 = 4(м.)
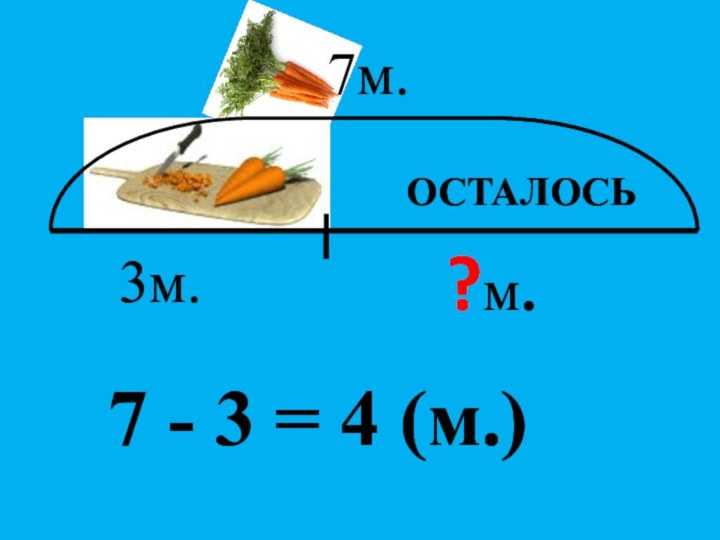
- 9. ?м.3м.7м.ОСТАЛОСЬ7 - 3 = 4 (м.)
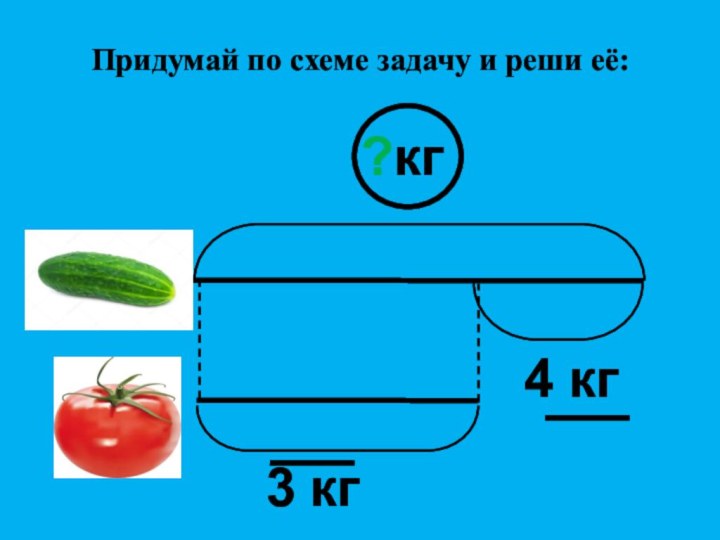
- 10. 3 кг4 кг?кг Придумай по схеме задачу
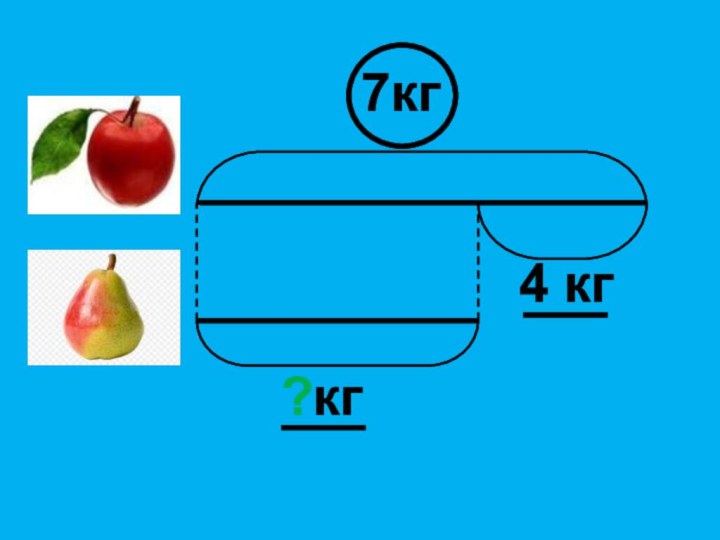
- 11. ?кг4 кг7кг
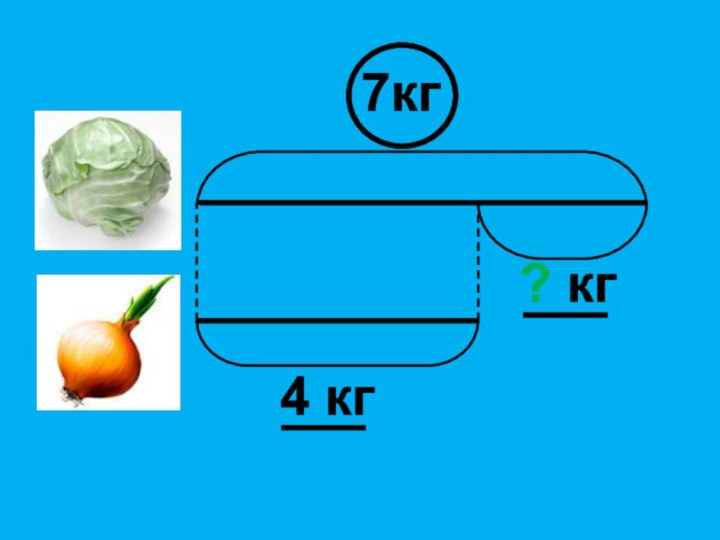
- 12. 4 кг? кг7кг
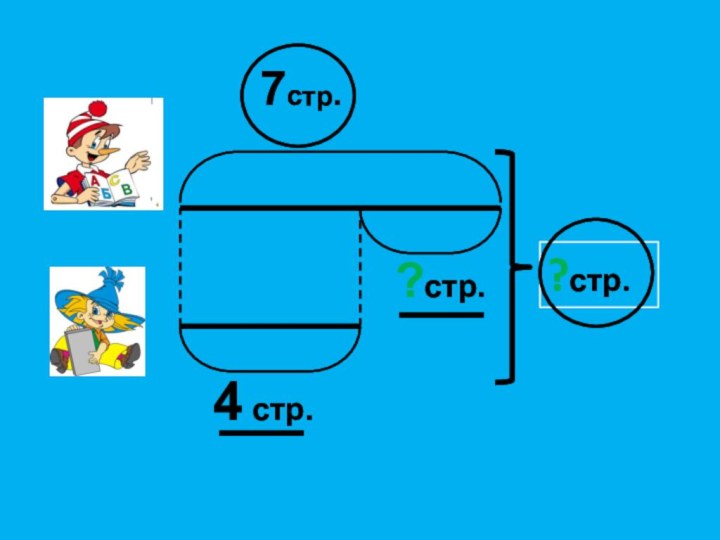
- 13. 4 стр.?стр.7стр.?стр.
- 14. Составь схемы к задачам: 1. Кот Матроскин поймал
- 15. Что такое текстовая задача?Текстовая задача есть описание
- 16. Роль текстовых задач в начальном обучении математике
- 18. Способы решения текстовых задач. Решить
- 19. Этапы решение текстовой задачи арифметическим
- 20. Приемы анализа задач: Основной традиционный прием анализа
- 21. Приемы работы с задачей: - Реши задачу
- 23. Скачать презентацию
- 24. Похожие презентации
Алгоритм решения задачи:1.Читаю задачу.2.Понимаю текст.3. Фиксирую условие схемы.4. Пишу формулы.5. Вычисляю, записываю ответ.6. Возвращаюсь к тексту задачи, делаю проверку.










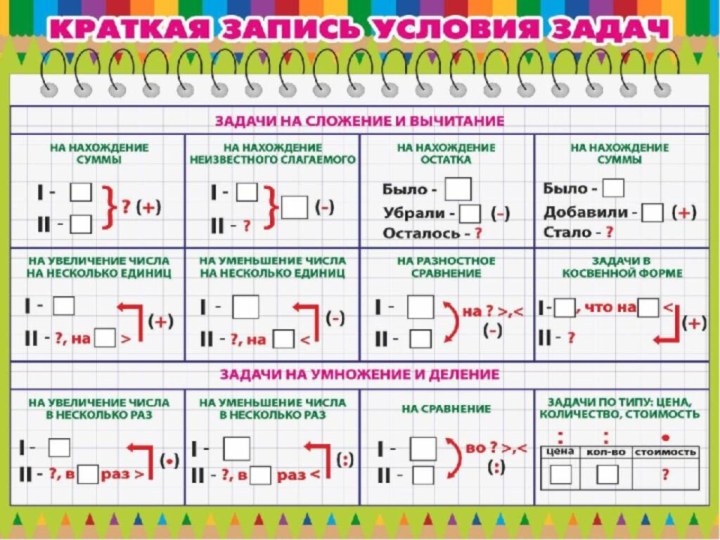

Слайд 2
Алгоритм решения задачи:
1.Читаю задачу.
2.Понимаю текст.
3. Фиксирую условие схемы.
4.
Пишу формулы.
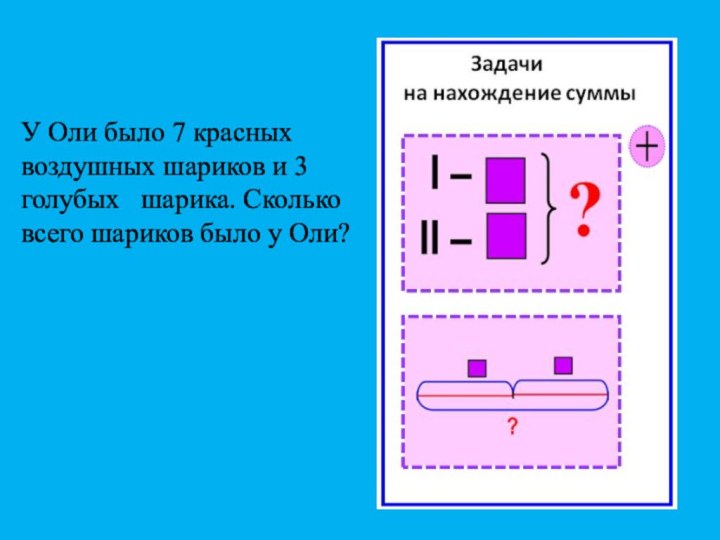
делаю проверку.Слайд 3 У Оли было 7 красных воздушных шариков и
3 голубых шарика. Сколько всего шариков было у
Оли?
Слайд 4
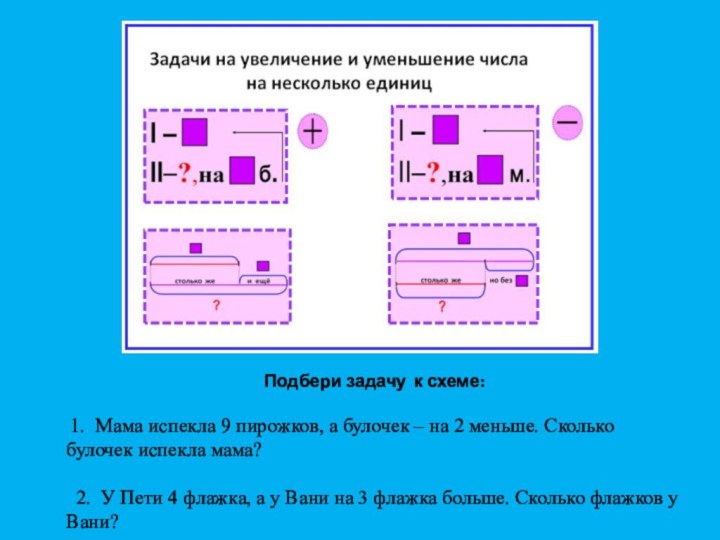
Подбери задачу к схеме:
1. Мама испекла 9
пирожков, а булочек – на 2 меньше. Сколько булочек
испекла мама?2. У Пети 4 флажка, а у Вани на 3 флажка больше. Сколько флажков у Вани?
.
Слайд 5
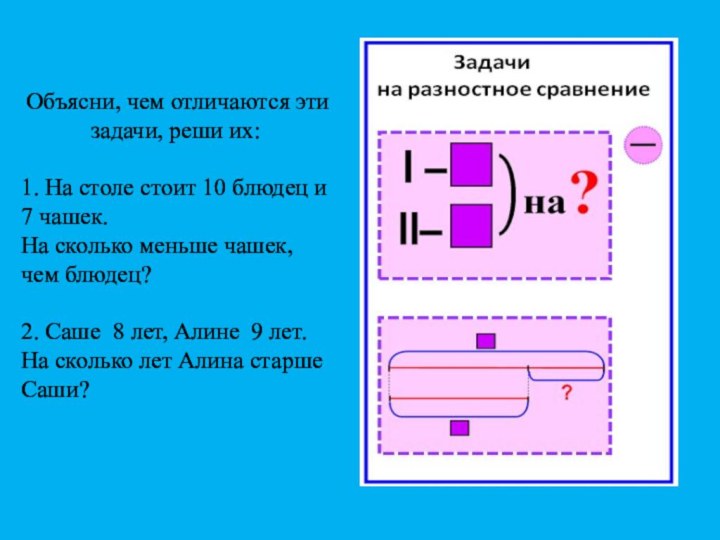
Объясни, чем отличаются эти задачи, реши их:
1.
На столе стоит 10 блюдец и 7 чашек.
На
сколько меньше чашек, чем блюдец? 2. Саше 8 лет, Алине 9 лет. На сколько лет Алина старше Саши?
Слайд 6
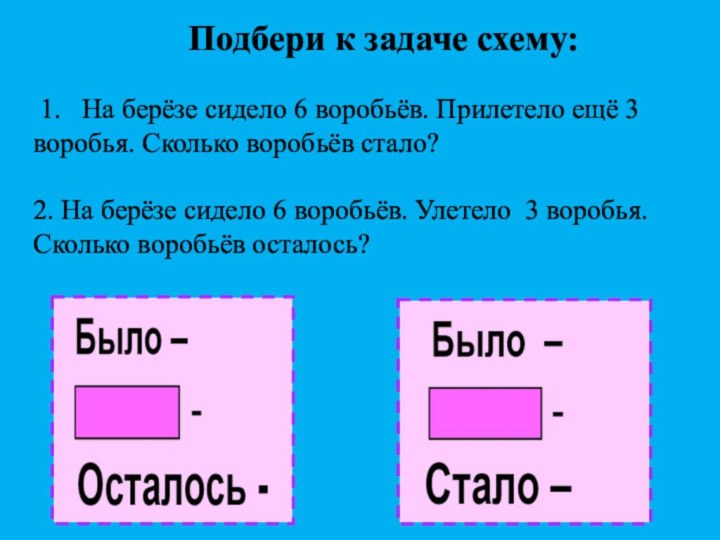
1. На берёзе сидело 6
воробьёв. Прилетело ещё 3 воробья. Сколько воробьёв стало?
2. На
берёзе сидело 6 воробьёв. Улетело 3 воробья. Сколько воробьёв осталось? Подбери к задаче схему:
Слайд 14
Составь схемы к задачам:
1. Кот Матроскин поймал 10 карасей,
а кот Леопольд на 3 карася меньше. Сколько карасей
поймал кот Леопольд?2. Кот Матроскин поймал 7 карасей, а кот Леопольд на 3 карася больше. Сколько карасей поймал кот Леопольд?
Слайд 15
Что такое текстовая задача?
Текстовая задача есть описание некоторой
ситуации (ситуаций) на естественном языке с требованием дать количественную
характеристику какого-либо компонента этой ситуации, установить наличие или отсутствие некоторого отношения между ее компонентами или определить вид этого отношения.
Слайд 16
Роль текстовых задач в начальном обучении математике
Решая задачи, учащиеся приобретают новые математические знания, готовятся
к практической деятельности.Задачи способствуют развитию их логического мышления. Большое значение имеет решение задач и в воспитании личности учащегося.
Поэтому важно, чтобы учитель имел глубокие представления о текстовой задаче, о ее структуре, умел решать такие задачи различными способами. Существуют простые и составные задачи.
Задачи, которые решаются в одно действие называются простыми задачи, решающиеся в два и более – составные.
Слайд 17
Из чего состоит текстовая задача?
Любая
текстовая задача состоит из двух частей: условия и требования
(вопроса).В условии сообщаются сведения об объектах и некоторых величинах, характеризующих данные объекты, об известных и неизвестных значениях этих величин, об отношениях между ними.
Требования задачи – это указание того, что нужно найти. Оно может быть выражено предложением в повелительной (Найти площадь прямоугольника) или вопросительной форме (Чему равна площадь прямоугольника?).
Слайд 18
Способы решения текстовых задач.
Решить задачу – это
значит через логически верную последовательность действий и операций с
имеющимися в задаче явно или косвенно числами, величинами, отношениями выполнить требование задачи (ответить на ее вопрос).В качестве основных в математике различают арифметические и алгебраические способы решения задач. При арифметическом способе ответ на вопрос задачи находится в результате выполнения арифметических действий над числами.
Слайд 19 Этапы решение текстовой задачи арифметическим способом
Восприятие и анализ содержания задачи.
Поиск и составление плана решения
задачи.Выполнение плана решения. Формулировка вывода о выполнении требования задачи (ответа на вопрос задачи).
Проверка решения и устранение ошибок, если они есть. Формулировка окончательного вывода о выполнении требования задачи или ответа на вопрос задачи.
Слайд 20
Приемы анализа задач:
Основной традиционный прием анализа задач
– разбор от вопроса и от числовых данных.
Разбор
задачи от вопроса – это суждение, которое состоит в том, чтобы подобрать два числовых значения одной или разных величин таким образом, чтобы дать ответ на вопрос задачи. Одно из значений или оба могут быть неизвестными. Для их нахождения подбираются два других, и так продолжается процесс подбора, пока не приходим к известным числовым значениям величин.В результате такого разбора учащиеся устанавливают зависимость между числовыми значениями величин, расчленяют ее на простые задачи и составляют план ее решения.
Слайд 21
Приемы работы с задачей:
- Реши задачу другим
способом
- Составь и реши обратную задачу
- Составление аналогичной задачи
с измененными данными. - Измени вопрос так, чтобы задача решалась в одно (два) действие и др.
- Решение задач с недостающими или лишними данными.
- Запись двух решений на доске – одного верного и другого неверного.
- Изменение условий задачи так, чтобы задача решалась другим действием.
- Закончить решение задачи.