- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Как построить график функции y=f(x+L)+m, если известен график функции y=f(x)
Содержание
- 2. ТЕМА УРОКА Как построить график функции y=f(x+L)+m, если известен график функции y=f (x).
- 3. Цель урока: Научиться строить график функции y=f (x + L) +m.
- 4. Устная работа Назовите координаты вершины
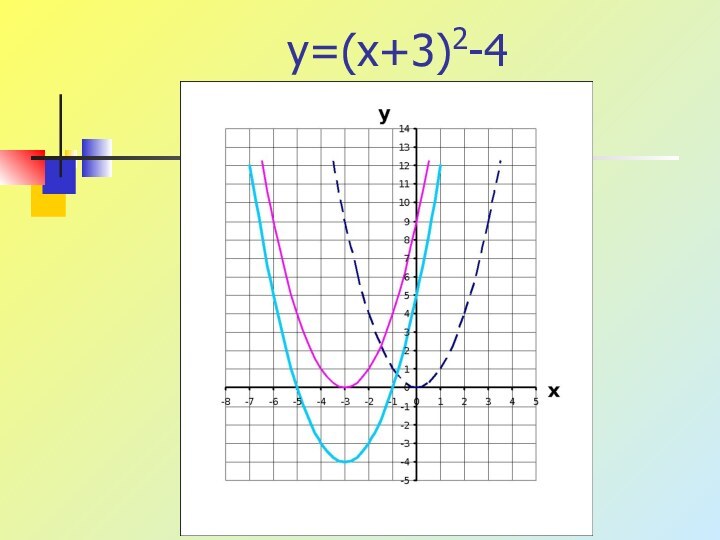
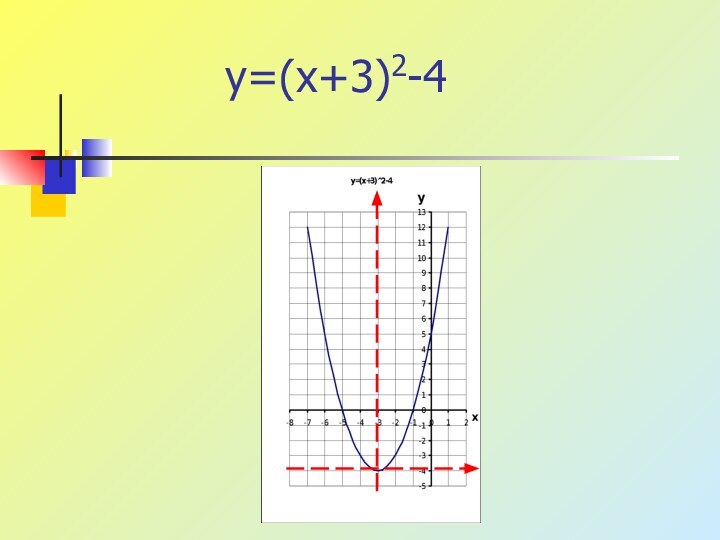
- 5. y=(x+3)2-4
- 6. y=(x+3)2-4
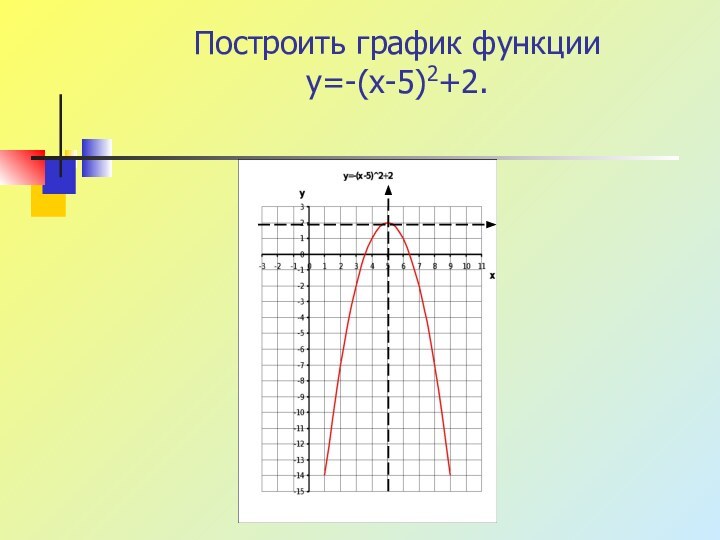
- 7. Построить график функции y=-(x-5)2+2.
- 8. Алгоритм 1 1. Построить график функции y=f(x).2.
- 9. Алгоритм 21.Перейдем к новой системе координат, проведя
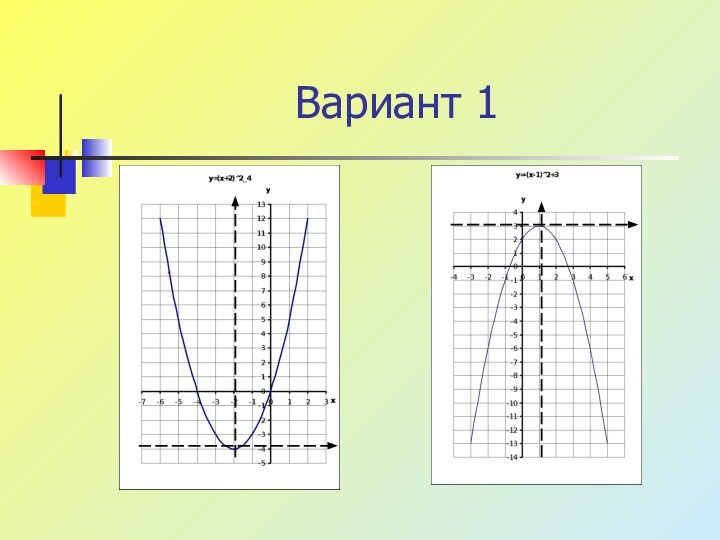
- 10. Самостоятельная работа Вариант 1
- 11. Вариант 1
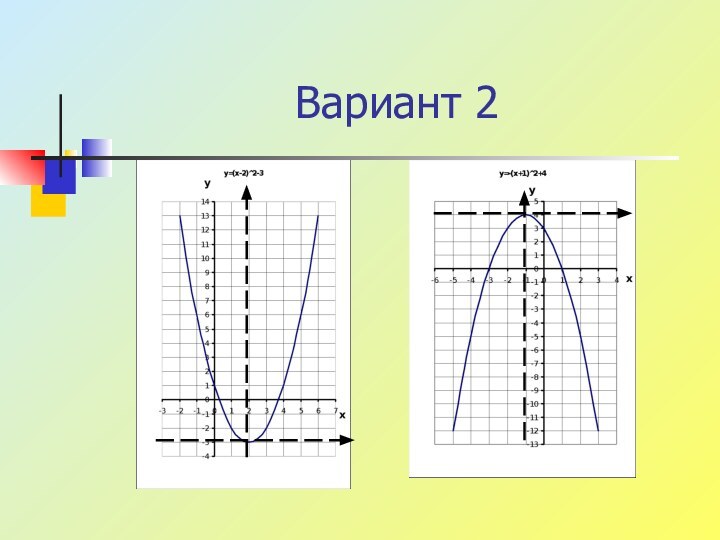
- 12. Вариант 2
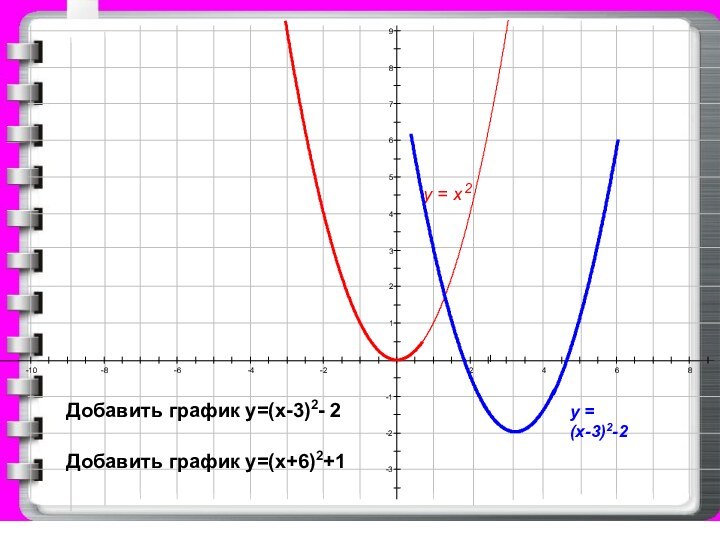
- 13. 987654321-1-2-3-10-8-6-4-22468у = х2у = (х-3)2-2Добавить график у=(х-3)2- 2Добавить график у=(х+6)2+1
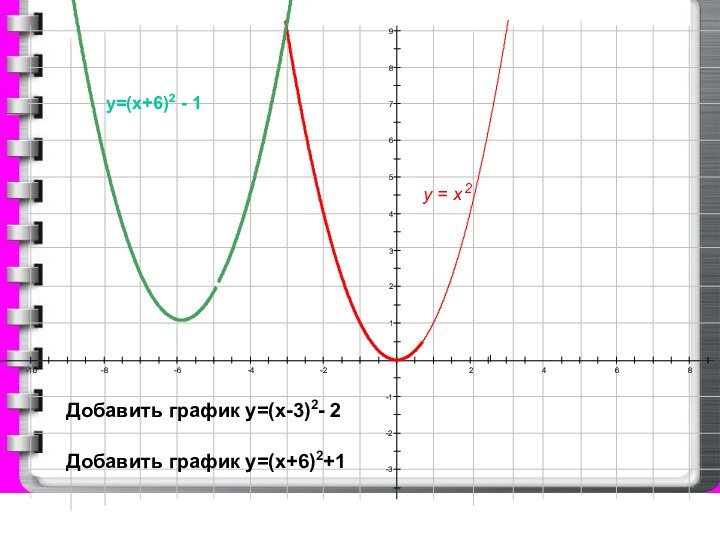
- 14. 987654321-1-2-3-10-8-6-4-22468у = х2Добавить график у=(х-3)2- 2Добавить график у=(х+6)2+1у=(х+6)2 - 1
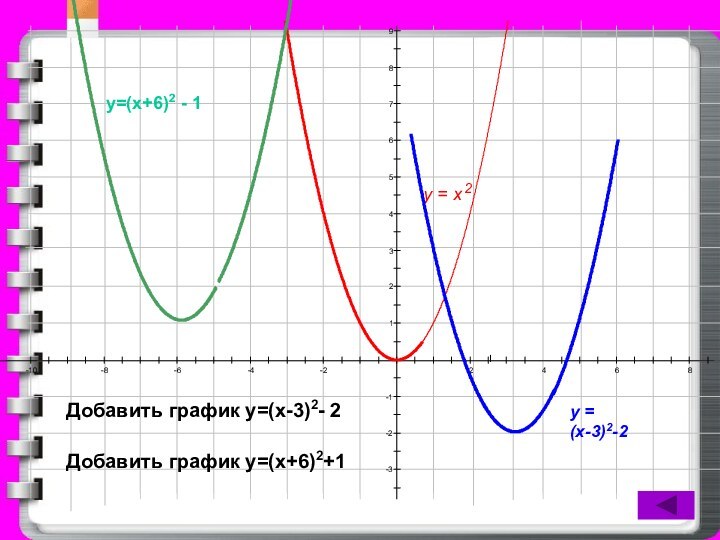
- 15. 987654321-1-2-3-10-8-6-4-22468у = х2у = (х-3)2-2Добавить график у=(х-3)2- 2Добавить график у=(х+6)2+1у=(х+6)2 - 1
- 16. g(x) = f(x) + aГg получается из
- 17. g(x) = f(x) + aГg получается из
- 18. g(x) = f(x) + aГg получается из
- 19. g(x) = f(x + a)Гg получается из
- 20. g(x) = f(x + a)Гg получается из
- 21. g(x) = f(x + a)Гg получается из
- 22. Домашнее задание§ 10 № 10.36(в, г);№ 10.41(а);№ 10.35(а; б).
- 23. Скачать презентацию
- 24. Похожие презентации
ТЕМА УРОКА Как построить график функции y=f(x+L)+m, если известен график функции y=f (x).









Слайд 4
Устная работа
Назовите координаты вершины параболы, направление её
ветвей, уравнение оси симметрии:
а) y=x2 – 1; б) y=-2x2 + 5; в) y=(x-2)2; г) y=1/2(x+2)2.
Слайд 8
Алгоритм 1
1. Построить график функции y=f(x).
2. Осуществить параллельный
перенос графика функции y=f(x) вдоль оси x на l
L l единиц масштаба влево, если L>0, и вправо, если L<0.3. Осуществить параллельный перенос полученного на втором шаге графика вдоль оси y на l m l единиц масштаба вверх, если m>0, и вниз, если m<0.
Слайд 9
Алгоритм 2
1.Перейдем к новой системе координат, проведя вспомогательные
прямые x=-L, y=m (т.е. выбрав началом новой системы точку(-L;m)).
2.
В новой системе координат построить график функции y=f (x).
Слайд 10
Самостоятельная работа
Вариант 1
Вариант 2
1. y=(x+2)2-4
1. y=(x-2)2-32. y=-(x-1)2+3 2. y=-(x+1)2+4
Слайд 13
9
8
7
6
5
4
3
2
1
-1
-2
-3
-10
-8
-6
-4
-2
2
4
6
8
у =
х
2
у = (х-3)2-2
Добавить график у=(х-3)2- 2
Добавить
график у=(х+6)2+1
Слайд 14
9
8
7
6
5
4
3
2
1
-1
-2
-3
-10
-8
-6
-4
-2
2
4
6
8
у =
х
2
Добавить график у=(х-3)2- 2
Добавить график у=(х+6)2+1
у=(х+6)2
Слайд 15
9
8
7
6
5
4
3
2
1
-1
-2
-3
-10
-8
-6
-4
-2
2
4
6
8
у =
х
2
у = (х-3)2-2
Добавить график у=(х-3)2- 2
Добавить
график у=(х+6)2+1
у=(х+6)2 - 1
Слайд 16
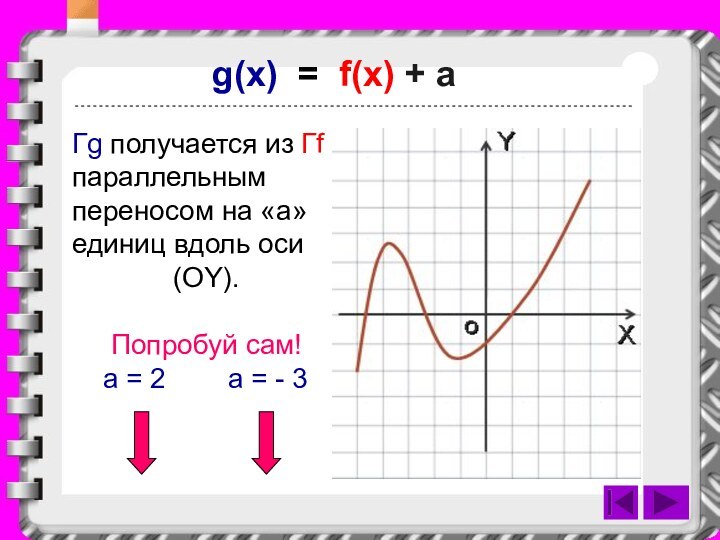
g(x) = f(x) + a
Гg получается из Гf
параллельным переносом на «a» единиц вдоль оси
(OY). Попробуй сам!
a = 2 a = - 3
Слайд 17
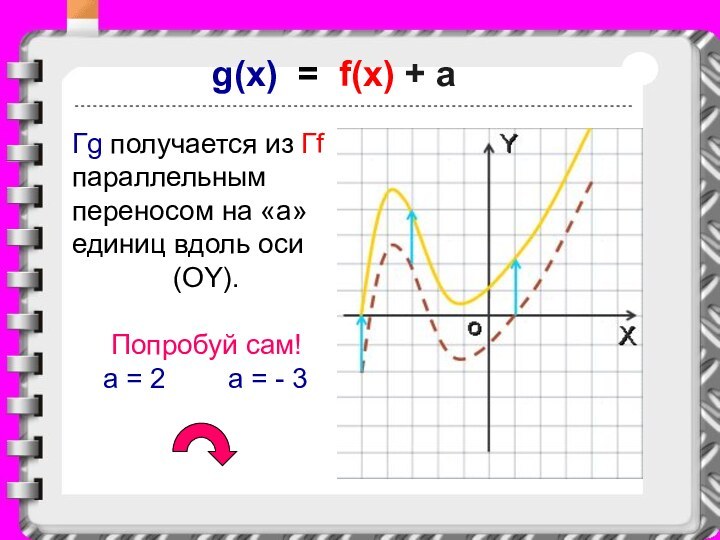
g(x) = f(x) + a
Гg получается из Гf
параллельным переносом на «a» единиц вдоль оси
(OY). Попробуй сам!
a = 2 a = - 3
Слайд 18
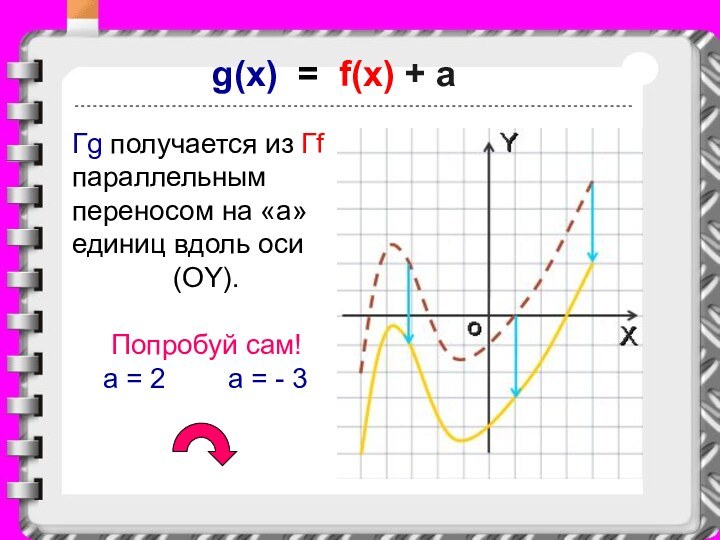
g(x) = f(x) + a
Гg получается из Гf
параллельным переносом на «a» единиц вдоль оси
(OY). Попробуй сам!
a = 2 a = - 3
Слайд 19
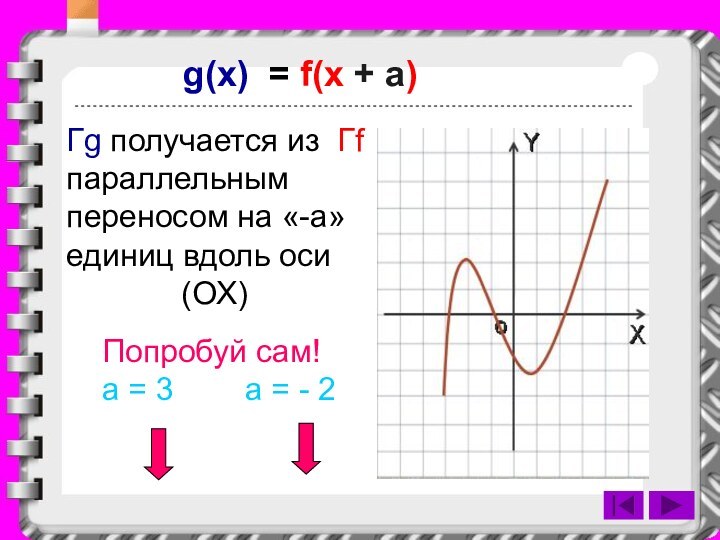
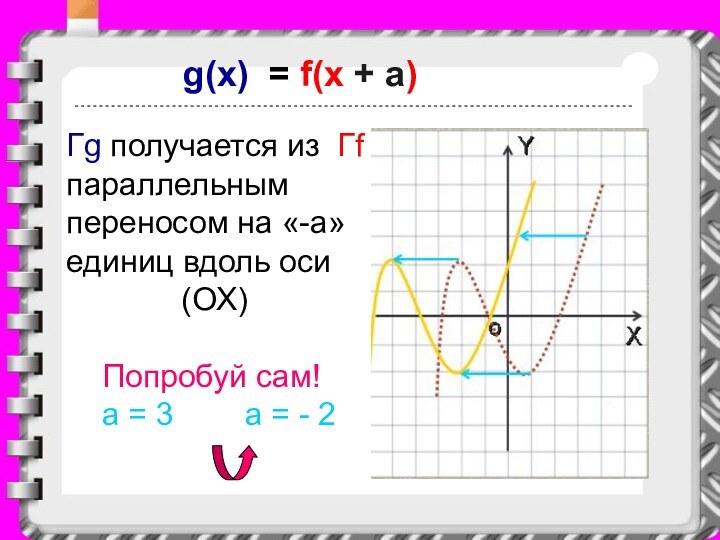
g(x) = f(x + a)
Гg получается из Гf
параллельным переносом на «-a» единиц вдоль оси
(ОХ)Попробуй сам!
a = 3 a = - 2
Слайд 20
g(x) = f(x + a)
Гg получается из Гf
параллельным переносом на «-a» единиц вдоль оси
(ОХ)Попробуй сам!
a = 3 a = - 2
Слайд 21
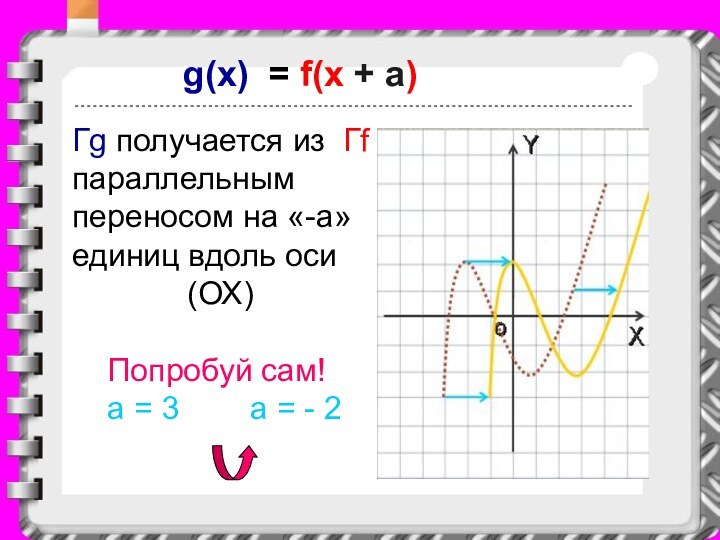
g(x) = f(x + a)
Гg получается из Гf
параллельным переносом на «-a» единиц вдоль оси
(ОХ)Попробуй сам!
a = 3 a = - 2





























