- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Классификация систем нечеткой логики
Содержание
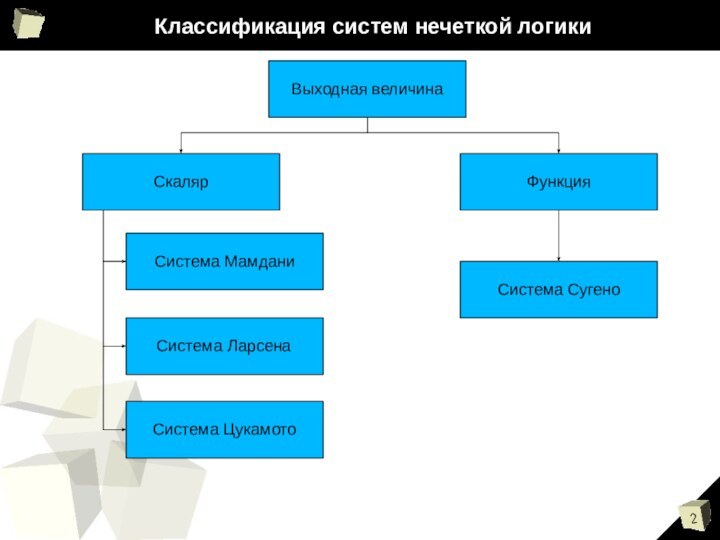
- 2. Классификация систем нечеткой логикиВыходная величинаФункцияСистема МамданиСистема СугеноСистема ЛарсенаСистема ЦукамотоСкаляр
- 3. Система нечеткой логики МамданиВпервые как обособленная система
- 4. Система нечеткой логики МамданиФункция, описывающая зависимость между
- 5. Система нечеткой логики МамданиПример графического отображения зависимости
- 6. Система нечеткой логики МамданиПример: регулирование уровня воды
- 7. Система нечеткой логики ЛарсенаИногда данную систему рассматривают
- 8. Система нечеткой логики ЦукамотоДанная система использует свой
- 9. Система нечеткой логики СугеноВ иностранной литературе эту
- 10. Скачать презентацию
- 11. Похожие презентации
Классификация систем нечеткой логикиВыходная величинаФункцияСистема МамданиСистема СугеноСистема ЛарсенаСистема ЦукамотоСкаляр


Слайд 2
Классификация систем нечеткой логики
Выходная величина
Функция
Система Мамдани
Система Сугено
Система Ларсена
Система
Цукамото
Слайд 3
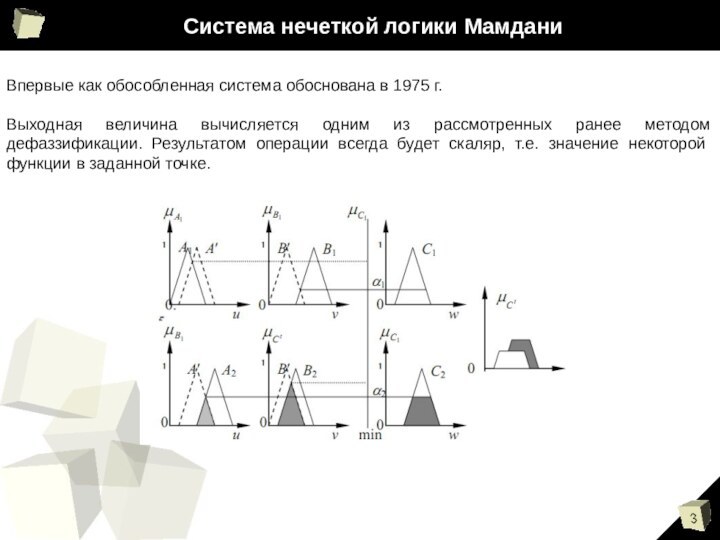
Система нечеткой логики Мамдани
Впервые как обособленная система обоснована
в 1975 г.
Выходная величина вычисляется одним из рассмотренных ранее
методом дефаззификации. Результатом операции всегда будет скаляр, т.е. значение некоторой функции в заданной точке.
Слайд 4
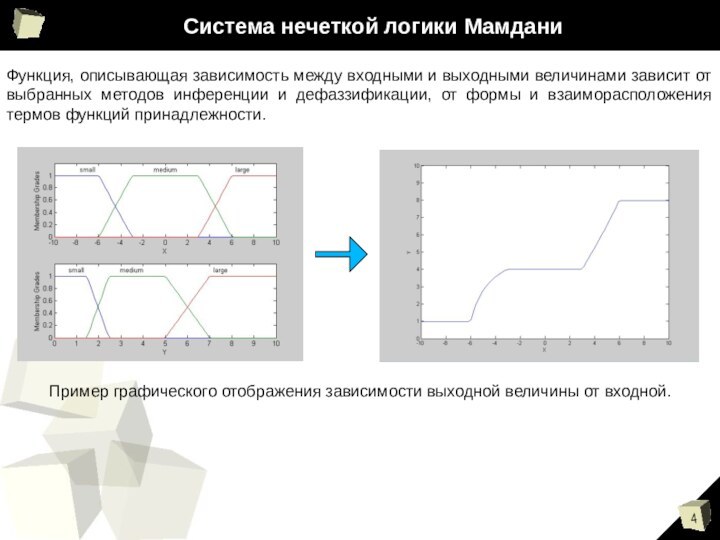
Система нечеткой логики Мамдани
Функция, описывающая зависимость между входными
и выходными величинами зависит от выбранных методов инференции и
дефаззификации, от формы и взаиморасположения термов функций принадлежности.Пример графического отображения зависимости выходной величины от входной.
Слайд 5
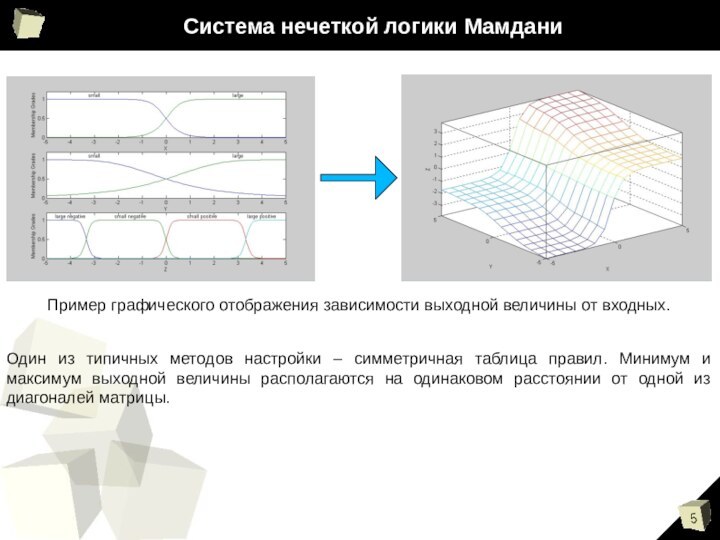
Система нечеткой логики Мамдани
Пример графического отображения зависимости выходной
величины от входных.
Один из типичных методов настройки – симметричная
таблица правил. Минимум и максимум выходной величины располагаются на одинаковом расстоянии от одной из диагоналей матрицы.
Слайд 6
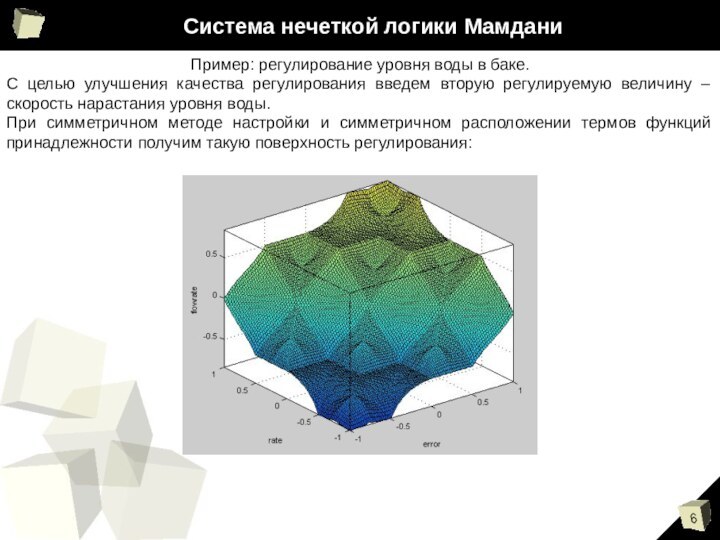
Система нечеткой логики Мамдани
Пример: регулирование уровня воды в
баке.
С целью улучшения качества регулирования введем вторую регулируемую величину
– скорость нарастания уровня воды.При симметричном методе настройки и симметричном расположении термов функций принадлежности получим такую поверхность регулирования:
Слайд 7
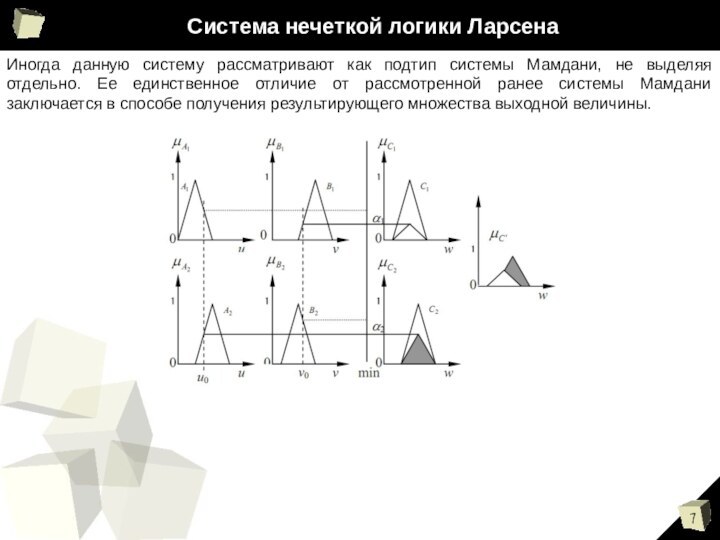
Система нечеткой логики Ларсена
Иногда данную систему рассматривают как
подтип системы Мамдани, не выделяя отдельно. Ее единственное отличие
от рассмотренной ранее системы Мамдани заключается в способе получения результирующего множества выходной величины.
Слайд 8
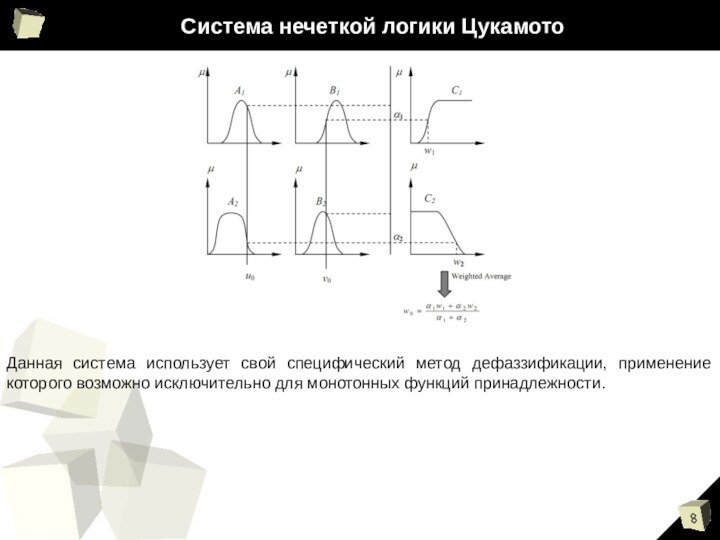
Система нечеткой логики Цукамото
Данная система использует свой специфический
метод дефаззификации, применение которого возможно исключительно для монотонных функций
принадлежности.
Слайд 9
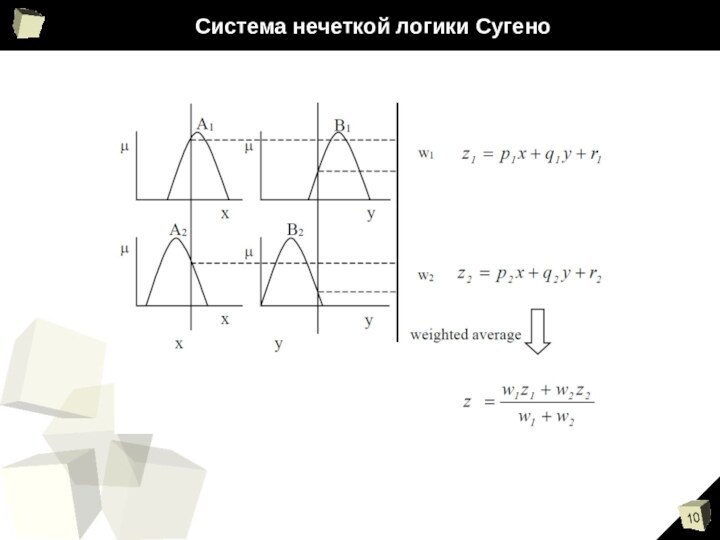
Система нечеткой логики Сугено
В иностранной литературе эту систему
также называют TSK, как аббревиатуру фамилий трех ее основоположников
– Такаги, Сугено, Канг, сформулировавших принципы работы такой системы в 1985-1988 гг.Принципиальное отличие от рассмотренных ранее систем заключается в методике инференции. Предыдущие системы работают на основе правил:
ЕСЛИ х∈А ТО y∈В
В основе системы Сугено лежит иной принцип:
ЕСЛИ х∈A ТО y=f(x)
То есть, на выходе такой системы мы имеем некоторую функцию, например, полиномиальную.