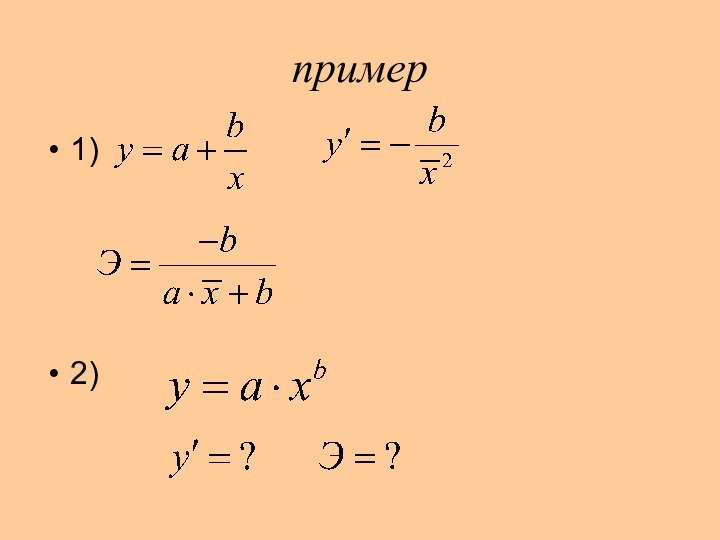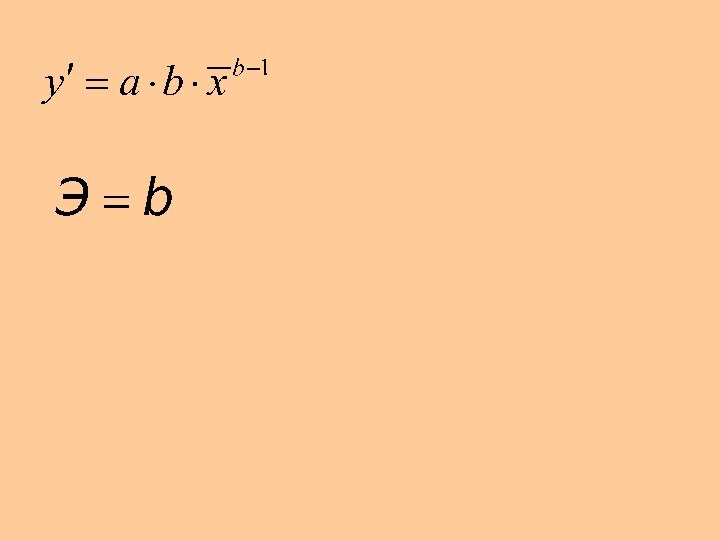Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Коэффициент эластичности

Содержание

пример1)2)
коэффициент эластичности показывает, на сколько процентов в среднем по совокупности изменится пример1)2) Прогнозное значение определяется путем подстановки в уравнение примерВыполнить, по уравнению регрессии y=280+5,6x, прогноз заработной платы y при прогнозном значении средняя стандартная ошибка прогноза : доверительный интервал прогноза Нелинейная регрессия. Корреляция для нелинейной регрессии. Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций Различают два класса нелинейных регрессий: 1) регрессии, нелинейные относительно включенных в анализ Примером нелинейных регрессий по переменным могут служить следующие функции:- полиномы разных степеней К нелинейным регрессиям по оцениваемым параметрам относятся функции:- степенная - показательная - экспоненциальная Нелинейная регрессия определяется, как в линейной регрессии, методом наименьших квадратов (МНК). в параболе второй степени ,заменяя переменные , получим двухфакторное уравнение линейной регрессии: для полинома k-го порядка получим линейную модель множественной регрессии с k объясняющими переменными: В уравнении равносторонней гиперболы – делаем замену z=1/x,получаем линейное уравнение Для степенной модели линеаризация производится путём логарифмирования обеих частей уравнения Для показательной модели линеаризация производится также с помощью логарифмирования обеих Корреляция для нелинейной регрессии. Величина данного показателя находится в границах: проверка существенности в целом уравнения нелинейной регрессии осуществляется с помощью F-критерия Фишера
Слайды презентации

Слайд 2 пример
1)




2)





пример1)2)

Слайд 3

Слайд 4 Прогнозное значение определяется

Прогнозное значение определяется путем подстановки в уравнение регрессии

путем подстановки в уравнение регрессии
соответствующего (прогнозного)

значения .








Слайд 5 пример
Выполнить, по уравнению регрессии y=280+5,6x, прогноз заработной платы

примерВыполнить, по уравнению регрессии y=280+5,6x, прогноз заработной платы y при прогнозном

y при прогнозном значении среднедушевого прожиточного минимума x, составляющем

127% от среднего уровня (xp=6700).

Слайд 6
средняя стандартная ошибка прогноза :


средняя стандартная ошибка прогноза :

Слайд 7 доверительный интервал прогноза


доверительный интервал прогноза

Слайд 8 Нелинейная регрессия.
Корреляция для нелинейной регрессии.



Нелинейная регрессия. Корреляция для нелинейной регрессии.

Слайд 9 Если между экономическими явлениями существуют нелинейные соотношения, то

Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций

они выражаются с помощью соответствующих нелинейных функций

Слайд 10 Различают два класса нелинейных регрессий:
1) регрессии, нелинейные

Различают два класса нелинейных регрессий: 1) регрессии, нелинейные относительно включенных в

относительно включенных в анализ объясняющих переменных, но линейные по

оцениваемым параметрам;
2) регрессии, нелинейные по оцениваемым параметрам.

Слайд 11 Примером нелинейных регрессий по переменным могут служить следующие

Примером нелинейных регрессий по переменным могут служить следующие функции:- полиномы разных

функции:
- полиномы разных степеней



- равносторонняя гипербола - .




Слайд 12
К нелинейным регрессиям по оцениваемым параметрам относятся функции:
-

К нелинейным регрессиям по оцениваемым параметрам относятся функции:- степенная - показательная - экспоненциальная

степенная

- показательная

- экспоненциальная



Слайд 13
Нелинейная регрессия определяется, как в линейной регрессии, методом

Нелинейная регрессия определяется, как в линейной регрессии, методом наименьших квадратов (МНК).

наименьших квадратов (МНК).


Слайд 14 в параболе второй степени ,

заменяя переменные ,

в параболе второй степени ,заменяя переменные , получим двухфакторное уравнение линейной регрессии:


получим двухфакторное уравнение линейной регрессии:




Слайд 15 для полинома k-го порядка



получим линейную модель множественной

для полинома k-го порядка получим линейную модель множественной регрессии с k объясняющими переменными:

регрессии с k объясняющими переменными:



Слайд 16 В уравнении равносторонней гиперболы –



делаем замену z=1/x,
получаем

В уравнении равносторонней гиперболы – делаем замену z=1/x,получаем линейное уравнение

линейное уравнение

y=a+bz


Слайд 17 Для степенной модели

линеаризация производится

Для степенной модели линеаризация производится путём логарифмирования обеих частей

путём логарифмирования обеих частей уравнения

с помощью замены

получаем линейное уравнение



Слайд 18 Для показательной модели

линеаризация производится

Для показательной модели линеаризация производится также с помощью логарифмирования

также с помощью логарифмирования обеих частей уравнения

с помощью

замены

получаем линейное уравнение



Слайд 19 Корреляция для нелинейной регрессии.




Величина данного показателя находится

Корреляция для нелинейной регрессии. Величина данного показателя находится в границах:

в границах:

чем ближе к единице, тем теснее связь рассматриваемых признаков.



  • Имя файла: koeffitsient-elastichnosti.pptx
  • Количество просмотров: 106
  • Количество скачиваний: 0
- Предыдущая Интеллектуально-познавательная игра по физике Лучшие из Пяти
Следующая - Обыкновенные дроби

Похожие презентации

Единицы измерения длины. Сантиметр Единицы измерения длины. Сантиметр 105
Симметрия в природе Симметрия в природе 132
Производная в графиках ЕГЭ Производная в графиках ЕГЭ 161
Презентация к внеклассному мероприятию по теме День программиста Презентация к внеклассному мероприятию по теме День программиста 167
uberi lishnyuyu figuru uberi lishnyuyu figuru 100
Технология развития критического мышления Технология развития критического мышления 148
Путешествие в мир математики Путешествие в мир математики 124
Аксонометрические проекции Аксонометрические проекции 92
Решение задач. план-конспект урока по математике (3 класс) по теме Решение задач. план-конспект урока по математике (3 класс) по теме 120
Памятка по оформлению краткой записи к задачам 1-2 класс Памятка по оформлению краткой записи к задачам 1-2 класс 129
Деление с остатком Деление с остатком 134
Леонтий Филиппович Магницкий Леонтий Филиппович Магницкий 82
Проценты в школьном курсе математики Проценты в школьном курсе математики 133
Числа Числа 125
Все действия с одночленами Все действия с одночленами 108
Число как результат измерения величины Число как результат измерения величины 108
Умножение одночлена. Возведение одночлена в степень Умножение одночлена. Возведение одночлена в степень 113
порядок действий презентация к уроку по математике порядок действий презентация к уроку по математике 121
Многогранники в архитектуре Многогранники в архитектуре 113
Движение Движение 187
Противоположные числа Противоположные числа 169
Презентация к уроку по теме Смешанные числа Презентация к уроку по теме Смешанные числа 104
Треугольники. Первый признак равенства Треугольники. Первый признак равенства 122
В гостях у сказки презентация к уроку по математике (младшая группа) по теме В гостях у сказки презентация к уроку по математике (младшая группа) по теме 128
Дробно-рациональные уравнения Дробно-рациональные уравнения 97
ТАНГРАМ ТАНГРАМ 103
Знакомство с геометрическими фигурами Урок по математике в 1 классе по УМК Начальная школа 21 века план-конспект урока по математике (1 класс) по теме Знакомство с геометрическими фигурами Урок по математике в 1 классе по УМК Начальная школа 21 века план-конспект урока по математике (1 класс) по теме 78
Вычисления с многозначными числами Вычисления с многозначными числами 103
Решение задач методическая разработка по математике (3 класс) Решение задач методическая разработка по математике (3 класс) 144
Движение скорость, время, расстояние 4 класс Движение скорость, время, расстояние 4 класс 134