- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Комбинаторика. Решение комбинаторных задач
Содержание
- 2. Комбинаторика. Решение комбинаторных задач. Творческий проект учащихся
- 3. Комбинаторика ПеречислительнаяСтруктурнаяЭкстремальная ВероятностнаяТопологическая
- 4. Цель работы - изучить основные понятия комбинаторики
- 5. Что изучает комбинаторика?Комбинаторика изучает количества комбинаций, подчиненных
- 6. Основные понятия и некоторые формулы комбинаторики.Перестановками называют
- 7. Размещениями называют комбинации, составленные из n различных
- 8. Сочетаниями называют комбинации, составленные из n
- 9. Факториал n!n! =1∙2 ∙3 ∙4 ∙5 ∙… ∙n
- 10. П р а в и л о
- 11. ЗадачиПример 1. У сборщика имеется 3 конусных
- 12. Самостоятельная работа1. В ящике имеется 50 одинаковых
- 13. Дерево вероятности
- 14. Дерево вероятностиЗадача: даны
- 15. Применение комбинаторных задачДерево вероятностиДерево заболеваемости ОРВИ школьниковДерево системы дополнительного образования школьниковДерево производственных показателей
- 16. Скачать презентацию
- 17. Похожие презентации
Комбинаторика. Решение комбинаторных задач. Творческий проект учащихся 6 Б класса Караваевой Алины и Поповой Карины.Научный руководитель: Китаева И.В.














Слайд 4 Цель работы - изучить основные понятия комбинаторики и
способы решения некоторых комбинаторных задач
Что изучает комбинаторика?
Основные понятия и
некоторые формулыЗадачи
Дерево вероятности
Применение комбинаторных задач в жизни.
Слайд 5
Что изучает комбинаторика?
Комбинаторика изучает количества комбинаций, подчиненных определенным
условиям, которые можно составить из элементов, безразлично какой природы,
заданного конечного множества. При непосредственном вычислении вероятностей часто используют формулы комбинаторики. Приведем наиболее употребительные из них.
Слайд 6
Основные понятия и некоторые формулы комбинаторики.
Перестановками называют комбинации,
состоящие из одних и тех же n различных элементов
и отличающиеся только порядком их расположения. Число всех возможных перестановокPn = n! где n! = 1 * 2 * 3 ... n.
Слайд 7 Размещениями называют комбинации, составленные из n различных элементов
по m элементов, которые отличаются либо составом элементов, либо
их порядком. Число всех возможных размещенийAmn = n (n - 1)(n - 2) ... (n - m + 1).
Слайд 8
Сочетаниями называют комбинации, составленные из n различных элементов
по m элементов, которые отличаются хотя бы одним элементом.
Число сочетанийС mn = n! / (m! (n - m)!)
Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством
Amn = PmC mn.
Слайд 10 П р а в и л о
с у м м ы. Если некоторый объект А
может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами.П р а в и л о п р о и з в е д е н и я. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана mn способами.
Слайд 11
Задачи
Пример 1. У сборщика имеется 3 конусных и
7 эллиптических валиков. Сборщик взял один валик, а затем
второй. Найти вероятность того, что первый из взятых валиков — конусный, а второй — эллиптический.Р е ш е н и е. Вероятность того, что первый валик окажется конусным (событие A),
Р (А) = 3 / 10. Вероятность того, что второй валик окажется эллиптическим (событие В), вычисленная в предположении, что первый валик — конусный, т. е. условная вероятность
РA (В) = 7 / 9. По теореме умножения, искомая вероятность
Р (АВ) = Р (А) РA (В) = (3 / 10) * (7 / 9) = 7 / 30. Заметим, что, сохранив обозначения, легко найдем: Р (В) = 7 / 10, РB (А) = 3 / 9, Р (В) РB (А) = 7 / 30, что наглядно иллюстрирует справедливость равенства (***).
Слайд 12
Самостоятельная работа
1. В ящике имеется 50 одинаковых деталей,
из них 5 окрашенных. Наудачу вынимают одну деталь. Найти
вероятность того, что извлеченная деталь окажется окрашенной. Отв. р = 0,1.2. Брошена игральная кость. Найти вероятность того, что выпадет четное число очков. Отв. р = 0,5.
3. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5. Отв. р = 0,81.
4. В мешочке имеется 5 одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв: о, п, р, с, т. Найти вероятность того, что на вынутых по одному и расположенных "в одну линию" кубиков можно будет прочесть слово "спорт". 0тв. р = 1 / 120.
5. На каждой из шести одинаковых карточек напечатана одна из следующих букв: а, т, м, р, с, о. Карточки тщательно перемешаны. Найти вероятность того, что на четырех, вынутых по одной и расположенных "в одну линию" карточках можно будет прочесть слово "трос". Отв. p = 1 / A46 = 1 / 360.
Слайд 14
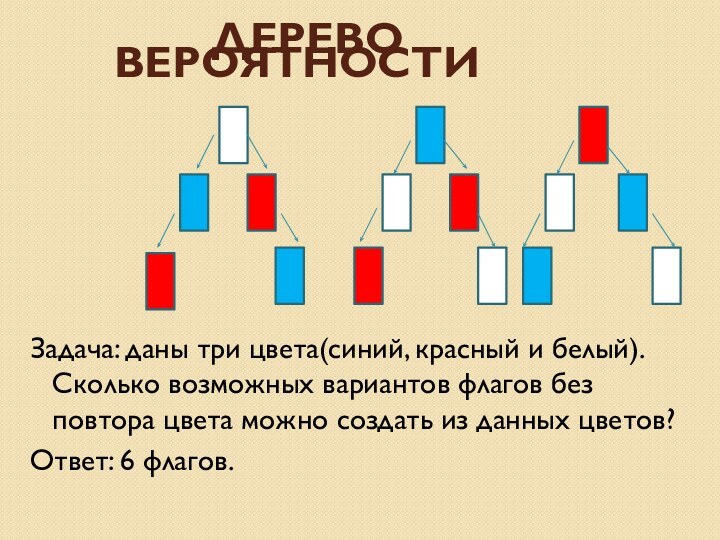
Дерево вероятности
Задача: даны три
цвета(синий, красный и белый). Сколько возможных вариантов флагов без
повтора цвета можно создать из данных цветов?Ответ: 6 флагов.