C
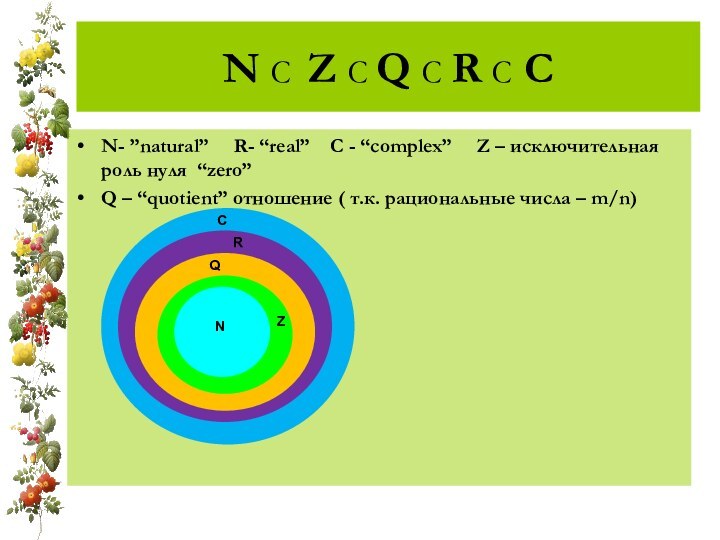
N- ”natural” R- “real” C -
“complex” Z – исключительная роль нуля “zero”Q – “quotient” отношение ( т.к. рациональные числа – m/n)
C
R
Q
Z
N
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть






C
R
Q
Z
N
Например: i, 2i, -0,3i – чисто мнимые числа.
3i +13i=(3+13)i = 16i
3i·13i = (3·13) (i·i)=39i2=-39
ПРАВИЛА АРИФМЕТИЧЕСКИХ ОПЕРАЦИЙ
10 ai+bi=(a+b)i 20 a(bi)=(ab)i
30 (ai)(bi)=abi2= -ab 40 0i =0
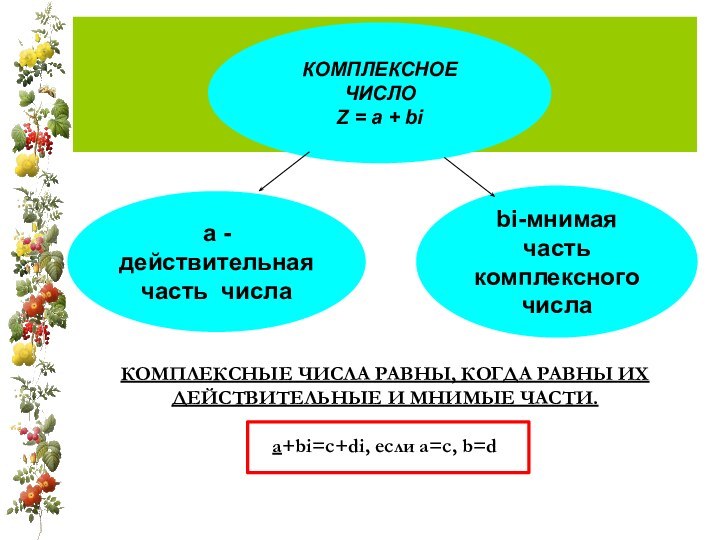
а - действительная часть числа
bi-мнимая часть комплексного числа