применить это новое понятие на практике
Потренироваться в решении заданий
с функциональными уравнениями и с построениями графиковЗакрепить пройденный материал по производным
Заинтересовать учащихся, привлечь их внимание к данной теме


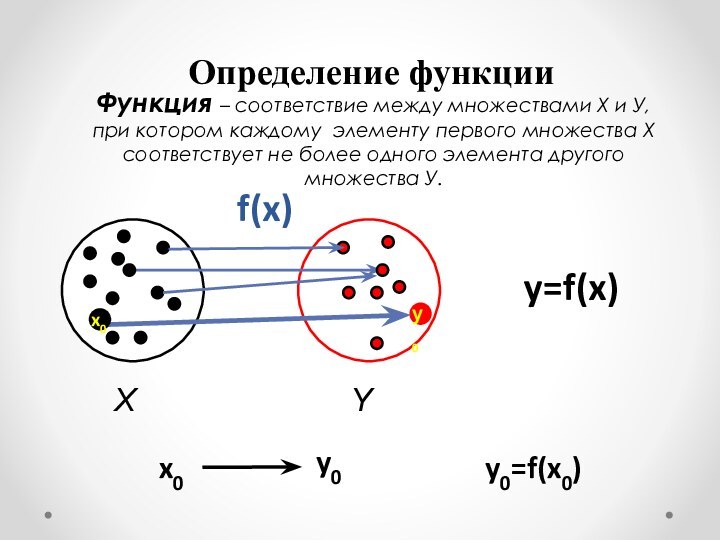
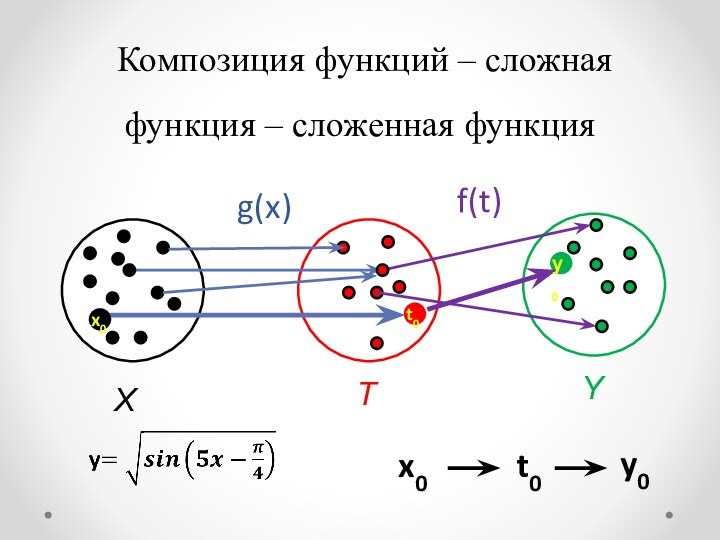

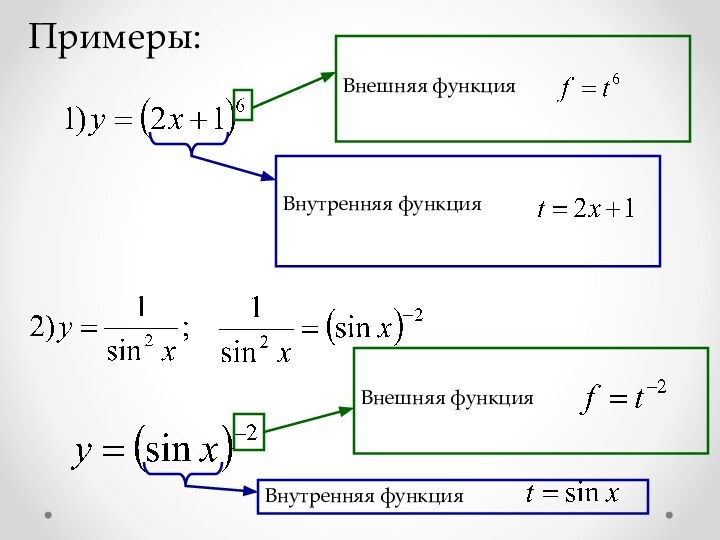
=(f∘g)(h(x))==f(g(h(x))) ,[f∘(g∘h)](x)=f[(g∘h)(x)]==f(g(h(x))) Распределительный закон распадается на два](/img/tmb/13/1261599/fa4d0fde166382646e3019640796314d-720x.jpg)