подмножество ,
Инфиксная
форма записи бинарного отношенияa T b =
.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть





















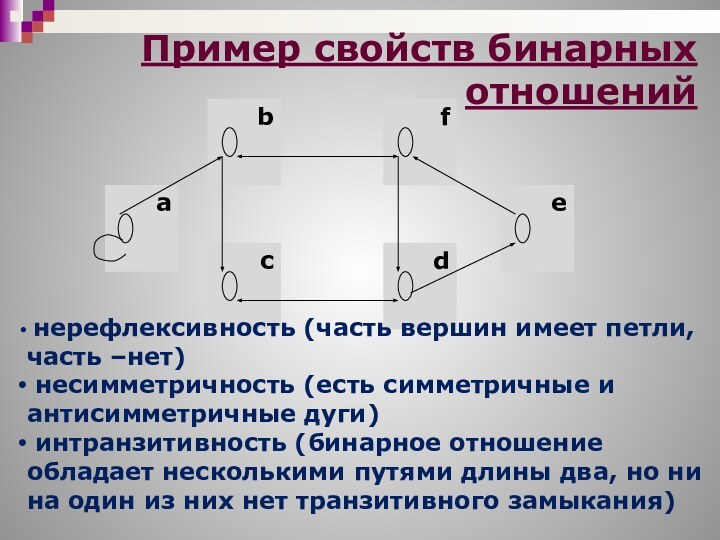
.
Фактор-множество
R/M =
Рефлексивность
Транзитивность