Презентация на тему Координаты вектора в пространстве

нем рассмотрена темы 10-го класса- Векторы в пространстве, и

действия над векторами в пространстве.
Уверена вам понравится!!!

Цели работы

Далее

над векторами:
Тест
Об авторе
Содержание

1) . Направление вектора определяется указанием его начала и

конца. На чертеже направление вектора отмечается стрелкой. Для обозначения векторов будем пользоваться строчными латинскими буквами а, Ь, с, ... . Можно также обозначить вектор указанием его начала и конца. При этом начало вектора ставится на первом месте. Вместо слова «вектор» над буквенным обозначением вектора иногда ставится стрелка или черта. Вектор на рисунке 1 можно обозначить так:

или

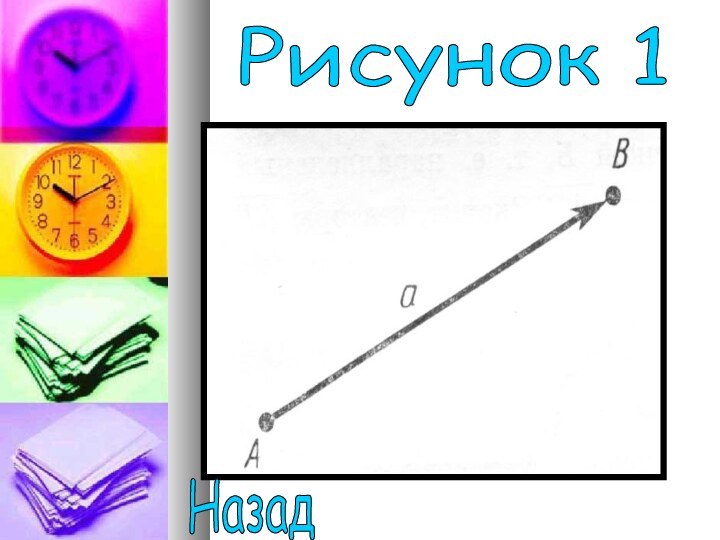
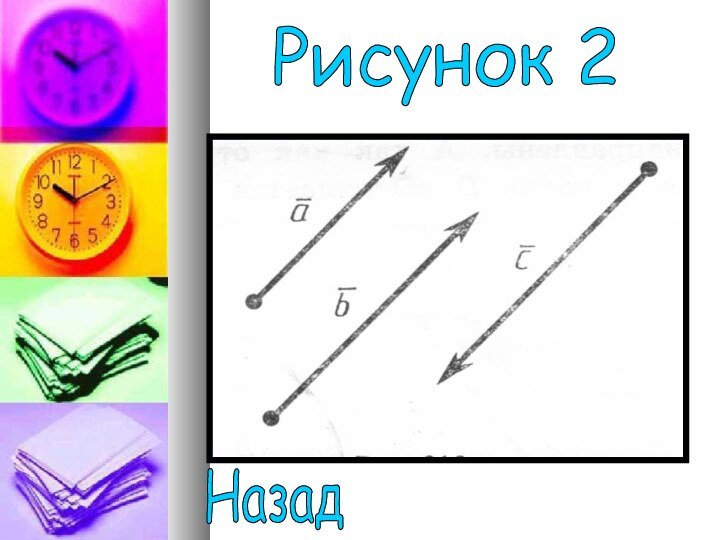
Величина и направление
вектора

Далее

Содержание

называются одинаково направленными, если полупрямые АВ и СD

одинаково направлены. Векторы называются противоположно направленными, если полупрямые АВ и СD противоположно направлены. На рисунке 212 векторы одинаково направлены, а векторы противоположно направлены.
Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютная величина
вектора а обозначается .
Начало вектора может совпадать с его концом. Такой вектор будем называть нулевым вектором. Нулевой вектор обозначается нулем с черточкой . О направлении нулевого вектора не говорят. Абсолютная величина нулевого вектора считается равной нулю(Рисунок 2) .

Величина и направление
вектора

Назад

называется направленный отрезок. Буквально так же, как и на

плоскости, определяются основные понятия для векторов в пространстве: абсолютная величина вектора, направление вектора, равенство векторов.
Координатами вектора с началом в точке
А1(х1; у1; z1) и концом в точке А2(х2;y2;z2) называются числа х2 - х1, у2 - у1, z2 - z1. Так же, как и на плоскости, доказывается, что равные векторы имеют соответственно равные координаты и, обратно, векторы с соответственно равными координатами равны. Это дает основание для обозначения вектора его координатами:
а (a1, a2; а3) или просто (а1; а2; а3).

Содержание

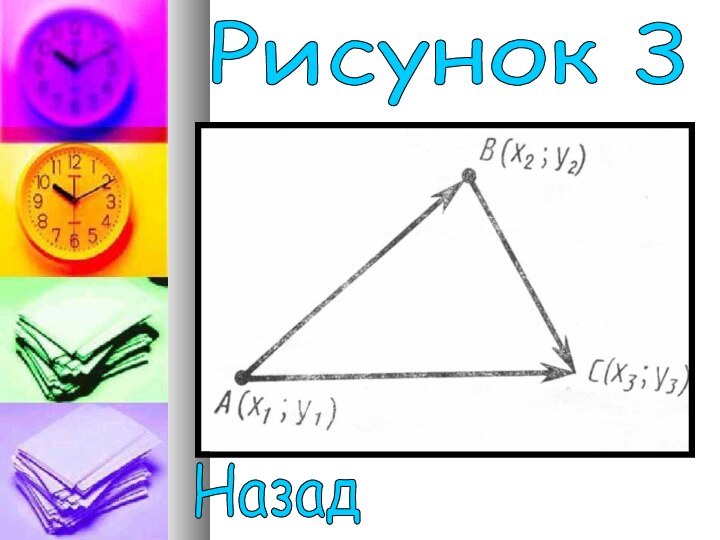
Векторы в пространстве

Задача 1

действия над векторами: сложение, разность , умножение на число

и скалярное произведение.

Действия над векторами
в пространстве

Содержание

и (b1; b2; b3) называется вектор:

(a1 + b1; а2 + b2; а3 + b3).
Так же,как и на плоскости, доказывается векторное равенство (доказательство) :

Сумма векторов

Назад

Задача 3

точки (рисунок 3) .Вектор имеет координаты х2-х1,y2-y1,

вектор имеет координаты х3 - х2, у3-y2. Следовательно, вектор имеет координаты х3-х1, у3-у1. А это есть координаты вектора . Значит, векторы равны. Теорема доказана.

Доказательство

Назад

называется такой вектор (с1; с2;c3), который в

сумме с вектором дает вектор : Ь . Отсюда находим координаты вектора :
c1=a1-b1;c2=a2-b2;c3=a3-b3

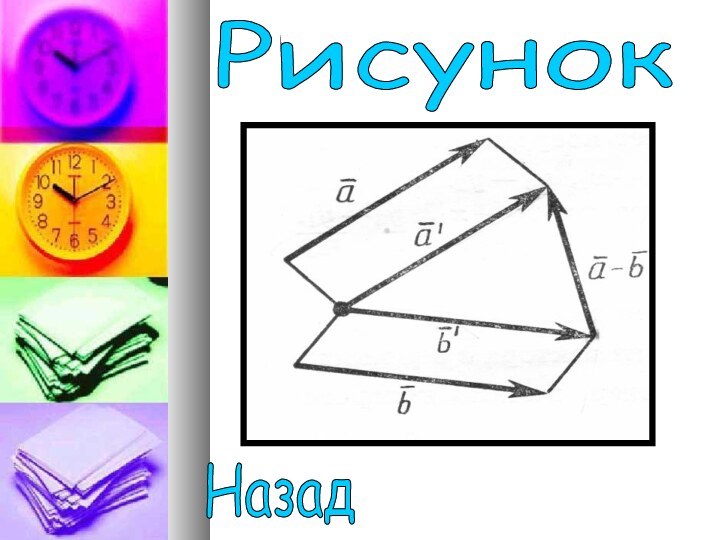
Разность векторов

Назад

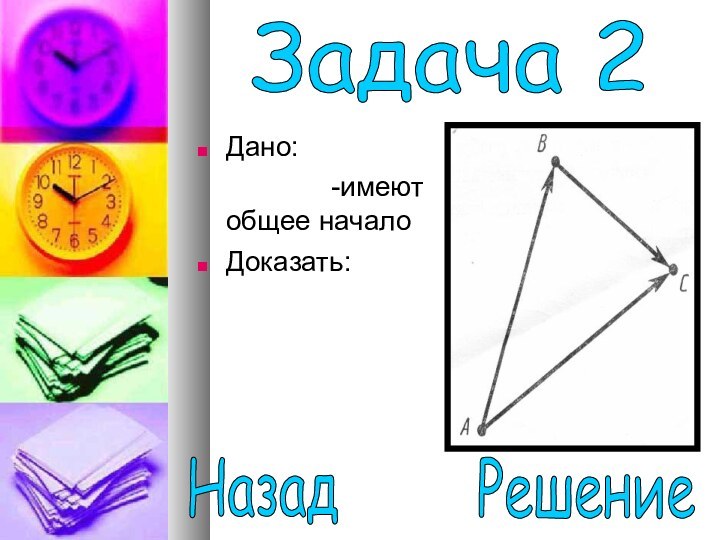
Задача 2

-имеют общее начало
Доказать:

Задача 2
Решение
Назад

D(-2;3;-1)
Найти:
Среди всех векторов указать равные
Надо найти

координаты всех векторов и сравнить эти координаты.
:1-2=-1, 0-7=- 7, 3-(-3)=6
У вектора такие же координаты: -3-(-2)=-1, -4-3=-7, 5-(-1)=6. Значит и равны. Другой парой равных векторов будут и

Задача 1

Назад

Решение:

вектор с началом в точке A(1;1;1) и концом B

на плоскости xy.

Координата z точки В равна нулю. Координаты вектора : х-1, у-1, 0-1 1=-1. Из коллинеарности векторов и получаем пропорцию:


Отсюда находим координаты x, y точки B:

Задача 3

Назад

Решение:

на число λ называется вектор

Так же, как

и на плоскости, доказывается, что абсолютная величина вектора λа равна \λ\ \ \, а направление совпадает с направлением вектора , если λ> 0, и противоположно направлению вектора , если λ<0.

Произведение вектора

Назад

и

называется число a1b1 +a2b2 +a3b3. Буквально так же, как и на плоскости, доказывается, что скалярное произведение векторов равно произведению их абсолютных величин на косинус угла между векторами.

Скалярное произведение
векторов

Назад

Задача 4

D(2;-3;1)
Найти:
cosφ=?
Решение:
Координатами вектора будут:

1-0=1, -1-1=-2, 2-(-1)=3


Координатами вектора будут:
2-3=-1, -3-1=-4, 1- 0=1

Значит,

Задача 4

Назад