Презентация на тему Көпжақтың қимасын салу, геометрия 10 сынып

әртүрлі жағында жатса, онда осы жазықтық көпжақтың қима жазықтығы

деп атайды

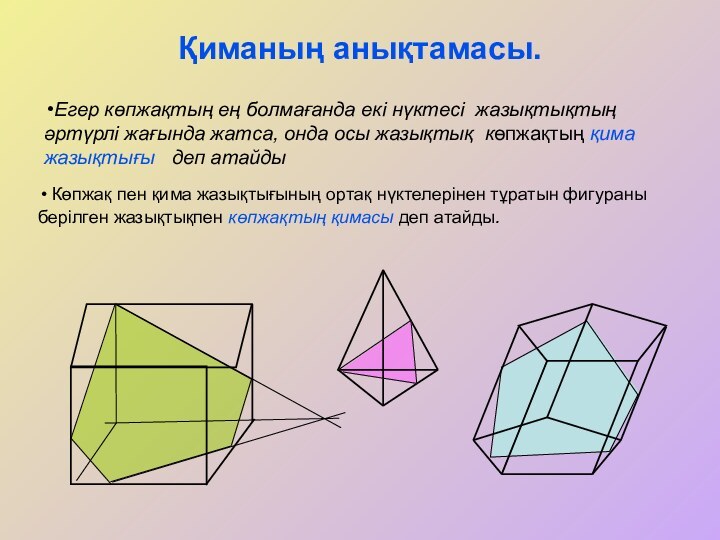
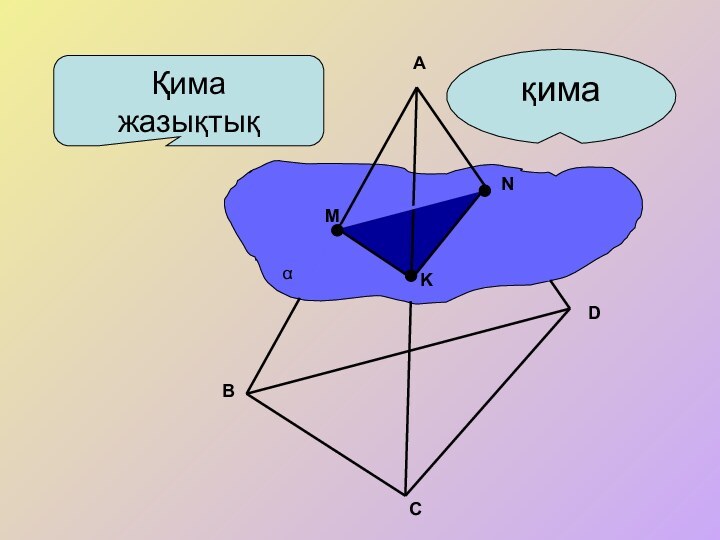
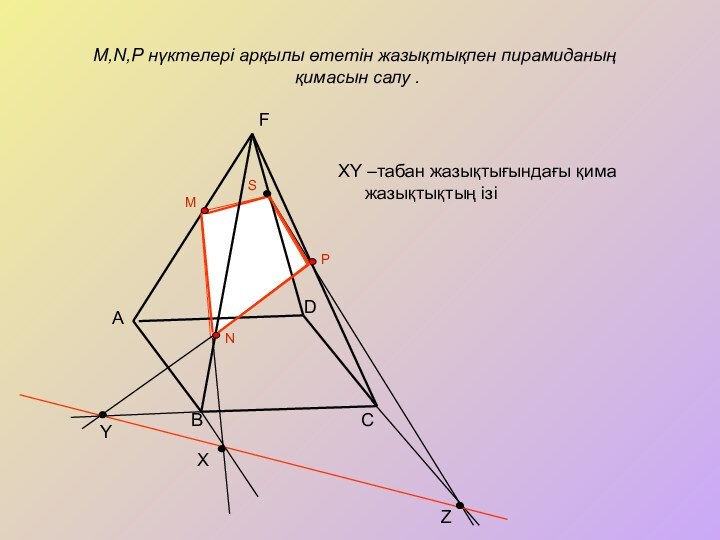
Көпжақ пен қима жазықтығының ортақ нүктелерінен тұратын фигураны берілген жазықтықпен көпжақтың қимасы деп атайды.

Салу:





А
В
С
D
P
M
N
2. PN кесіндісін



А
В
С
D
M
L
1. MP кесіндісін

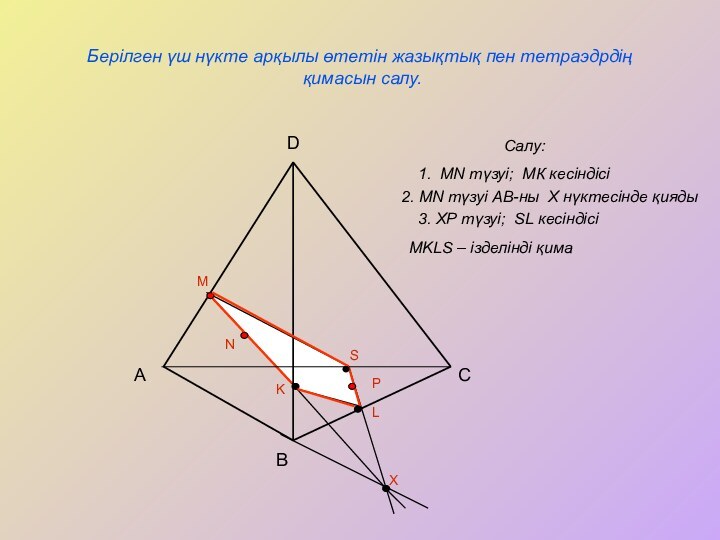
Салу:

3. MN кесіндісін

MPN – ізделінді қима

1. MN кесіндісі

2. NP сәулесі; NP сәулесі L нүктесінде АС-ны қияды

3. ML кесіндісі

MNL – ізделінді қима

салу.
Салу:


А
С
В
D
N
P
Q





R

E
1. NQ кесіндісін
2. NP кесіндісін
NP түзуі АС-ны

Е нүктесінде қияды

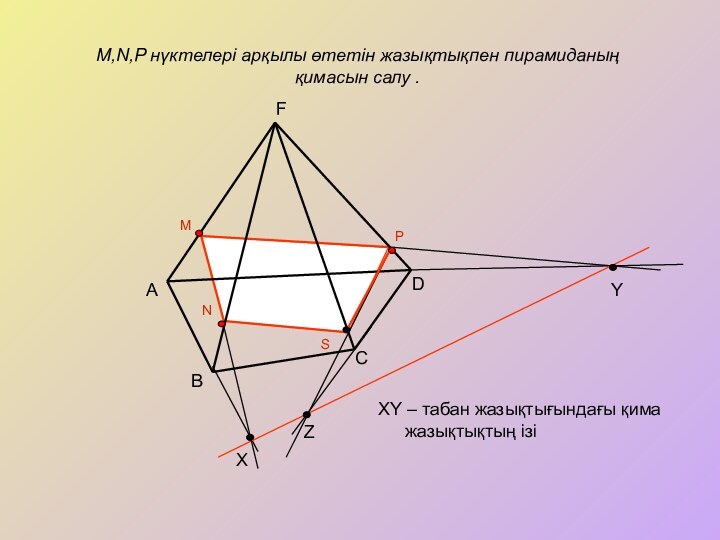
3. EQ түзуі

EQ түзуі BC-ны R нүктесінде қияды

NQRP – ізделінді қима

қимасын салу.
Салу:
А
B
C
D
M
N
P
X
K
S
L



1. MN түзуі; МК кесіндісі

2. MN түзуі АВ-ны

Х нүктесінде қияды

3. ХР түзуі; SL кесіндісі

MKLS – ізделінді қима

метода заключается в построении вспомогательной прямой, являющейся изображением линии

пересечения секущей плоскости с плоскостью какой-либо грани фигуры . Удобнее всего строить изображение линии пересечения секущей плоскости с плоскостью нижнего основания. Эту линию называют следом секущей плоскости. Используя след, легко построить изображения точек секущей плоскости, находящихся на боковых ребрах или гранях фигуры .    

салу .
XY – табан жазықтығындағы қима жазықтықтың ізі

D

C

B

А

Z

Y

X

M

N

P

S

F

арқылы өтетін жазықтықпен пирамиданың қимасын салу .
А
F

салу.
M
A
1)
1)
2)
2)
В
С
К
В
A
С






E
F
H
E
H
F

1 -нұсқа
2 -нұсқа



D
C
B
M
N
P
А
F



D
C
B
M
N
P
А
F