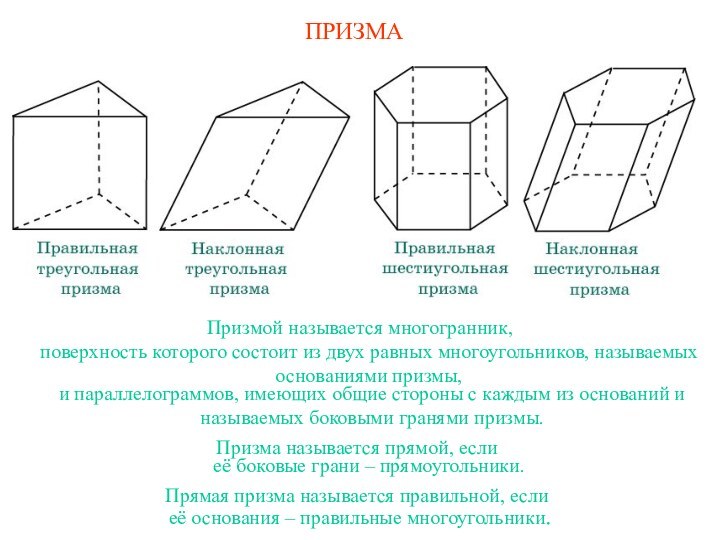
многоугольников, называемых основаниями призмы,
и параллелограммов, имеющих общие стороны с
каждым из оснований и называемых боковыми гранями призмы.Призма называется прямой, если
её боковые грани – прямоугольники.
Прямая призма называется правильной, если
её основания – правильные многоугольники.