- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Поговорим о многогранниках
Содержание
- 2. Ни одни геометрические тела не
- 4. Правильные многогранники Еще в древней Греции были известны пять удивительных многогранников.
- 5. Их изучали ученые, ювелиры, священники, архитекторы. Этим
- 7. Правильные многогранники
- 8. Тетраэдр Тетраэдр (tetra – четыре,
- 9. Гексаэдр Гексаэдр (куб, hexa –
- 10. Октаэдр Октаэдр (okto – восемь).
- 11. Додекаэдр Существует правильный многогранник, у
- 12. Икосаэдр Существует правильный многогранник, у
- 13. Полуправильные многогранники
- 14. Определение: Полуправильным называется выпуклый многогранник,
- 15. Тела Архимеда
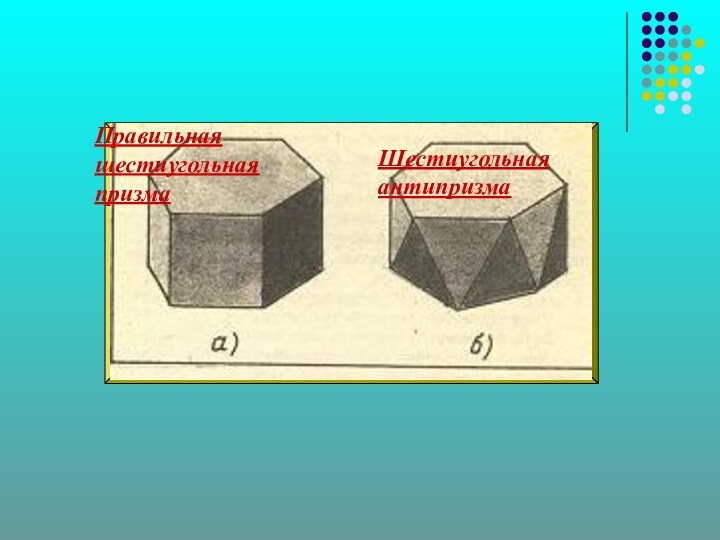
- 16. Правильная шестиугольная призмаШестиугольная антипризма
- 17. Усеченный тетраэдрУсеченный икосаэдрИкосододекаэдрУсеченный икосододекаэдр
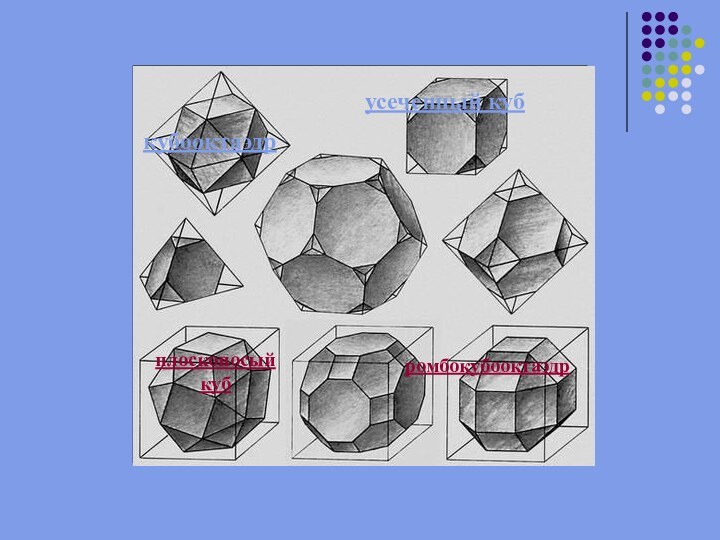
- 18. кубооктаэдрусеченный кубплосконосый кубромбокубооктаэдр
- 19. Кубооктаэдр Этот полуправильный многогранник получается, если
- 20. Усеченный куб Если указанным способом срезать
- 21. ромбоикосододекаэдрплосконосый додекаэдр
- 22. Звездчатые многогранники
- 23. Тела Кеплера- Пуансо Кроме правильных и
- 24. Малый звездчатый додекаэдрБольшой звездчатый додекаэдр
- 25. Примечание: Из тетраэдра, куба и октаэдра
- 26. Это интересноЗвездчатые многогранники очень декоративны, что позволяет
- 27. Скачать презентацию
- 28. Похожие презентации
Ни одни геометрические тела не обладают таким совершенством и красотой , как правильные многогранники. "Правильных многогранников вызывающе мало, -написал когда-то Л.Кэролл, - но этот весьма скромный по численности отряд сумел пробраться в самые глубины

























Слайд 4
Правильные многогранники
Еще в древней Греции
были известны пять
удивительных многогранников.
Слайд 5 Их изучали ученые, ювелиры, священники, архитекторы. Этим многогранникам
даже приписывали магические свойства. Древнегреческий ученый и философ Платон
(IV–V в до н. э.) считал, что эти тела олицетворяют сущность природы. В своем диалоге «Тимей» Платон говорит, что атом огня имеет вид тетраэдра, земли – гексаэдра (куба), воздуха – октаэдра, воды – икосаэдра. В этом соответствии не нашлось места только додекаэдру и Платон предположил существование еще одной, пятой сущности – эфира, атомы которого как раз и имеют форму додекаэдра. Ученики Платона продолжили его дело в изучении перечисленных тел. Поэтому эти многогранники называют платоновыми телами
Слайд 8
Тетраэдр
Тетраэдр (tetra – четыре,
hedra – грань). Правильный тетраэдр – правильный четырехгранник, то
есть тетраэдр с равными ребрами, представляет собой правильный многогранник, все грани которого – правильные треугольники и из каждой вершины которого выходит ровно три ребра.Очевидно, что тетраэдр с заданной длиной ребра единственен. Все остальные тетраэдры подобны ему и определяются длиной ребра/
Слайд 9
Гексаэдр
Гексаэдр (куб, hexa –
шесть). Гексаэдр – правильный многогранник, все грани которого –
квадраты, и из каждой вершины выходит три ребра.
Слайд 10
Октаэдр
Октаэдр (okto – восемь).
Это
правильный многогранник,
все грани которого – правильные треугольники
и к каждой вершине прилегают четыре грани
Слайд 11
Додекаэдр
Существует правильный многогранник, у которого
все грани правильные пятиугольники и из каждой вершины выходит
3 ребра. Этот многогранник имеет 12 граней, 30 ребер и 20 вершин и называется додекаэдром (dodeka – двенадцать).
Слайд 12
Икосаэдр
Существует правильный многогранник, у которого
все грани – правильные треугольники, и из каждой вершины
выходит 5 ребер. Этот многогранник имеет 20 граней, 30 ребер, 12 вершин и называется икосаэдром (icosi – двадцать).
Слайд 14
Определение:
Полуправильным называется выпуклый многогранник, гранями
которого являются правильные многоугольники (возможно с разным числом сторон),
причем в каждой вершине сходится одинаковое число граней.
Слайд 19
Кубооктаэдр
Этот полуправильный многогранник получается, если провести
в кубе отсекающие плоскости через середины ребер, выходящих из
одной вершины.Его гранями являются шесть квадратов, как у куба, и восемь правильных треугольников, как у октаэдра. Отсюда и его название.
Слайд 20
Усеченный куб
Если указанным способом срезать вершины
куба, то получится полуправильный многогранник, который и называется усеченным
кубом
Слайд 23
Тела Кеплера- Пуансо
Кроме правильных и полуправильных
многогранников красивые формы имеют так называемые звездчатые многогранники.
Правильных звездчатых многогранников всего четыре. Первые два открыты И. Кеплером, а два других почти 200 лет спустя построил Л. Пуансо.
Слайд 25
Примечание:
Из тетраэдра, куба и октаэдра звездчатые
многогранники не получаются. Из додекаэдра получается три. Икосаэдр имеет
одну звездчатую форму – большой икосаэдр.
Слайд 26
Это интересно
Звездчатые многогранники очень декоративны, что позволяет широко
применять их при изготовлении всевозможных украшений. Применяются они и
в архитектуре.Многие формы звездчатых многогранников подсказывает сама природа. Снежинки – это звездчатые многогранники.