Презентация на тему Квадратичная функция (11 класс)

Содержание:

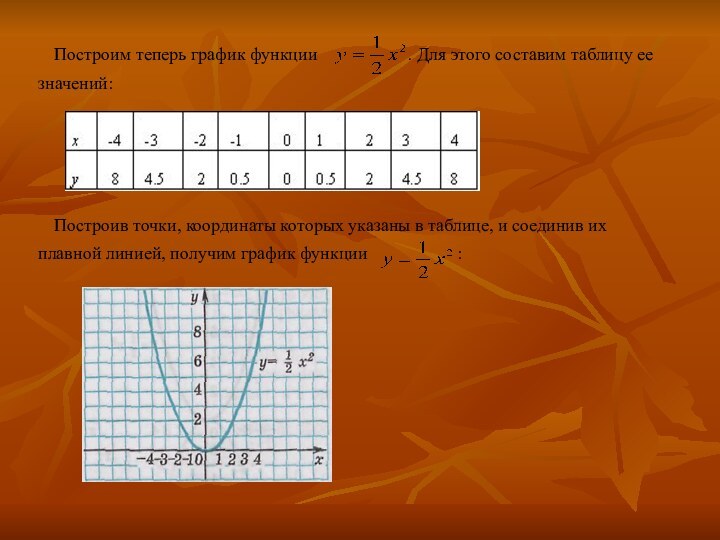
1. Функция

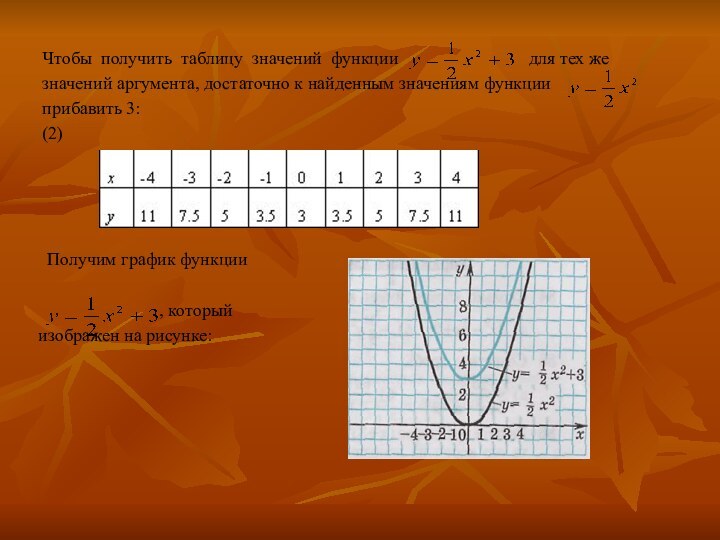
, её график и свойства
2. Графики функций и
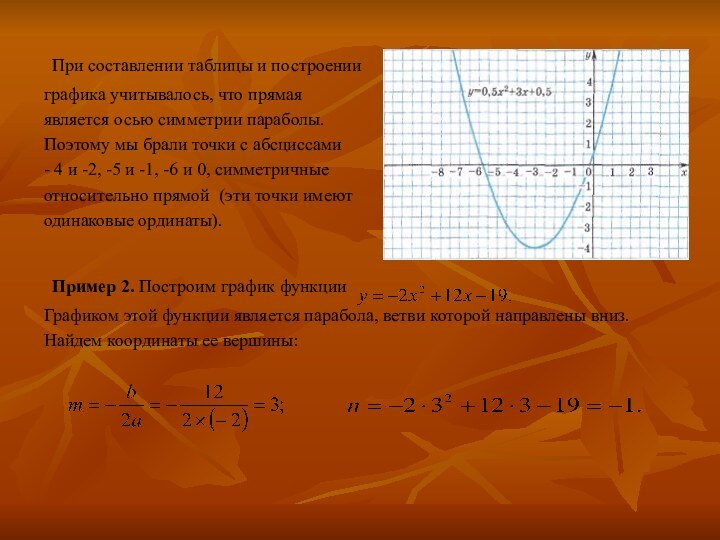
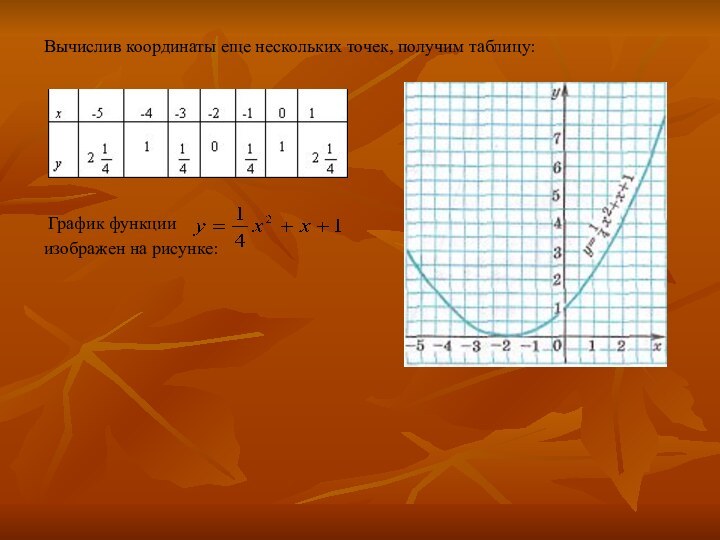
3. Построение графика квадратичной функции

ЕЕ ГРАФИК И СВОЙСТВА
Определение. Квадратичной функцией

называется функция, которую можно задать формулой вида , где x - независимая переменная, a, b и c - некоторые числа, причем .
Примером квадратичной функции является зависимость пути от времени при
равноускоренном движении. Если тело движется с ускорением а и к началу
отсчета времени t прошло путь м, имея в этот момент скорость м/с, то
зависимость пройденного пути s (в метрах) от времени t (в секундах) выражается
формулой:

Если, например, a= 6, то формула примет вид:

случая - функции

.
При а = 1 формула принимает вид . С этой функцией мы уже
встречались. Графиком этой функции является парабола.
Построим график функции . Составим таблицу значений этой функции:




Построим точки, координаты которых указаны в таблице. Соединив их плавной
линией, получим график функции .

значение функции

больше соответствующего
значения функции в 2 раза. Если переместить каждую точку графика
функции вверх так, чтобы расстояние от этой точки до оси х
увеличилось в 2 раза, то она перейдет в точку графика функции ,
при этом каждая точка этого графика может быть получена из некоторой
точки графика функции .
Иными словами, график функции можно получить из параболы
растяжением от оси х в 2 раза.

. Для этого

составим таблицу ее
значений:




Построив точки, координаты которых указаны в таблице, и соединив их
плавной линией, получим график функции :

значение функции

меньше соответствующего
значения функции в 2 раза. Если переместить каждую точку графика
функции вниз так, чтобы расстояние от этой точки до оси х
уменьшилось в 2 раза, то она перейдет в точку графика функции
причем каждая точка этого графика может быть получена из некоторой
точки графика функции .
Таким образом, график функции можно получить из параболы
сжатием к оси х в 2 раза.

можно получить из параболы

растяжением от оси х в а раз, если а>1, и сжатием к оси х в раз,
если 0< а<1.
Рассмотрим теперь функцию при а<0.

Построим график функции , для чего составим таблицу значений
этой функции:




Воспользовавшись этой таблицей,
построим график функции :

График функции

может быть

получен из графика функции

с помощью симметрии относительно оси х.

при

а>0.


1. Если x=0, то y=0. График функции проходит через начало координат.
2. Если , то y>0. График функции расположен в верхней
полуплоскости.
3. Противоположным значениям аргумента соответствуют равные
значения функции. График функции симметричен относительно оси у.
4. Функция убывает в промежутке и возрастает в промежутке
.
5. Наименьшее значение, равное нулю, функция принимает при x=0,
наибольшего значения функция не имеет. Областью значений функции
является промежуток .

Свойства функции при а<0.

1. Если x=0, то y=0. График функции проходит через начало координат.
2. Если , то y<0. График функции расположен в нижней полуплоскости.
3. Противоположным значениям аргумента соответствуют равные значения функции. График функции симметричен относительно оси у.
4. Функция возрастает в промежутке и убывает в промежутке
.
5. Наибольшее значение, равное нулю, функция принимает при x=0, наименьшего значения функция не имеет. Областью значений функции является промежуток .

И

График функции y=f (x)+n можно получить из графика функции y=f (x) с
помощью параллельного переноса вдоль оси у на п единиц вверх, если n>0,
или на - п единиц вниз, если n<0.
График функции y=f (x-m) можно получить из графика функции у =f (x) с
помощью параллельного переноса вдоль оси х на т единиц вправо, если
m>0, или на - т единиц влево, если m<0.
График функции y=f (x-m)+n можно получить из графика функции y=f (x)
с помощью двух соответствующих параллельных переносов.

график функции

.
С этой целью в одной системе координат построим графики функций
и .

Составим таблицу значений функции :
(1)





График функции изображен
на рисунке:

для тех же
значений аргумента, достаточно к найденным значениям функции
прибавить 3:
(2)




Получим график функции

, который
изображен на рисунке:

- парабола, полученная в результате сдвига

вверх графика функции .

Вообще график функции
является параболой, которую можно
получить из графика функции
с помощью параллельного переноса
вдоль оси у на п единиц вверх, если n>0,
или на - п единиц вниз, если n<0.

и выясним,
что представляет собой ее график.
Для этого в одной системе координат построим графики функций
и .
Для построения графика функции воспользуемся таблицей
(1). Составим теперь таблицу значений функции .
При этом в качестве значений аргумента выбе­рем те, которые на 5
больше соответствующих значений аргумента в таблице (1). Тогда
соответствующие им значения функции будут те же,
которые записаны во второй строке таблицы (1):
(3)

- парабола,
полученная в результате сдвига вправо графика
функции .
Вообще график функции
является параболой, которую можно получить
из графика функции с помощью
параллельного переноса вдоль оси х на т единиц
вправо, если m>0, или на - т единиц влево,
если m<0.

Полученные выводы позволяют понять, что представляет собой график
Функции .
Рассмотрим, например, функцию Ее график можно

получить из графика функции с помощью двух параллельных
переносов - сдвига параболы на 3 единицы вправо и на 2 единицы вверх.

является

параболой, которую можно получить
из графика функции с помощью двух
параллельных переносов: сдвига вдоль оси х на
т единиц вправо, если m>0, или на - т единиц
влево, если m<0 , и сдвига вдоль оси у на n
единиц вверх - если n>0, или на - п единиц вниз,
если n<0.
Заметим, что производить параллельные переносы можно
в любом порядке: сначала выполнить параллельный перенос
вдоль оси x, а затем вдоль оси у или наоборот.

ФУНКЦИИ

Рассмотрим квадратичную функцию

. Выделим из трехчлена
квадрат двучлена:






Отсюда Мы получили формулу вида ,

где
Значит, график функции есть парабола, которую можно
получить из графика функции с помощью двух параллельных
переносов – сдвига вдоль оси х и сдвига вдоль оси у.

есть парабола,
вершиной которой является точка (m;n), где
Осью симметрии параболы служит прямая x=m параллельная оси у.
При a>0 ветви параболы направлены вверх, при a<0 - вниз.

Чтобы построить график квадратичной функции, нужно:

1) найти координаты вершины параболы и отметить ее в
координатной плоскости;
2) построить еще несколько точек, принадлежащих параболе;
3) соединить отмеченные точки плавной линией.

является парабола, ветви которой
направлены вверх. Найдем координаты m и n вершины этой параболы:




Значит, вершиной параболы является точка (-3; -4).
Составим таблицу значений функции:





Построив точки, координаты которых указаны в таблице, и соединив их плавной
линией, получим график функции .

прямая
является осью симметрии параболы.
Поэтому мы брали точки

с абсциссами
- 4 и -2, -5 и -1, -6 и 0, симметричные
относительно прямой (эти точки имеют
одинаковые ординаты).

Пример 2. Построим график функции
Графиком этой функции является парабола, ветви которой направлены вниз.
Найдем координаты ее вершины:

линией точки,
координаты которых указаны в таблице,
получим график

функции :

Пример 3. Построим график функции .
Графиком функции является парабола, ветви которой
направлены вверх. Найдем координаты ее вершины: