Презентация на тему Квадратичная функция.

Содержание

2. Квадратичная функция:Квадратичной функцией называется функция, которую можно
3. Парабола:Парабола - от греческого «пара» - рядом
4. Свойства параболы:Парабола симметрична относительно прямой проходящей через
5. Свойства функции у = х21.Если х=0, то
6. Скачать презентацию
7. Похожие презентации

Квадратичная функция:Квадратичной функцией называется функция, которую можно записать формулой вида y=ax2+bx+c, где x – независимая переменная, a, b и c – некоторые числа, причем a≠0. Графиком квадратичной функции является парабола.

Парабола:Парабола - от греческого «пара» - рядом и «баллейн» - бросать. Параболой

Свойства параболы:Парабола симметрична относительно прямой проходящей через её вершину и направленной вдоль

Свойства функции у = х21.Если х=0, то у=0, т.е. парабола имеет с

Слайды презентации

Слайд 2 Квадратичная функция:

Квадратичной функцией называется функция, которую можно записать

Квадратичная функция:Квадратичной функцией называется функция, которую можно записать формулой вида y=ax2+bx+c,

формулой вида y=ax2+bx+c, где x – независимая переменная, a,

b и c – некоторые числа, причем a≠0. Графиком квадратичной функции является парабола.

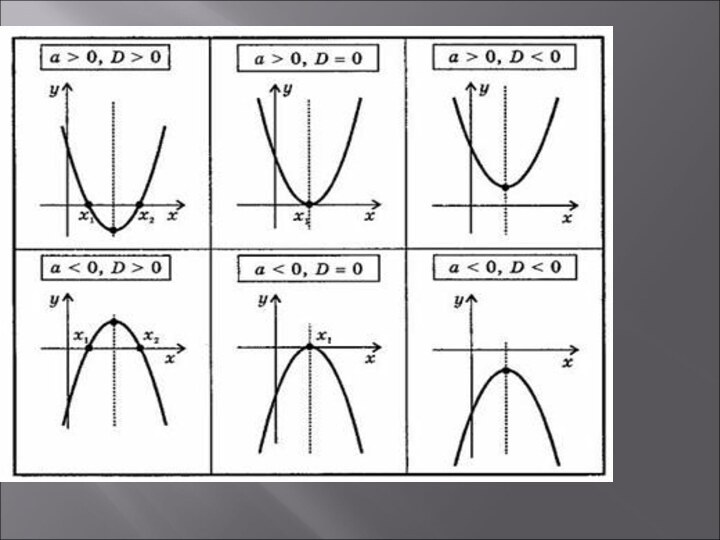
Слайд 3 Парабола:

Парабола - от греческого «пара» - рядом и

Парабола:Парабола - от греческого «пара» - рядом и «баллейн» - бросать.

«баллейн» - бросать.
Параболой называется кривая, точки которой одинаково

удалены от некоторой точки, называемой фокусом, и от некоторой прямой, называемой директрисой параболы.

Слайд 4 Свойства параболы:

Парабола симметрична относительно прямой проходящей через её

Свойства параболы:Парабола симметрична относительно прямой проходящей через её вершину и направленной

вершину и направленной вдоль ветвей параболы.
Ось симметрии пересекает

параболу только в её вершине.
Парабола имеет только одну вершину.
Парабола бесконечна.

Слайд 5 Свойства функции у = х2
1.Если х=0, то у=0,

Свойства функции у = х21.Если х=0, то у=0, т.е. парабола имеет

т.е. парабола имеет с осями координат общую точку (0;

0)-начало координат.
2. Если х≠0, то у>0, т.е. все точки параболы, кроме начала координат, лежат над осью абсцисс.
3.Множеством значений функции - промежуток [0; +∞).
4. парабола симметрична относительно оси ординат (функция четная).
5.На промежутке [0; + ∞) функция возрастает.
6.На промежутке (-∞; 0] функция убывает.
7.Наименьшее значение функции равно 0. Наибольшего значения не существует.