,
отличное от 1,и уравнения ,
сводящиеся к этому
виду , называются показательными.
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Решение показательных уравнений
Содержание
- 2. 11234
- 3. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯУравнения вида af(x)=ag(x),где a -
- 4. 1. Решаемые переходом к одному основанию.2. Решаемые
- 5. 54x+2 = 12554x+2 =534x+2 = 34 x
- 6. Решение путем деления Если обе части уравнения
- 7. 3х=2х разделим обе части на 2х3х: 2х=2х: 2х(1,5)х=1(1,5)х=(1,5)0 х =0Пример показательного уравнения,которое решается путем деления
- 8. Решение разложением на множителиЕсли одна из частей
- 9. Пример показательного уравнения, одна из частей которого содержит алгебраическую сумму3х+1-2*3х-2=253х-2*(3х+1-(х-2)-2)=253х-2*(33-2)=253х-2*25=253х-2=13х-2=30х-2=0х=2
- 10. Сведение показательных уравнений к квадратным
- 11. Найдите корень уравнения устно:
- 12. Найдите корень уравнения устно:
- 13. Скачать презентацию
- 14. Похожие презентации
11234
Слайд 3
ПОКАЗАТЕЛЬНЫЕ
УРАВНЕНИЯ
Уравнения вида af(x)=ag(x),где
a - положительное число
,
виду ,называются показательными.
Слайд 4
1. Решаемые переходом к одному основанию.
2. Решаемые переходом
к одному показателю степени.
3. Решаемые вынесением общего множителя за
скобку.4. Сводимые к квадратным или кубическим введением замены переменной.
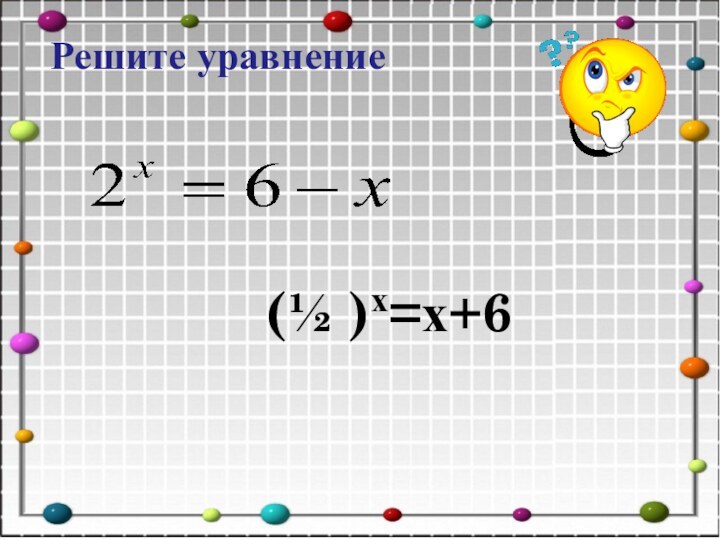
ОСНОВНЫЕ ВИДЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ
Слайд 5
54x+2 = 125
54x+2 =53
4x+2 = 3
4 x =
1
x = 0,25
Ответ: x =0,25
РЕШЕНИЕ УРАВНЕНИЙ СВЕДЕНИЕМ ОБЕИХ ЧАСТЕЙ
УРАВНЕНИЯ К ОДНОМУ ОСНОВАНИЮ
Слайд 6
Решение путем деления
Если обе части уравнения степени
с равными показателями ,
то уравнение решают делением
обеих
частей на любую из степеней.
Слайд 7
3х=2х разделим обе части на 2х
3х: 2х=2х: 2х
(1,5)х=1
(1,5)х=(1,5)0
х =0
Пример показательного уравнения,
которое решается путем деления
Слайд 8
Решение разложением на множители
Если одна из частей уравнения
содержит алгебраическую сумму с одинаковыми основаниями , показатели которых
отличаются на постоянное слагаемое , то такое уравнение решается разложением на множители.Слайд 9 Пример показательного уравнения, одна из частей которого содержит
алгебраическую сумму
3х+1-2*3х-2=25
3х-2*(3х+1-(х-2)-2)=25
3х-2*(33-2)=25
3х-2*25=25
3х-2=1
3х-2=30
х-2=0
х=2
Слайд 10
Сведение показательных уравнений к квадратным
Одним
из наиболее распространенных методов решения уравнений (в том числе
и показательных) является метод замены переменной, позволяющий свести то или иное уравнение к алгебраическому (как правило, квадратному) уравнению.x
