Слайд 2
Содержание
Введение
Призма в древности
Призма в геометрии
Теоремы
Задачи
Используемые источники
Слайд 3
Введение
Рассмотрим два равных многоугольника A1A2…An и B1B2…Bn
, расположенных в параллельных плоскостях α и β так,
что отрезки A1B1 ,A2B2, …,AnBn, соединяющие соответственные вершины многоугольников, параллельны. Каждый из n четырехугольников A1A2B2B1, A2A3B3B2, …, AnA1B1Bn (1) является параллелограммом, так как имеет попарно параллельные противоположные стороны. Например в четырехугольнике A1A2B2B1 стороны A1B1 и A2B и параллельны по условию, а стороны A1A2 и B1B2 – по свойству параллельных плоскостей, пересеченных третьей плоскостью.
Многогранник, составленный из двух равных многоугольников A1A2…An и B1B2…Bn , расположенных в параллельных плоскостях, и n параллелограммов (1), называется призмой.
Слайд 4
Введение
A
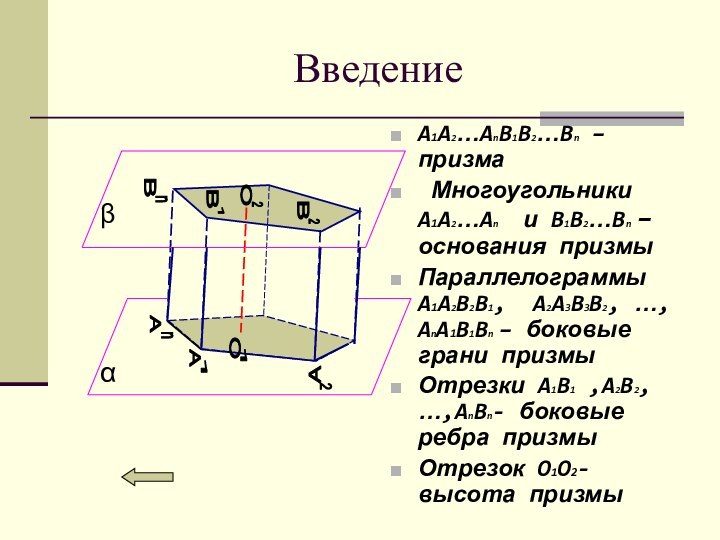
A1A2…AnB1B2…Bn – призма
Многоугольники A1A2…An и B1B2…Bn
– основания призмы
Параллелограммы A1A2B2B1, A2A3B3B2, …, AnA1B1Bn – боковые
грани призмы
Отрезки A1B1 ,A2B2, …,AnBn- боковые ребра призмы
Отрезок O1O2- высота призмы
A
1
2
A
n
2
1
n
B
B
B
O
O
1
2
α
β
Слайд 5
Призма в древности
Подобно тому, как треугольник в понимании
Евклида не являются пустым, т. е. представляет собой часть
плоскости, ограниченную тремя неконкурентными (т. е. не пересекающимися в одной точке) отрезками, так и многогранник у него не пустой, не полый, а чем-то заполненный (по-нашему - частью пространства). В античной математике, однако, понятия отвлеченного пространства еще не было. Евклид определяет призму как телесную фигуру, заключенную между двумя равными и параллельными плоскостями (основаниями) и с боковыми гранями - параллелограммами. Для того чтобы это определение было вполне корректным, следовало бы, однако, доказать, что плоскости, проходящие через пары непараллельных сторон оснований, пересекаются по параллельным прямым.
Слайд 6
Призма в древности
Евклид употребляет термин “плоскость” как в
широком смысле (рассматривая ее неограниченно продолженной во все направления),
так и в смысле конечной, ограниченной ее части, в частности грани, аналогично применению им термина “прямая” (в широком смысле - бесконечная прямая и в узком - отрезок). В XVIII в. Тейлор дал такое определение призмы: это многогранник, у которого все грани, кроме двух, параллельны одной прямой.
В памятниках вавилонской и древнеегипетской архитектуры встречаются такие геометрические фигуры, как куб, параллелепипед, призма. Важнейшей задачей египетской и вавилонской геометрии было определение объема различных пространственных фигур. Эта задача отвечала необходимости строить дома, дворцы, храмы и другие сооружения.
Слайд 7
Призма в древности
Часть геометрии, в которой изучаются свойства
куба, призмы, параллелепипеда и других геометрических тел и пространственных
фигур, издавна называется стереометрией; Слово это греческого происхождения (“стереос” - пространственный, “метрео” - измеряю) и встречается еще у знаменитого древнегреческого философа Аристотеля. Стереометрия возникла позже, чем планиметрия. Евклид дает следующее определение призмы: “Призма есть телесная (т.е. пространственная) фигура, заключенная между плоскостями, из которых две противоположные равны и параллельны, остальные же - параллелограммы”. Тут, как и во многих других местах, Евклид употребляет термин “плоскость” не в смысле безгранично продолженной плоскости, а в смысле ограниченной ее части, грани, подобно тому как “прямая” означает у него и отрезок прямой.
Слайд 8
Призма в древности
Термин “призма” греческого происхождения и буквально
означает “отпиленное” (тело).
Термин “параллелепипедальное тело” встречается впервые у Евклида
и означает дословно “параллеле-плоскостное тело”. Греческое слово “кубос” употребляется Евклидом в том же смысле, что и наше слово “куб”.
Теоремы Евклида относятся только к сравнению объемов, так как непосредственное вычисление объемов тел. Евклид, вероятно, считал делом практических руководств по геометрии. В произведениях прикладного характера Герона Александрийского имеются правила для вычислений объема куба, призмы, параллелепипеда и других пространственных фигур.
Объемы зерновых амбаров и других сооружений в виде кубов, призм и цилиндров египтяне и вавилоняне, китайцы и индийцы вычисляли путем умножения площади основания на высоту.
Слайд 9
Призма в древности
Однако древнему Востоку были известны в
основном только отдельные правила, найденные опытным путем, которыми пользовались
для нахождения объемов для площадей фигур. В более позднее время, когда геометрия сформировалась как наука, был найден общий подход к вычислению объемов многогранников.
Среди замечательных греческих ученых V - IV вв. до н.э., которые разрабатывали теорию объемов, были Демокрит из Абдеры и Евдокс Книдский.
Евклид не применяет термина “объем”. Для него термин “куб”, например, означает и объем куба. В ХI книге “Начал” изложены среди других и теоремы следующего содержания.
1. Параллелепипеды с одинаковыми высотами и равновеликими основаниями равновелики.
2. Отношение объемов двух параллелепипедов с равными высотами равно отношению площадей их оснований.
3. В равновеликих параллелепипедах площади оснований обратно пропорциональны высотам.
Слайд 10
Призма в геометрии
Призма — многогранник, который состоит из двух
плоских равных многоугольников с соответственно параллельными сторонами и отрезков,
соединяющих соответствующие точки этих многоугольников.
Многоугольники называются основаниями призмы, а отрезки, соединяющие соответствующие вершины, — боковыми рёбрами призмы. Все боковые грани призмы – параллелограммы.
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой.
Слайд 11
Призма в геометрии
A
A1A2…AnB1B2…Bn – призма
Многоугольники A1A2…An
и B1B2…Bn – основания призмы
Параллелограммы A1A2B2B1, A2A3B3B2, …, AnA1B1Bn
– боковые грани призмы
Отрезки A1B1 ,A2B2, AnBn- боковые ребра призмы
Отрезок O1O2- высота призмы
A
1
2
A
n
2
1
n
B
B
B
O
O
1
2
Слайд 12
Призма в геометрии
Прямая призма — призма, у которой
боковое ребро перпендикулярно основанию.
ABCDEFKLMNOP- прямая правильная
призма
A
B
C
D
K
L
M
N
E
O
F
P
Слайд 13
Призма в геометрии
Прямая призма, основанием которой служит правильный
многоугольник, называется правильной призмой.
Боковое ребро прямой призмы, в том
числе и правильной, есть ее высота. Отрезок, концы которого - две вершины, не принадлежащие одной грани призмы, называют ее диагональю. Сечение призмы с плоскостью, проходящей через два боковых ребра, не лежащих в одной грани, называют диагональным сечением призмы.
Слайд 14
Призма в геометрии
Наклонная призма- призма, у которой боковое
ребро не перпендикулярно основанию.
ABCDEKLMNO- наклонная призма
KF- высота
Перпендикулярное сечение
A
B
C
D
K
L
M
N
E
O
F
Слайд 15
Призма в геометрии
Призма, основание которой - параллелограмм,
называется параллелепипедом.
В соответствии с определением параллелепипед
- это четырехугольная призма, все грани которой – параллелограммы. Параллелепипеды, как и призмы, могут быть прямыми и наклонными.
ABCDKLMN- параллелепипед
A
B
C
D
K
L
M
N
Слайд 16
Призма в геометрии
Прямой параллелепипед, основанием которого служит
прямоугольник, называют прямоугольным параллелепипедом. У прямоугольного параллелепипеда все грани
- прямоугольники.
Длины трех ребер прямоугольного параллелепипеда, имеющих общий конец, называют его измерениями. Куб - прямоугольный параллелепипед с равными измерениями. Все шесть граней куба - равные квадраты.
ABCDKLMN- куб
A
B
C
D
K
L
M
N
Слайд 17
Призма в геометрии
Призма:
Sбок=P l
Sполн=2Sо+Sбок
V=Sоl
Прямая призма: Sбок=Pоl(l=h)
Параллелепипед:
Sполн=2(ab+bc+ac)
V=abc
d²=a²+b²+c²
Куб:
Sполн=6a²
V=a³
d²=3a²
Обозначения:
V- объем;
Sполн-
площадь полной поверхности;
Sбок- площадь боковой поверхности;
Sо- площадь основания;
Pо- периметр
основания;
P - периметр перпендикулярного сечения;
l- длина ребра;
h- высота.
Слайд 18
Призма в геометрии
Призма называется описанной около цилиндра,
если ее основания описаны около основания цилиндра.
A1A2A3A4A5A6B1B2B3B4B5B6- призма описанная около цилиндра
A
B
A
A
A
A
A
B
B
B
B
B
3
1
2
2
3
4
4
1
5
5
6
6
h
r
Слайд 19
Призма в геометрии
Призма называется вписанной в цилиндр,
если ее основания вписаны в основания цилиндра.
A1A2A3A4A5A6B1B2B3B4B5B6- призма вписанная
в цилиндр
A
B
A
A
A
A
A
B
B
B
B
B
3
1
2
2
3
4
4
1
5
5
6
6
h
r
Слайд 20
Теоремы
Объем прямой призмы;
Объем наклонной призмы;
Площадь боковой поверхности призмы;
Площадь
боковой поверхности прямой призмы;
Слайд 21
Теоремы
Объем прямой призмы равен произведению площади основания
на высоту.
Доказательство
Сначала докажем теорему для треугольников прямой
призмы, а затем для произвольной призмы.
Рассмотрим прямую треугольную призму ABCA1B1C1 с объемом V и высотой h. Проведем такую высоту треугольника ABC(отрезок BD), которая разделяет этот треугольник на два треугольника (по крайней мере, одна высота треугольника этому условию удовлетворяет). Плоскость DD1D разделяет данную призму на две призмы,
Слайд 22
Теоремы
основаниями которых являются прямоугольные треугольники ABD
и BDC. Поэтому объемы V1 и V2 этих призм
соответственно равны SABD•h и SBDC•h. По свойству 2 объемов V=V1+V2, то есть V=SABD•h+SBDC•h=(SABD+SBDC)•h.
Таким образом, V=SABC•h (1)
A
1
A
B
B
1
1
1
C
C
D
D
Слайд 23
Теоремы
Докажем теорему для произвольной прямой призмы с высотой
h и площадью основания S. Такую призму можно разбить
на прямые треугольные призмы с высотой h. Например, на рисунке изображена пятиугольная призма, которая разбита на три прямые треугольные призмы. Выразим объем каждой треугольной призмы по формуле (1) и сложим эти объемы. Вынося за скобки общий множитель h, получим в скобках сумму площадей основания треугольных призм, то есть площадь S основания исходной призмы. Таким образом, объем исходной призмы равен произведению S•h. Теорема доказана.
Слайд 25
Теоремы
Объем наклонной призмы равен произведению площади основания на
высоту.
Доказательство
Сначала докажем теорему для треугольной призмы,
а затем- для произвольной призмы.
Рассмотрим треугольную призму с объемом V, площадью основания S и высотой h. Отметим точку О на одном из оснований призмы и направим ось Оx перпендикулярно к основаниям. Рассмотрим сечение призмы плоскостью, перпендикулярной к оси Оx и, значит, параллельной плоскости основания. Обозначим буквой x абсциссу точки пересечения этой плоскости с осью Оx, а через S(x)- площадь получившегося сечения.
Слайд 27
Теоремы
Докажем, что площадь S(x) равна площади S
основания призмы. Для этого заметим, что треугольники ABC(основания призмы)
и A1B1C1 (сечение призмы рассматриваемой плоскостью) равны. В самом деле, четырехугольник AA1B1B– параллелограмм (отрезки AA1 и B1B равны и параллельны), поэтому A1B1=AB . Аналогично доказывается, что B1C1=BC и A1C1=AC. Итак треугольники A1B1C1 и ABC равны по трем сторонам. Следовательно, S(x)=S. Применяя теперь основную формулу для вычисления объемов тел при a=0 и b=h, получаем
V=∫S(x)dx=∫Sdx=S∫dx=Sx|=Sh
Слайд 28
Теоремы
Докажем теорему для произвольной прямой призмы с высотой
h и площадью основания S. Такую призму можно разбить
на прямые треугольные призмы с высотой h. Выразим объем каждой треугольной призмы по доказанной нами формуле и сложим эти объемы. Вынося за скобки общий множитель h, получим в скобках сумму площадей основания треугольных призм, то есть площадь S основания исходной призмы. Таким образом, объем исходной призмы равен произведению S•h. Теорема доказана.
Слайд 29
Теоремы
Площадь боковой поверхности призмы равна произведению периметра ее
перпендикулярного сечения и длины бокового ребра.
Дано: АС1 - произвольная
n-угольная призма, a^AA1, A2B2C2D2 - перпендикулярное сечение (сечение призмы плоскостью, перпендикулярной боковому ребру), l - длина бокового ребра.
Доказать: Sбок = Р l, где Р - периметр перпендикулярного сечения.
Слайд 30
Теоремы
Доказательство.
Sбок=SAA1B1B + SBB1C1C + SCC1D1D +...
n слагаемых
Каждая
боковая грань призмы - параллелограмм, основание которого - боковое
ребро призмы, а высота - сторона перпендикулярного сечения.
Поэтому
Sбок=lA2B2+lB2C2+lC2D2+...=(A2B2+B2C2+C2D2+...)l=P l.
Sбок =Р l.
Теорема доказана.
Слайд 31
Теоремы
Площадь боковой поверхности прямой призмы равна произведению периметра
основания на высоту призмы.
Доказательство
Боковые грани
прямой призмы- прямоугольники, основания которых- стороны основания призмы, а высоты равны высоте h призмы. Площадь боковой поверхности призмы равна сумме площадей указанных прямоугольников, то есть равна сумме произведений сторон основания на высоту h. Вынося множитель h за скобки получим в скобках сумму сторон основания призмы, то есть его периметр P. Итак, Sбок=Ph. Теорема доказана.
Слайд 32
Задачи
Задача №1
Задача №2
Задача №3
Задача №4
Слайд 33
Задача №1
В прямоугольном параллелепипеде стороны основания равны
12см и 5см. Диагональ параллелепипеда образует с плоскостью основания
угол в 45˚. Найдите боковое ребро параллелепипеда.
A
B
C
D
K
L
M
N
Слайд 34
Задача №1
Рисунок с дополнительными построениями
Решение:
Рассмотрим прямоугольный ∆ABD
По
теореме Пифагора:
BD²=AD²+AB²
BD=√(AD²+AB²)=13
Рассмотрим ∆BLD-прямоугольный, равнобедренный, значит
BL=BD=13см
Ответ: BL=13см
A
K
B
C
D
L
M
N
12
5
Слайд 35
Задача №2
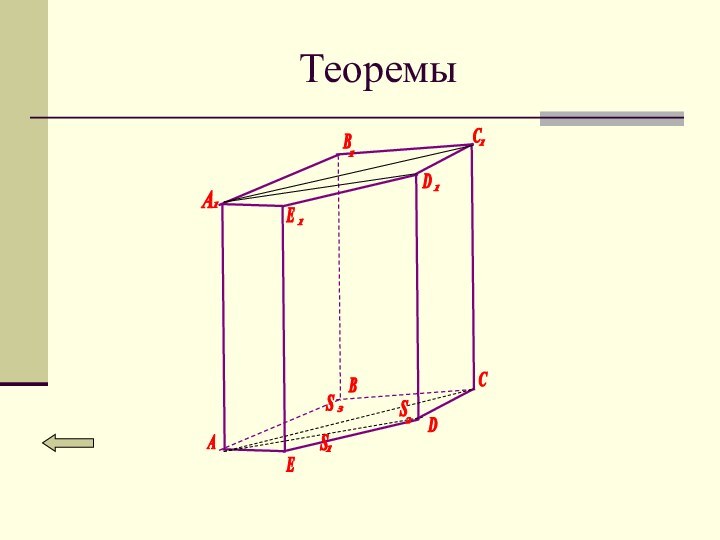
Высота прямой треугольной призмы ABCA1B2C3 равна
10. Расстояние от вершины A до плоскости A1BC равно
6. Найдите площадь сечения призмы плоскостью A1BC, если BC равен 16.
Слайд 36
Задача №2
Рисунок с дополнительными построениями
Решение:
Сечение A1BC разбивает
призму ABCA1B1C1 на две пирамиды AA1BC иA1BB1C1C. Пусть V–
объем призмы, V1- объем пирамиды AA1BC1, V2 - объем пирамиды A1BB1C1C. По свойству V=V1+V2 (1)
Проведем AM перпендикулярную BC, тогда A1M перпендикулярен BC. Обозначим AM=h, A1M=√100+h². Проведем MM1 AA1, тогда AM перпендикулярен MM1, значит AM перпендикулярен BB1C1, A1M1 AM → A1M1 перпендикулярен BB1C, A1M1=AM=h
M
M
1
Слайд 37
Задача №2
Найдем V, V1, V2.
V=SABC•AA1=½•16•h•10=80h
V1=⅓•SA1BC•AE= =⅓•½•16•(√100+h²)•6=16•(√100+h²)
V2=⅓•SBB1C1C•A1M1=⅔•16•h•10=160/3h
Найденные значения подставим
в формулу(1):
80h=16•(√100+h²)+160/3h
h=7,5
SABC=½•BC•A1M=½•16•(√100+56,25)=100
Ответ: S=100
Слайд 38
Задача №3
Дана прямая четырехугольная призма ABCDA1B1C1D1.
Расстояние от точек C до плоскости BC1D равно 3√2.
Плоскость BC1D наклонена к плоскости основания под углом 30˚. Найдите сторону основания призмы.
A
A
B
B
C
C
D
D
1
1
1
1
Слайд 39
Задача №3
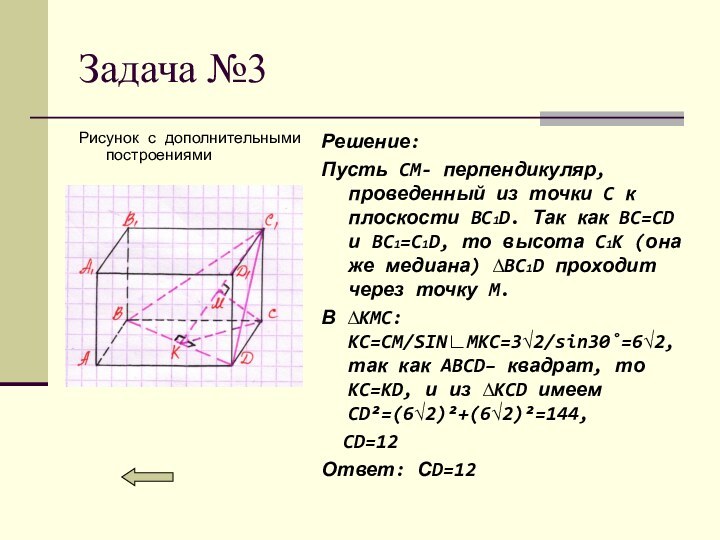
Решение:
Пусть CM- перпендикуляр, проведенный из точки C
к плоскости BC1D. Так как BC=CD и BC1=C1D, то
высота C1K (она же медиана) ∆BC1D проходит через точку M.
В ∆KMC: KC=CM/SIN∟MKC=3√2/sin30˚=6√2, так как ABCD– квадрат, то KC=KD, и из ∆KCD имеем CD²=(6√2)²+(6√2)²=144,
CD=12
Ответ: СD=12
Рисунок с дополнительными построениями
Слайд 40
Задача №4
Около правильной шестиугольной призмы описан цилиндр.
Площадь боковой поверхности цилиндра равна 16П√3. Расстояние между осью
цилиндра и диагональю боковой грани призмы равно 2√3. Найдите объем призмы.
A
B
A
A
A
A
A
B
B
B
B
B
3
1
2
2
3
4
4
1
5
5
6
6
Слайд 41
Задача №4
Рисунок с дополнительными построениями
Решение:
По формуле Sб ц=2ПRH=16П√3.
Отсюда RH=8√3. Расстояние d=2√3 есть расстояние между осью цилиндра
и плоскостью боковой грани призмы (так как OO1 A2A3B3B2). А это есть радиус вписанного в шестиугольник круга:
d=r=R√3/2=2√3
Отсюда R=4
Сторона основания правильной шестиугольной призмы A2A3=R=4. Высоту призмы H найдем из равенства RH=8√3; H=2√3
Sосн=6S∆OA2A3=6•(4²•√3|4)=24√3
Vпр=Sосн•H=24√3•2•√3=144
Ответ: Vпр=144