– мудрая кошка,
знает много историй.
Шишок компьютерный – гид
поисковикпо Интернету.
Гера – хозяин кошачьей семьи
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

























Гера – хозяин кошачьей семьи
Если а=0 и b=0,
то Х – любое число.
0*Х=0
Если ,
то X=-b/a.
Общий вид
ax+b=0
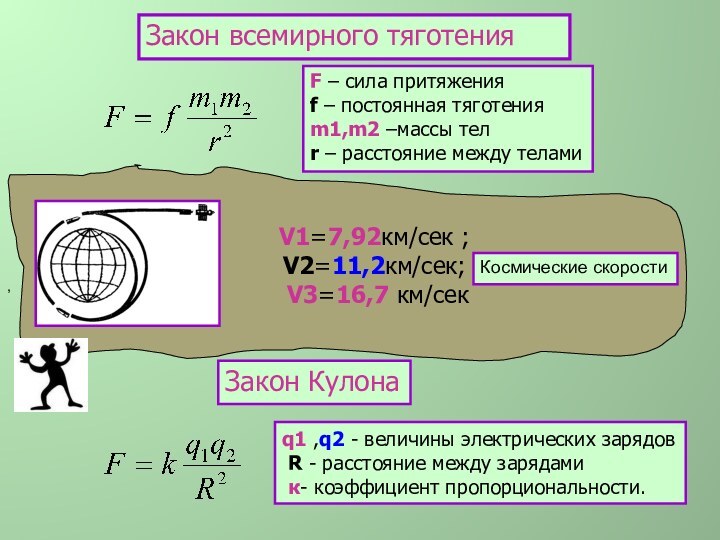
Закон Кулона
,
q1 ,q2 - величины электрических зарядов
R - расстояние между зарядами
к- коэффициент пропорциональности.
Космические скорости
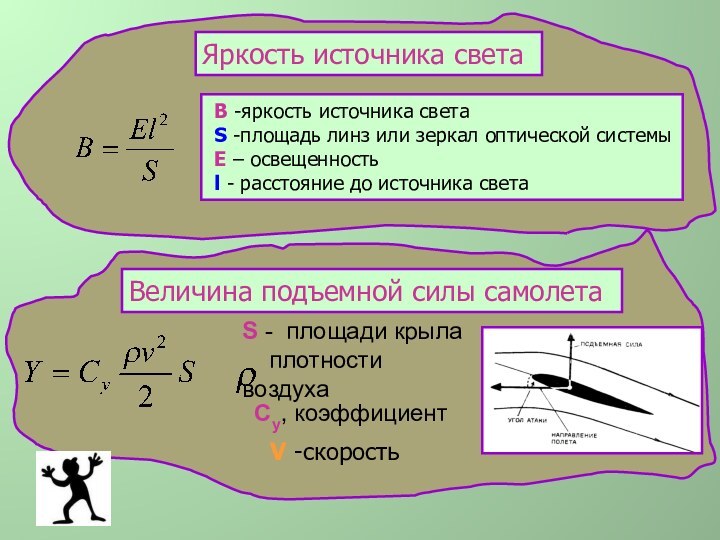
Величина подъемной силы самолета
S - площади крыла
плотности воздуха
Cy, коэффициент
V -скорость
Степень -3. Корни- 0;-6;1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
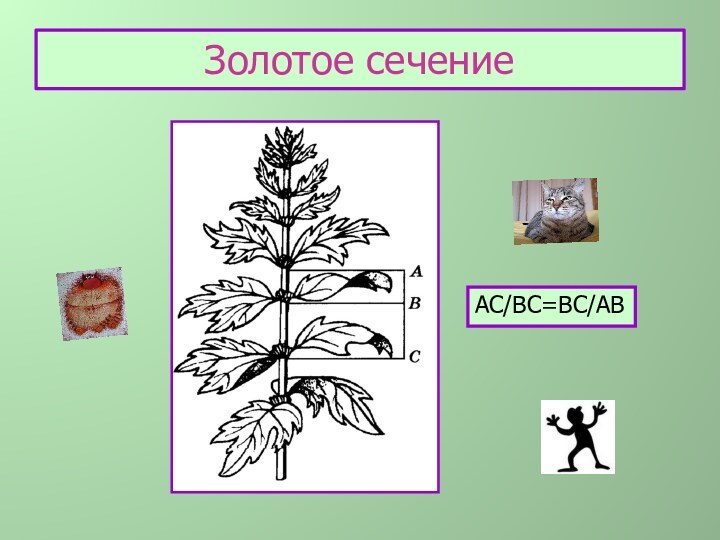
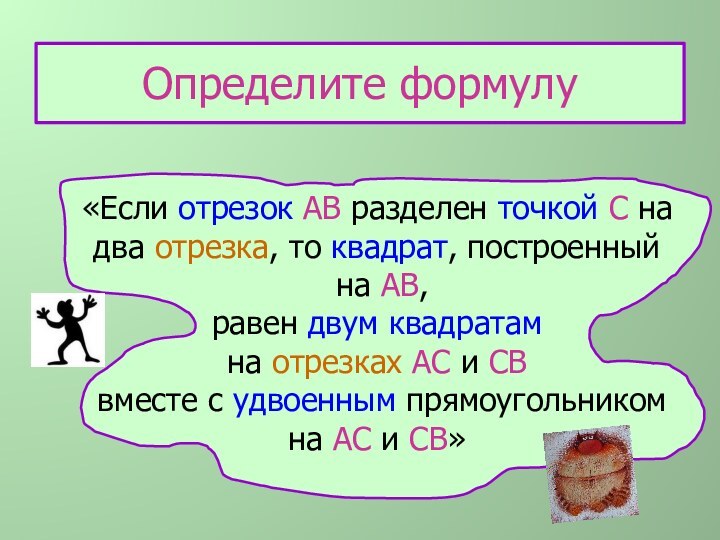
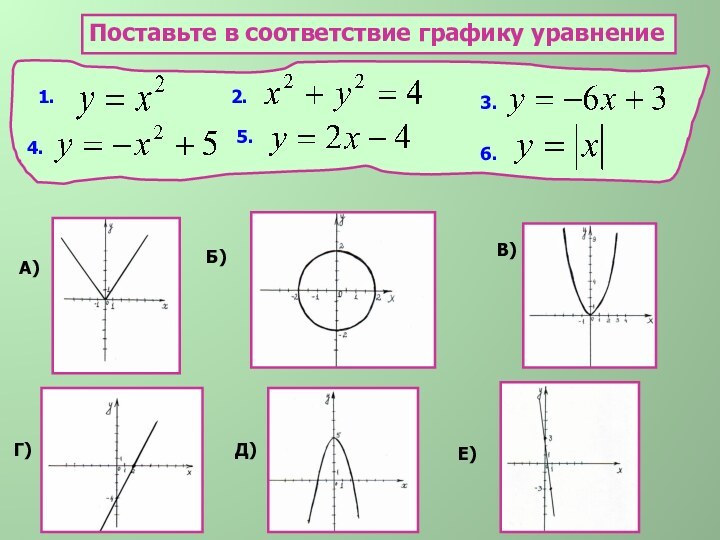
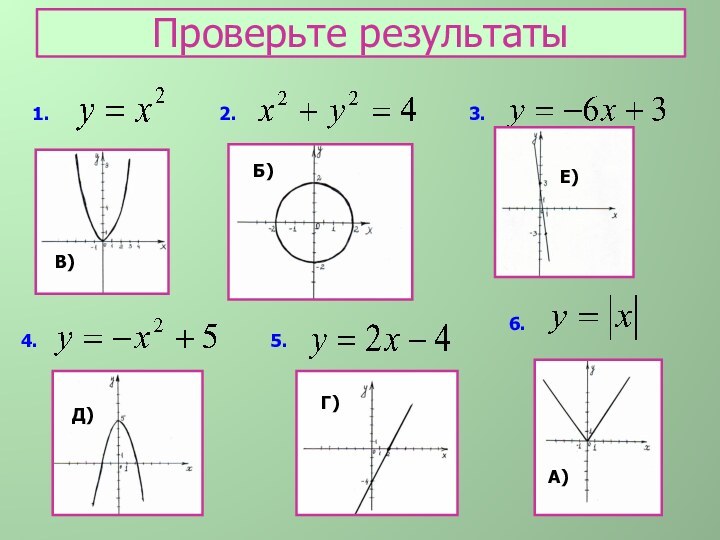
Определите формулу
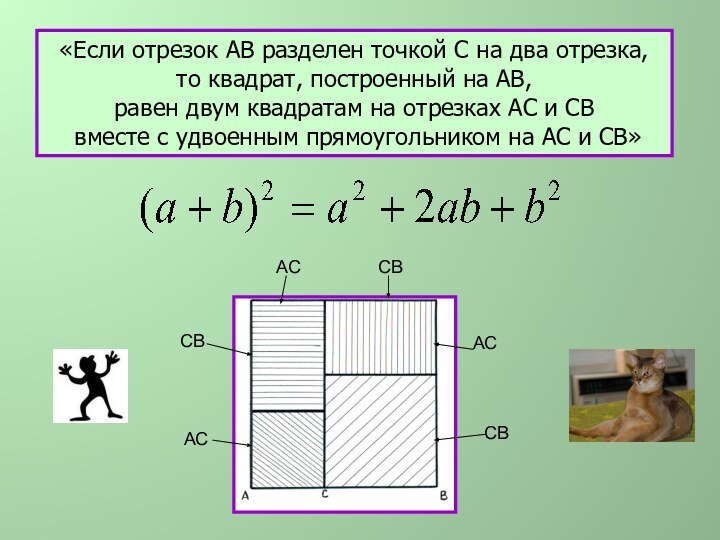
АС
СВ
АС
СВ
АС
СВ
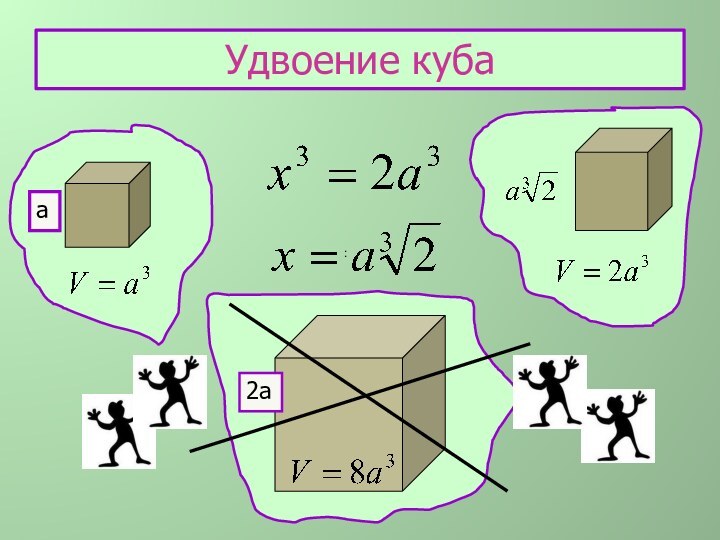
Задача
Задача
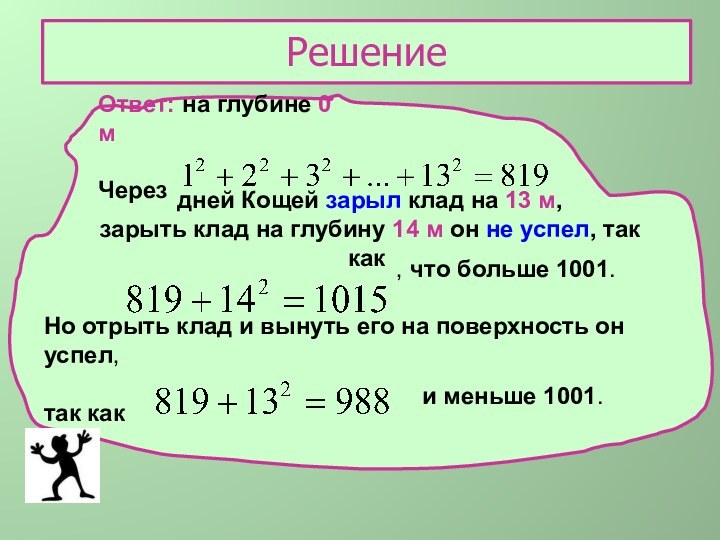
, что больше 1001.
Но отрыть клад и вынуть его на поверхность он успел,
так как
и меньше 1001.