- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Квадратные уравнения
Содержание
- 2. Содержание Определение квадратного уравнения;Решение неполных квадратных уравнений;Решение
- 3. Определение квадратного уравненияКвадратным уравнением называется уравнениеax2 +
- 4. Решение неполных квадратных уравнений(1)Примеры решения уравнений: Ответ:
- 5. Решение неполных квадратных уравнений (2)Уравнение ax2
- 6. Решение неполных квадратных уравнений (3)
- 7. Решение неполных квадратных уравнений(4)Примеры решения уравнений:2. x2
- 8. Решение неполных квадратных уравнений(5)1. x2 – x
- 9. Решение уравнений, сводящихся к неполным квадратным уравнениямРешите
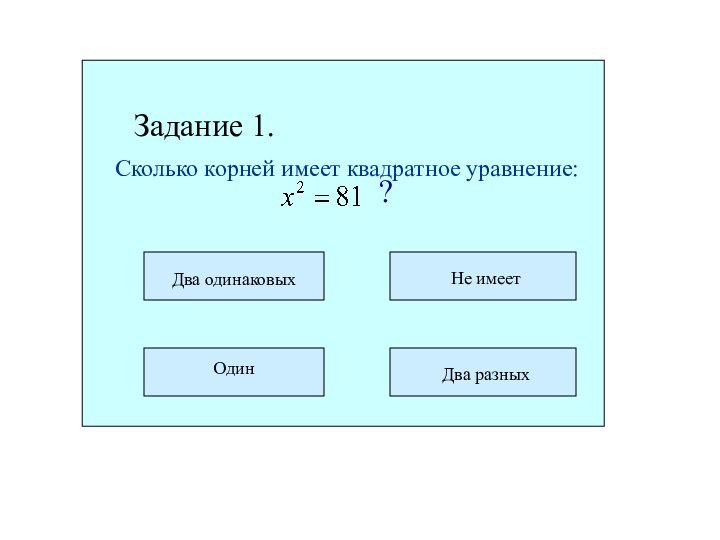
- 10. Задание 1.Сколько корней имеет квадратное уравнение:?
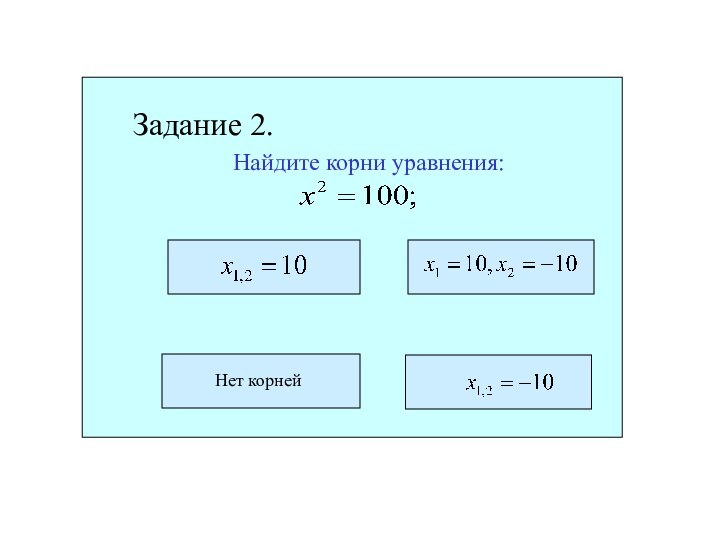
- 11. Найдите корни уравнения:Задание 2.
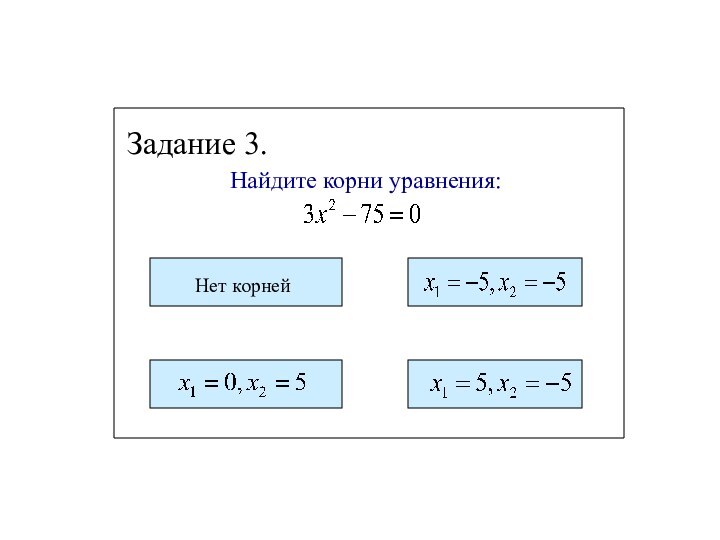
- 12. Задание 3.Найдите корни уравнения:
- 13. Задание 4.Найдите корни уравнения:
- 14. Ответ неверный!Повтори способ решения
- 15. Ответ неверный!Повтори способ решения
- 16. Ответ неверный !Повтори способ решения
- 17. Скачать презентацию
- 18. Похожие презентации











Слайд 2
Содержание
Определение квадратного уравнения;
Решение неполных квадратных уравнений;
Решение уравнений, сводящихся
к неполным квадратным уравнениям;
Слайд 3
Определение квадратного уравнения
Квадратным уравнением называется уравнение
ax2 + bx
+ c = 0,
где a, b, c- заданные числа,
a ≠ 0, x - неизвестноеПримеры квадратных уравнений:
1. - 0,25x2 + 0,5x +1= 0, a = - 0,25, b = 0,5; c = 1.
2. x2 + 3x – 1 = 0, a = 1. b = 3. c = -1.
3. -7x2 – 13x + 8 =0, a = -7, b = - 13, c = 8.
}
-полные квадратные уравнения
a ≠ 0, b ≠ 0, c ≠ 0.
4. -3x2 + 5x = 0, a = -3, b = 5, c = 0.
5. 4x2 – 81 = 0, a = 4, b = 0, c = 81
.
6. x2 = 0, a = 1, b = 0, c = 0.
}
- неполные квадратные уравнения
ax2 + bx = 0, b ≠ 0.
ax2 + c = 0, c ≠ 0.
ax2= 0.
Коэффициенты a, b, c квадратного уравнения называют так:
a – первый или старший коэффициент;
b – второй коэффициент;
c- свободный член.
Слайд 4
Решение неполных квадратных уравнений(1)
Примеры решения уравнений:
Ответ: x1
= 4, x 2 = - 4.
2. x2 =
3,
Ответ:
4. x2 = - 64,
Ответ: нет действительных корней, т. к. квадратный корень из отрицательного числа не извлекается.
Ответ:
1. x2 = 16,
( d < 0 )
Слайд 5
Решение неполных квадратных уравнений (2)
Уравнение ax2 =
0, где a ≠ 0, имеет два одинаковых корня
x1,2= 0.Пример решения уравнения:
1. 3x2 = 0;
- разделим обе части уравнения на 3,
:3
получим :
x2 = 0,
откуда
Ответ: x1,2= 0.
x1 = 0, x2 = 0;
Слайд 6
Решение неполных квадратных уравнений (3)
1. x2 – 16 = 0;
- разложим левую
часть уравнения по формуле разности квадратов: a2- b2= (a – b)(a+b); (x – 4)(x + 4) = 0,
- каждый множитель, записанный в скобках, приравняем нулю;
a) x - 4 = 0, b) x + 4 = 0,
- перенесем число из левой части уравнения в правую, изменив его знак на противоположный;
x1= 4;
x2 = - 4;
Ответ: x1 = 4, x2 = - 4.
Уравнение ax2 – c =0, где a ≠0, с≠0, имеет два разных корня.
Примеры решения уравнений:
-уравнение имеет два разных корня;
Слайд 7
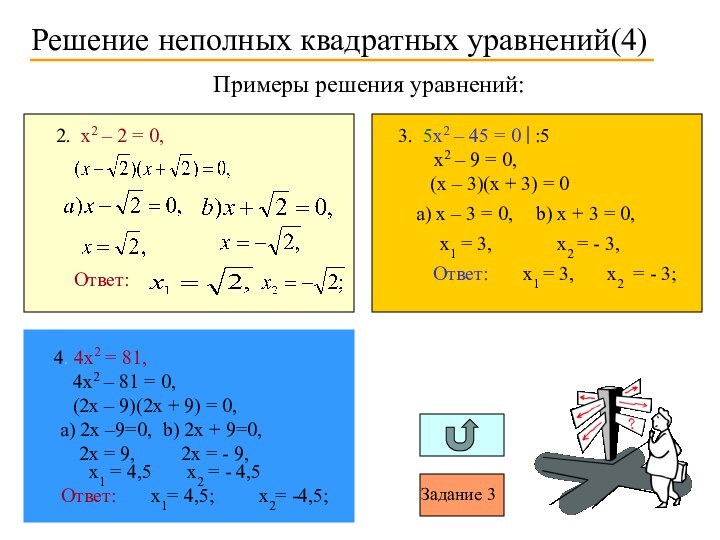
Решение неполных квадратных уравнений(4)
Примеры решения уравнений:
2. x2 –
2 = 0,
Ответ:
3. 5x2 – 45 = 0
x2 –
9 = 0, (x – 3)(x + 3) = 0
a) x – 3 = 0,
b) x + 3 = 0,
x1 = 3,
x2 = - 3,
Ответ:
x1 = 3,
x2 = - 3;
4. 4x2 = 81,
4x2 – 81 = 0,
(2x – 9)(2x + 9) = 0,
a) 2x –9=0,
b) 2x + 9=0,
x1 = 4,5
x2 = - 4,5
Ответ:
x1= 4,5;
x2= -4,5;
:5
2x = 9,
2x = - 9,
Слайд 8
Решение неполных квадратных уравнений(5)
1. x2 – x =
0,
- разложим левую часть уравнения на множители, вынеся за
скобку общий множитель; x(x – 1) = 0,
a) x = 0,
b) x - 1 = 0,
x = 1
Ответ: x1 = 0, x2 = 1;
Уравнение ax2 – bx = 0, где a ≠ 0, b ≠ 0, имеет два разных корня.
Примеры решения уравнения:
- каждый множитель приравняем нулю;
a·b = 0,
если
1. a = 0, b ≠ 0;
2. a ≠ 0, b = 0 ;
3. a = 0, b = 0;
Справка:
2. 3x2 = 5x,
3x2 – 5x = 0,
x(3x – 5) = 0,
a) x = 0,
b) 3x – 5 = 0,
3x = 5,
Ответ:
x1 = 0,
- решим простейшее линейное уравнение;
- уравнение имеет два разных корня;
Слайд 9
Решение уравнений,
сводящихся к неполным квадратным уравнениям
Решите уравнение:
- умножим
каждую часть уравнения на наименьщий общий знаменатель дробей;
·6
- сократим дроби; (4x2 – 3x)2 = (x2 + 5x)3,
- раскроем скобки;
12x2 – 6x = 3x2 + 15x,
- перенесем все члены уравнения из правой части уравнения в левую, изменив их знак на противоположный;
12x2 – 6x –3x2 – 15x = 0,
- приведем подобные;
9x2 – 21x = 0,
- разложим левую часть уравнения на множители;
3x(3x – 7) = 0,
- каждый множитель приравняем нулю,
a) 3x = 0 b) 3x – 7 = 0,
- решим эти линейные уравнения;
:3,
x = 0,
3x = 7
:3,
Ответ:
x1 = 0,