- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Квадратные уравнения 9 класс
Содержание
- 2. Посредством уравнений, теорем Я уйму всяких разрешал проблем. ( Чосер, английский поэт, средние века.)
- 3. Цель работы: Изучить тему «Квадратные уравнения».Исследовать зависимость между коэффициентами и корнями квадратного уравнения.
- 4. План работы: Изучить теорию вопроса:
- 5. Квадратным уравнением называется уравнение вида a x
- 6. Классификация .Квадратные уравнения.неполноеполноеа х ^ 2 +
- 7. «ДИСКРИМИНАНТ» - РАЗЛИЧИТЕЛЬ.Д = в^2 - 4
- 8. Приёмы устного решения квадратных уравнений.a x ^2
- 9. 3. Если a = c, b =
- 10. Теорема Виета. Если х1 и х2 корни
- 11. Исследование знаков корней квадратного уравнения х^2
- 12. Ситуации, в которых может использоваться теорема Виета.
- 13. Методы решения полных квадратных уравнений.ax^2 + bx
- 14. Методы решения уравнений, сводящихся к квадратным.af^2(x) +
- 15. Штифель (1486 – 1567) в 1544 году
- 16. Литература. Алгебра. 8 класс. Под редакцией Теляковского
- 17. Скачать презентацию
- 18. Похожие презентации
















Слайд 3
Цель работы:
Изучить тему «Квадратные уравнения».
Исследовать зависимость между
коэффициентами и корнями квадратного уравнения.
Слайд 4
План работы:
Изучить теорию вопроса:
Квадратные уравнения. Виды квадратных уравнений.
Методы решения
квадратных уравнений.Зависимость между корнями и коэффициентами
квадратного уравнения.
Приёмы рационального решения
квадратных уравнений, используя
свойства коэффициентов.
Слайд 5 Квадратным уравнением называется уравнение вида a x ^
2 + b x + c = 0
где х
– переменная, a, b и c – некоторые числа, причём а ≠ 0.
a x^2 + b x + c = 0
Первый коэффициент
Второй коэффициент
Свободный
член
Слайд 6
Классификация .
Квадратные уравнения.
неполное
полное
а х ^ 2 + в
х + с = 0
приведённое
x ^ 2 + p
x + q = 0c = 0;
a x ^ 2 + b x = 0
b = 0; c = 0;
a x ^ 2 = 0
b = 0;
a x ^ 2 + c = 0
Слайд 7
«ДИСКРИМИНАНТ» - РАЗЛИЧИТЕЛЬ.
Д = в^2 - 4 а
с
Д > 0
Д = 0
Д < 0
Уравнение имеет
два
действительныхкорня.
Уравнение имеет
два равных
действительных корня.
Уравнение не имеет
корней.
х1 = (- в- √ Д )/ 2а;
х 2= (- в + √ Д )/2а
х1,2 = - в / 2а
Слайд 8
Приёмы устного решения квадратных уравнений.
a x ^2 +
b x + c = 0.
Основа:
f (x) = a x ^2 + b x + c ;f (1) = a + b + c; f (- 1) = a - b + c.
1.Если a + b + c = 0, то один корень уравнения x = 1, а второй x = c/a.
2.Если a - b + c = 0, то один корень уравнения x = - 1, а второй x = - c/a.
Слайд 9 3. Если a = c, b = a^2
+ 1, то один корень уравнения x = -
a, а второй x = -1/a.4. Если a = c, b = -(a^2 + 1), то один корень уравнения x = a, а второй x = 1/a.
Слайд 10
Теорема Виета.
Если х1 и х2 корни приведённого
квадратного
уравнения х^2 + px + q =
0 , то x1 + x2 = - p, а x1 x2 = q.
Обратное утверждение:
Если числа m и n таковы, что m + n = - p, mn = q, то эти числа являются корнями уравнения х^2 + px + q = 0.
Обобщённая теорема:
Числа х1 и х2 являются корнями приведённого квадратного уравнения х^2 + px + q = 0 тогда и только тогда, когда x1 + x2 = - p, x1 x2 = q.
Следствие: х^2 + px + q = (х – х1)(х – х2)
Слайд 12
Ситуации, в которых может
использоваться теорема Виета.
Проверка
правильности найденных корней.
Определение знаков корней квадратного уравнения.
Устное
нахождение целых корней приведённого квадратного уравнения.Составление квадратных уравнений с заданными корнями.
Разложение квадратного трёхчлена на множители.
Слайд 13
Методы решения полных квадратных уравнений.
ax^2 + bx +
c = 0
Теорема Виета:
x1 + x2 = -b/a,
х1 x2
= c/aОбщая формула корней:
x1,2 = (-b ± √b^2 – 4ac)/2a
Если a – b + c = 0,
то x1 = - 1; x2 = - c/a.
Если a ± b + c ≠ 0,
то решить уравнение
x^2 + bx + c = 0
и разделить полученные
корни на a.
Если a + b + c = 0,
то x1 = 1; x2 = c/a.
Общая формула с чётными
коэффициентами:
х1,2 = (-b/a ± √(b/2)^2 – ac)/a
Слайд 14
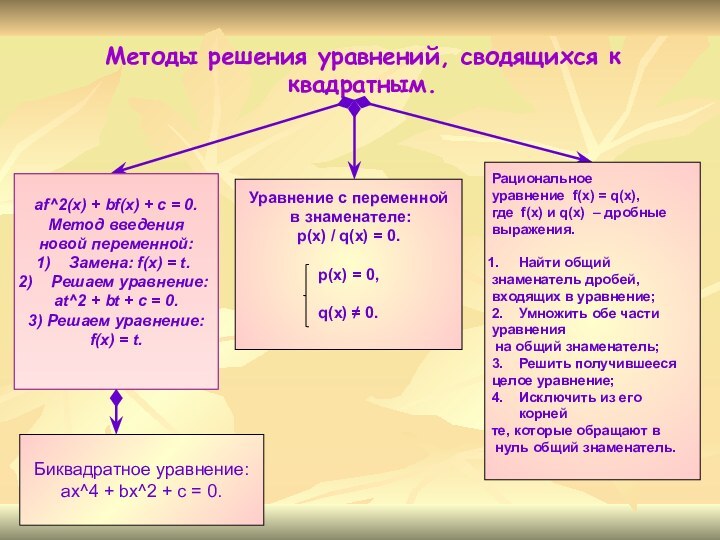
Методы решения уравнений, сводящихся к квадратным.
af^2(x) + bf(x)
+ c = 0.
Метод введения
новой переменной:
Замена: f(x) =
t.Решаем уравнение:
at^2 + bt + c = 0.
3) Решаем уравнение:
f(x) = t.
Биквадратное уравнение:
ax^4 + bx^2 + c = 0.
Уравнение с переменной
в знаменателе:
p(x) / q(x) = 0.
p(x) = 0,
q(x) ≠ 0.
Рациональное
уравнение f(x) = q(x),
где f(x) и q(x) – дробные
выражения.
Найти общий
знаменатель дробей,
входящих в уравнение;
2. Умножить обе части
уравнения
на общий знаменатель;
3. Решить получившееся
целое уравнение;
4. Исключить из его корней
те, которые обращают в
нуль общий знаменатель.
Слайд 15 Штифель (1486 – 1567) в 1544 году сформировал
общее правило решения квадратных уравнений, приведённых к единому каноническому
видуx^2 + bx = c
при всевозможных комбинациях знаков и коэффициентов b и c.
Франсуа Виет (1540 – 1603) вывел формулы решения квадратного уравнения в общем виде, однако он признавал только положительные числа.
Итальянские учёные Тарталья, Кардано, Бомбелли среди первых в XVI веке учитывают, помимо положительных, и отрицательные корни.
В XVII веке благодаря трудам Жиррара, Декарта, Ньютона и других учёных, способ решения квадратных уравнений принимает современный вид.
Слайд 16
Литература.
Алгебра. 8 класс. Под редакцией Теляковского С.
А.
М., Просвещение, 2002 г.Сборник задач по алгебре. Галицкий М. Л., Гольдман А. М.,
Звавич Л. И. М., 1996 г.
3. Алгебра.Дополнительные главы к школьному учебнику 8 класса. Макарычев Ю. Н., Миндюк Н. Г.
М., Просвещение, 2003 г.