- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Квадратные уравнения и уравнения, приводимые к квадратным
Содержание
- 2. Расписание1. Алгебра2. История3. География4. Рисование
- 3. Алгебра
- 4. Выбрать лишнее уравнение: 1. 3х2−х-7
- 5. Найдите в каждой группе уравнений «лишнее»:
- 6. Найдите корни: а) х²-49 =
- 7. Какие из уравнений
- 8. Как называется выражение b² - 4ac ? Что показывает значение данного выражения?
- 9. Решите данные уравнения: 2х²+3х-5=0 3х²+х+1=0 4х²-4х+1=0
- 10. Всегда ли полные квадратные уравнения
- 11. История
- 12. История развития квадратных
- 13. Квадратные уравнения в Багдаде (9 век):Впервые квадратные
- 14. Квадратные уравнения в Древнем Вавилоне:Необходимость решать
- 15. Квадратные уравнения в ИндииЗадачи на квадратные уравнения
- 16. Квадратные уравнения в Европе в 13-17 веках:Формулы
- 17. География
- 18. Географические названия столиц зарубежных стран употребляются
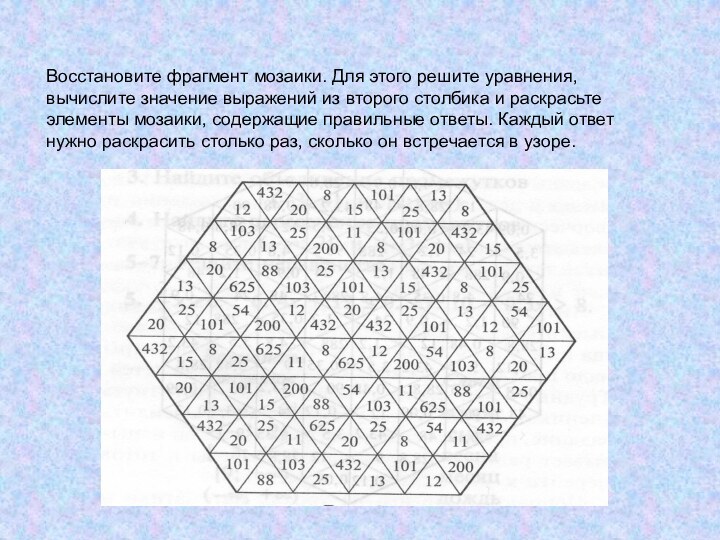
- 20. Рисование
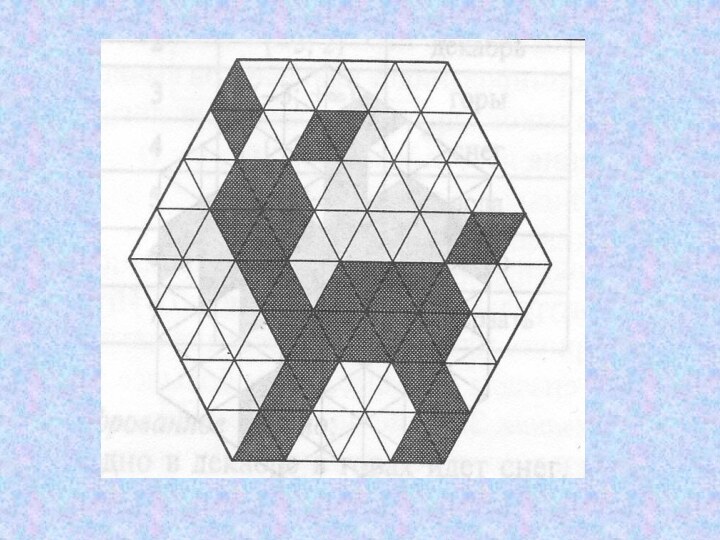
- 21. Восстановите фрагмент мозаики. Для этого решите уравнения,
- 23. Скачать презентацию
- 24. Похожие презентации
Расписание1. Алгебра2. История3. География4. Рисование




















Слайд 5
Найдите в каждой группе уравнений «лишнее»:
А:
1. 3х2−х = 0,
Б: 1. х2 −7х +1=0,2. х2 −25 = 0, 2. 7х2 − 4х +8 = 0,
3. 4х2 + х −3 = 0, 3. х2 + 4х −4 = 0,
4. 4х2 = 0. 4. х2 −5х −3 = 0.
Слайд 6
Найдите корни:
а) х²-49 = 0;
б) х·(х +
0,7) = 0;в) х2 − 4х = 0;
г) 16х2 −1 = 0;
д) 4,5 х2 = 0.
Слайд 7 Какие из уравнений не
имеют
корней:
1. х2 −1 = 0;2. (х −3)² = 0;
3. (х −4)² + 6 = 0;
4. х + 4 = 0;
5. х2 + 7 = 0.
Слайд 10 Всегда ли полные квадратные уравнения можно
решить только через дискриминант?
Подберите корни следующих уравнений:
Х² +2х -24 =0Х² - 6х +8 =0
Х² +9х +14 =0
Слайд 12
История развития квадратных
уравнений:
Квадратные уравнения в Багдаде(9 век).
Квадратные уравнения в Древнем
Вавилоне. Квадратные уравнения в Индии.
Квадратные уравнения в Европе 13 -17в.в.
Слайд 13
Квадратные уравнения в Багдаде (9 век):
Впервые квадратные уравнения
появились
в городе Багдаде, их вывел приглашённый математик из Хорезм(Ныне
территория Узбекистана) Мухаммед бен-Муса Ал-Хорезми. В отличие от греков, решавших квадратные уравнения геометрическим путем, он мог решить любые квадратные уравнения по общему правилу (найти положительные корни). Если у греков было геометрическое решение, то метод Ал-Хорезми почти алгебраический.
Слайд 14
Квадратные уравнения в Древнем Вавилоне:
Необходимость решать уравнения
не только первой, но и второй степени ещё в
древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а так же с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до нашей эры вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения: х2 + х = х2 ─ х =Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены, Несмотря на высокий уровень развития алгебры в Вавилонии, в клинописных текстах отсутствует понятие отрицательного числа и общие методы решения квадратных уравнений.
Слайд 15
Квадратные уравнения в Индии
Задачи на квадратные уравнения встречаются
уже в 499 году.
В Древней Индии были распространены публичные
соревнования в решении трудных задач.В одной из старинных индийских книг говорится по поводу таких соревнований следующее: “Как солнце блеском своим затмевает звёзды, так учёный человек затмит славу другого в народных собраниях, предлагая и решая алгебраические
задачи”.
Слайд 16
Квадратные уравнения в Европе в 13-17 веках:
Формулы решения
квадратных уравнений в Европе были
Впервые изложены в 1202
году итальянским математикомЛеонардо Фибоначчи.
Общее правило решения квадратных
уравнений, приведенных к единому
каноническому виду аx2 + bx + c = 0,было
Сформулировано в Европе лишь в 1544
Году немецким математиком
Михаэлем Штифелем.
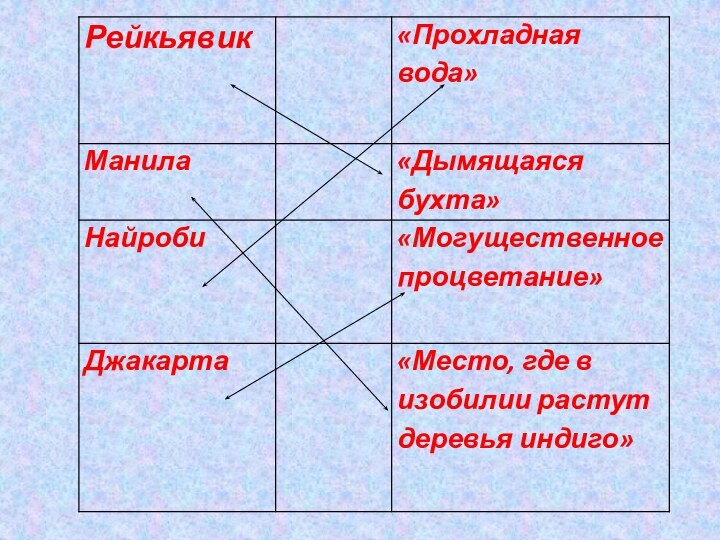
Слайд 18 Географические названия столиц зарубежных стран употребляются без
перевода на русский язык. Например, столицу Ирландии – Dublin,
мы называем Дублин, даже не задумываясь, что при дословном переводе это название означает – «тёмная заводь».Решите уравнения. По совпадающим множествам решений соедините
названия столиц с их дословным переводом.