Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Лекции по комплексным числам

Содержание

2. Лекция 1Комплексные числа: определение;геометрическое изображение комплексного числа; формы записи комплексного числа; операции над комплексными числами.
3. Решить уравнение: Решение:
4. Определение. Комплексным числом называется выражение вида
5. Алгебраическая форма записи комплексного числа1. Два комплексных
6. -33 Такая форма записи комплексного числа называется
7. -33 Геометрическое изображение комплексного числа
8. -33 Геометрическое изображение комплексного числа
9. -33 Геометрическое изображение комплексного числа
10. Тригонометрическая форма записи комплексного числаImzRezyφrzx
11. Показательная форма записи
12. (1707-1783) Леонард Эйлер принадлежит к числу гениев,
13. Показательная форма записи
14. Пример. z=-1-i записать в тригонометрической и показательной формах. Решение.
15. Операции над комплексными числами z0=x0+iy0 и
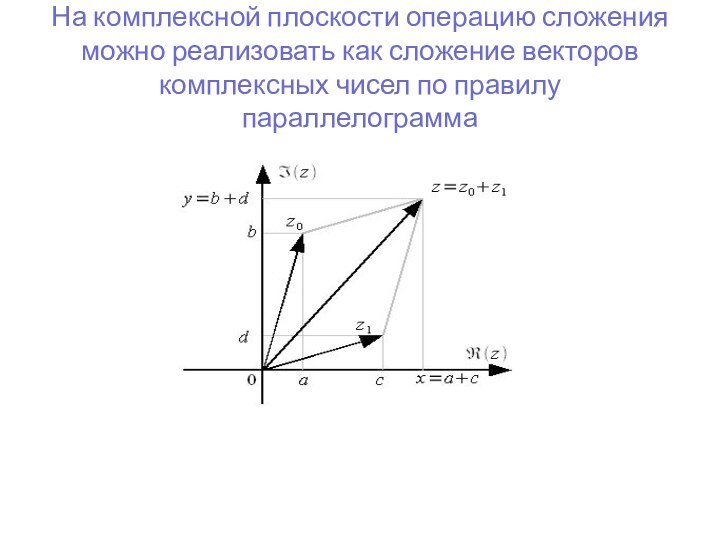
16. На комплексной плоскости операцию сложения можно реализовать как сложение векторов комплексных чисел по правилу параллелограмма
17. Разность двух комплексных чисел и есть также
18. Расстояние между двумя точками:
19. 3. Умножение комплексных чисел. Для того чтобы
20. 4. Деление комплексных чисел Пример
21. Скачать презентацию
22. Похожие презентации

Лекция 1Комплексные числа: определение;геометрическое изображение комплексного числа; формы записи комплексного числа; операции над комплексными числами.

Главная
Математика
Лекции по комплексным числам

Мария АльбертовнаЗироянПрофессор кафедры математики и информатики Лекции по математике для студентов экономических специальностей

Лекция 1Комплексные числа: определение;геометрическое изображение комплексного числа; формы записи комплексного числа; операции над комплексными числами.

Определение. Комплексным числом называется выражение вида где

Алгебраическая форма записи комплексного числа1. Два комплексных числа

-33 Такая форма записи комплексного числа называется алгебраической.Изображается комплексное число точкой на

-33 Геометрическое изображение комплексного числа Для геометрического представления комплексных

-33 Геометрическое изображение комплексного числа

Тригонометрическая форма записи комплексного числаImzRezyφrzx

(1707-1783) Леонард Эйлер принадлежит к числу гениев, чье творчество стало достоянием всего

Пример. z=-1-i записать в тригонометрической и показательной формах. Решение.

Операции над комплексными числами z0=x0+iy0 и z1=x1+iy1Сумма двух комплексных чисел и

На комплексной плоскости операцию сложения можно реализовать как сложение векторов комплексных чисел по правилу параллелограмма

Разность двух комплексных чисел и есть также комплексное число:

3. Умножение комплексных чисел. Для того чтобы получить формулу для умножения комплексных

5. Операции над комплексными числами, заданными в тригонометрической форме. 1.

Слайды презентации

Слайд 2 Лекция 1
Комплексные числа:
определение;
геометрическое изображение комплексного числа;
формы

записи комплексного числа;
операции над комплексными числами.

Слайд 3 Решить уравнение: Решение:

Слайд 4 Определение. Комплексным числом называется выражение вида где

- действительные числа ,

мнимая единица. Число действительная часть комплексного числа и обозначается , а мнимая часть и обозначается , т.е.

Слайд 5 Алгебраическая форма записи комплексного числа
1. Два комплексных числа

равны, если

2. Z = 0, если x=0; y=0

3. Если y=0, то z R.

4. Числа называются
сопряженными и обозначаются

Слайд 6 -3
3
Такая форма записи комплексного числа называется алгебраической.
Изображается

-33 Такая форма записи комплексного числа называется алгебраической.Изображается комплексное число точкой

комплексное число точкой на комплексной плоскости.

. z1

. z2

. z4

. z3

Rez

Imz

Слайд 7 -3
3
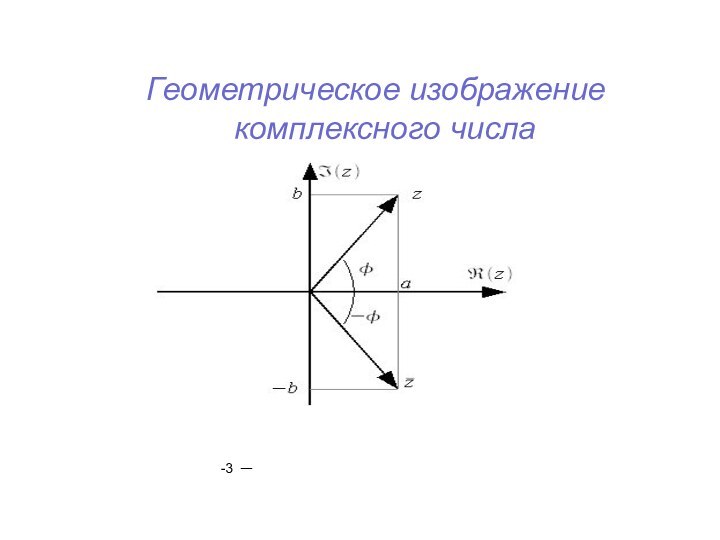
Геометрическое изображение комплексного числа

-33 Геометрическое изображение комплексного числа Для геометрического представления комплексных чисел

Для геометрического представления комплексных чисел служат точки координатной плоскости

OXY.
Плоскость называется комплексной , если каждому комплексному числу соответствует точка плоскости , причем это соответствие взаимно однозначно.
Оси OX и OY, на которых расположены действительные числа
и чисто мнимые числа
, называются соответственно действительной и мнимой осями.

Слайд 8 -3
3
Геометрическое изображение комплексного числа

Слайд 9 -3
3
Геометрическое изображение комплексного числа

Для геометрического представления комплексных чисел служат точки координатной плоскости

Слайд 10 Тригонометрическая форма записи комплексного числа
Imz
Rez
y
φ
r
z
x

Слайд 11 Показательная форма записи

комплексных чисел Из формулы Эйлера

Слайд 12 (1707-1783)
Леонард Эйлер принадлежит к числу гениев, чье

(1707-1783) Леонард Эйлер принадлежит к числу гениев, чье творчество стало достоянием

творчество
стало достоянием всего человечества. Открытия Эйлера в
математике,

механике, физике и технике прочно вошли в
современную науку. Многие из них были сделаны в
Петербургской Академии наук, где Леонард Эйлер
проработал 31 год (в 1727-1741 гг. и 1766-1783 гг.).

Слайд 13 Показательная форма записи

комплексных чисел Из формулы Эйлера

Слайд 14 Пример. z=-1-i записать в тригонометрической и показательной формах. Решение.

Слайд 15 Операции над комплексными числами z0=x0+iy0 и z1=x1+iy1
Сумма двух

комплексных чисел и есть также комплексное число :z0 +

z1 =(x0+x1)+i(y0+y1)
Пример: (3+2i)+(1+5i)=(3+1)+i(2+5)=4+7i.
Как следует из выражения при сложении реальные и мнимые части комплексного числа также складываются.

Слайд 16 На комплексной плоскости операцию сложения можно реализовать как

сложение векторов комплексных чисел по правилу параллелограмма

Слайд 17 Разность двух комплексных чисел и есть также комплексное

Разность двух комплексных чисел и есть также комплексное число: z0

число:
z0 - z1 =(x0-x1)+i(y0-y1).
Пример:

(4+i)-(-2-i)=(4+2)+i(1+1)=6+2i.
На комплексной плоскости операцию
вычитания можно реализовать как
вычитание векторов комплексных
чисел по правилу параллелограмма .
На первом шаге из вектора
формируется вектор ,
после чего вектор складывается
с вектором по правилу параллелограмма.

2.Вычитание комплексных чисел

Слайд 18 Расстояние между двумя точками:

Слайд 19 3. Умножение комплексных чисел. Для того чтобы получить формулу

3. Умножение комплексных чисел. Для того чтобы получить формулу для умножения

для умножения комплексных чисел необходимо перемножить два комплексных числа

по правилу умножения многочленов: z1 · z2=(x1x2-y1y2)+i(x1y2+x2y1). Пример 1. (1+3i)(-5-2i)=-5-15i-2i-6i2 =-5-17i+6= =1-17i . Пример 2. (1+3i)(1-3i)=1-3i+3i-9i2 =1+9=10 . всегда действительное число