- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Лекція 5. Поверхні. Класифікація поверхонь. Точки на поверхні
Содержание
- 2. Геометричне тіло - замкнута частина
- 3. ЗОБРАЖЕННЯ БАГАТОГРАННИКІВ
- 4. ВИДИ БАГАТОГРАННИКІВПіраміди, призми, призматоїди
- 5. КРЕСЛЕННЯ БАГАТОГРАННИКІВ Побудова креслеників багатогранників
- 6. Належність точки і прямої поверхні багатогранникаНалежність точок і прямих поверхні багатогранниказнаходиться як належність точок до прямої.
- 8. Сукупність геометричних елементів та умов, необхідних і
- 9. КІНЕМАТИЧНЕ УТВОРЕННЯ ПОВЕРХНІlТвірнаНапрямнаmРодина твірних і родина
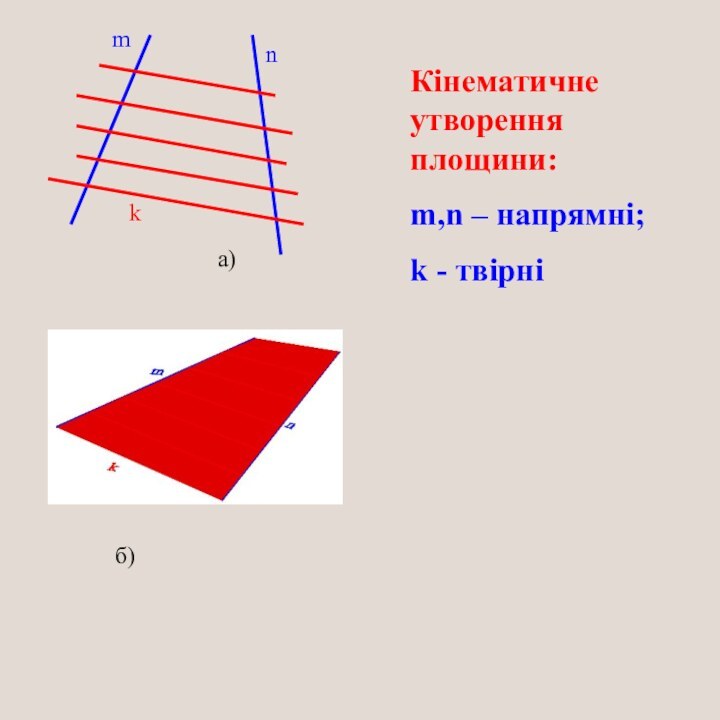
- 10. а)б)Кінематичне утворення площини:m,n – напрямні;k - твірніmnk
- 11. Кінематичне утворення конічної поверхні:SmkКонічна поверхня утворюється таким
- 12. Циліндрична поверхня утворюється переміщенням прямолінійної твірної (k)
- 13. ВИЗНАЧНИК ПОВЕРХНІСукупність основних параметрів поверхні які визначають
- 14. Циліндр обертання може бути утворений обертанням прямої
- 15. За СПОСОБОМ УТВОРЕННЯ поверхні поділяються на такі
- 16. 5. РОЗГОРТНІ ЛІНІЙЧАТИ ПОВЕРХНІЛінійчатою називають поверхню, утворену
- 17. ПОВЕРХНІ ОБЕРТАННЯПоверхні обертання утворюються обертанням певної лінії
- 18. паралельгорловинаГоловний меридіан (січ. пл.Σ)
- 19. СФЕРА - поверхня, яка утворюється обертанням кола
- 20. При обертанні кола (або її дуги) навколо
- 21. 8. ГВИНТОВІ ПОВЕРХНІПохилий гелікоїд – утворений рухом
- 22. Якщо висота напрямного конусу зменшується, то в
- 24. 10. НАЛЕЖНІСТЬ ТОЧКИ І ПРЯМОЇ КРОВОЇ ПОВЕРХНІПрямий круговий циліндр
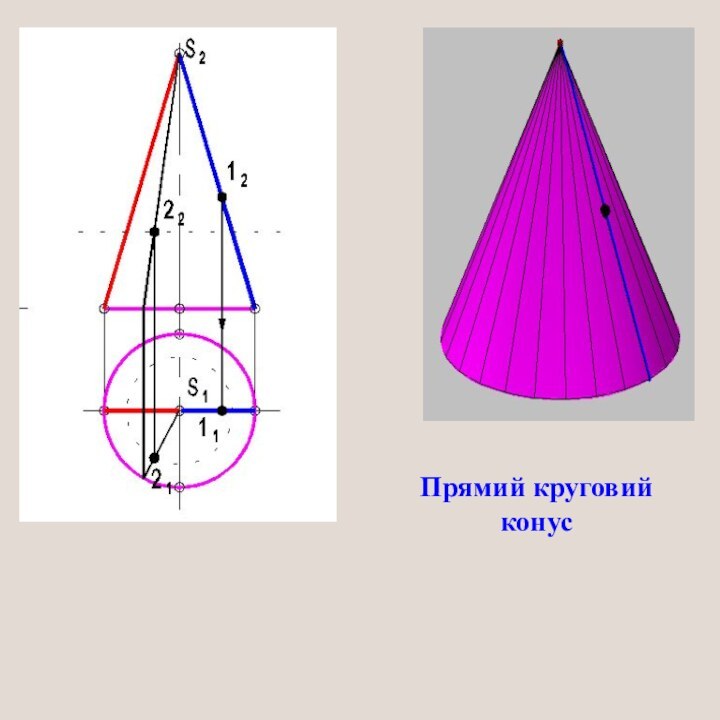
- 25. Прямий круговий конус
- 26. 1. Ввести площину Σ перпендикулярну до осі
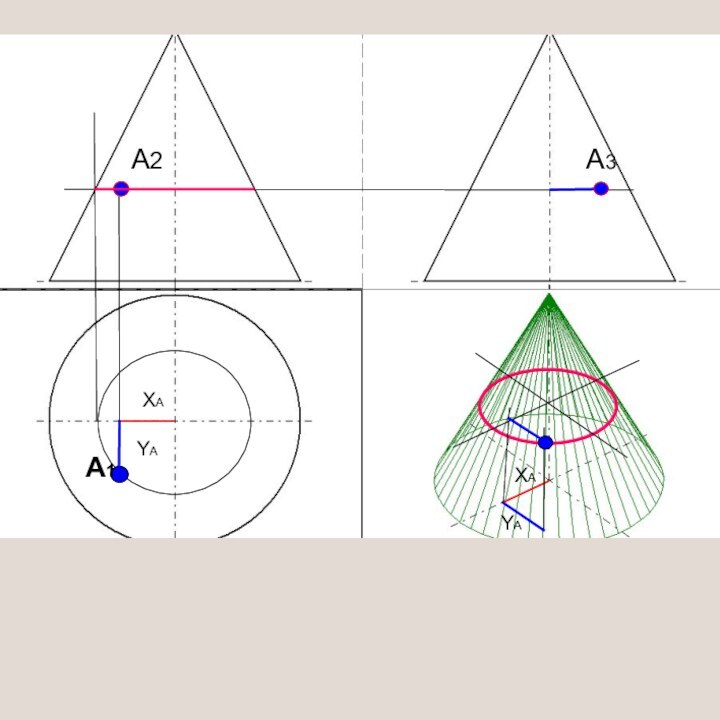
- 27. YAA1A2A3XAYAXAYA
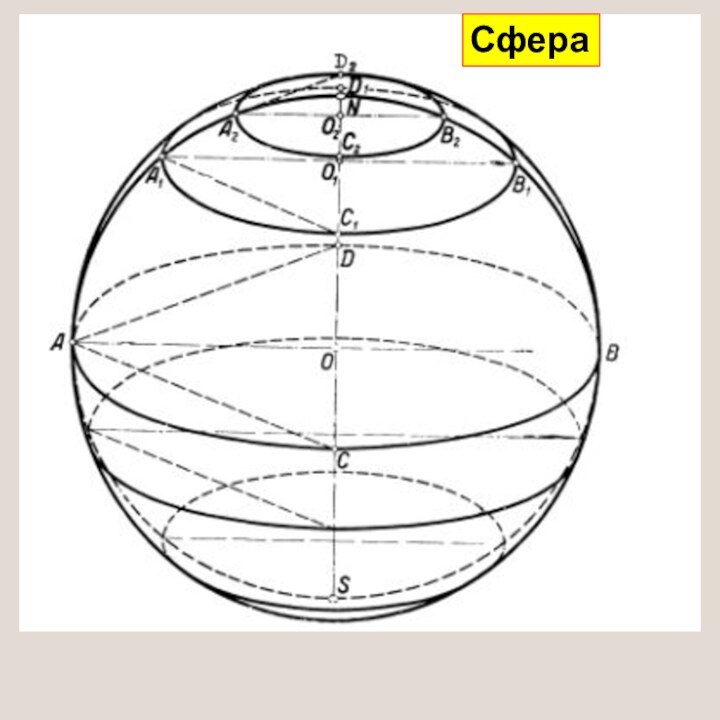
- 28. Сфера
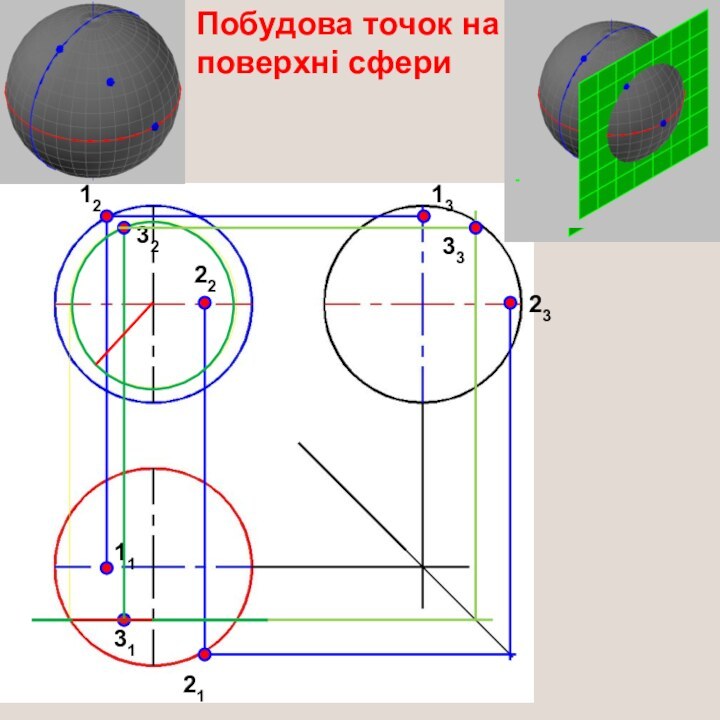
- 29. Побудова точок на поверхні сфери121113222123313233
- 31. Скачать презентацию
- 32. Похожие презентации










Слайд 5
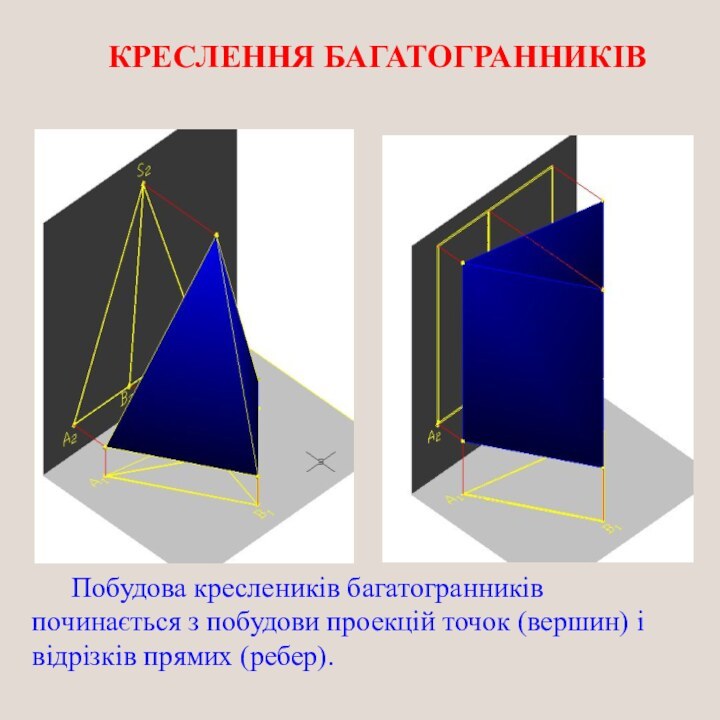
КРЕСЛЕННЯ БАГАТОГРАННИКІВ
Побудова креслеників багатогранників
починається
з побудови проекцій точок (вершин) і відрізків прямих (ребер).
Слайд 6
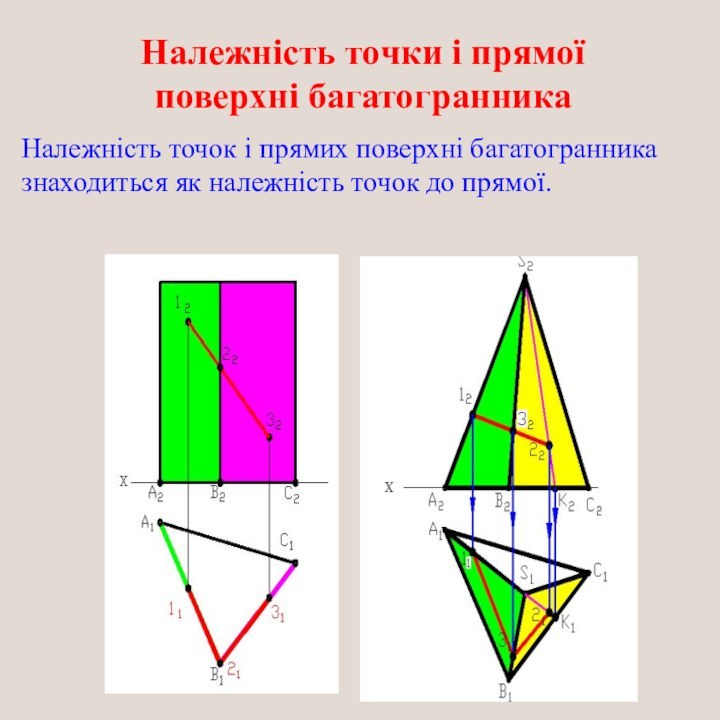
Належність точки і прямої поверхні багатогранника
Належність точок і
прямих поверхні багатогранника
знаходиться як належність точок до прямої.
Слайд 7 В
НГ поверхню розглядають як множину послідовних положень лінії, що
рухається у просторі. Лінію, яка рухається у просторі називають ТВІРНОЮ. Твірні можуть бути прямими або кривими, зберігати або змінювати свою форму під час руху. Закон руху твірної також може бути різним: вона може рухатися вздовж певних прямих, або кривих ліній, які називають НАПРЯМНИМИ. Такий принцип утворення поверхні називають КІНЕМАТИЧНИМ.2. УТВОРЕННЯ ТА ЗАВДАННЯ
ПОВЕРХНІ
Слайд 8
Сукупність геометричних елементів та
умов, необхідних і достатніх
для задання
поверхні, називається її визначником.
Визначник кінематичної поверхні складають:
твірна;
напрямні елементи;умови змінення положення та форми твірної під час руху, які задають його алгоритмічну частину.
Сукупність положень твірної складає лінійчатий каркас поверхні. Така поверхня неперервна.
Слайд 9
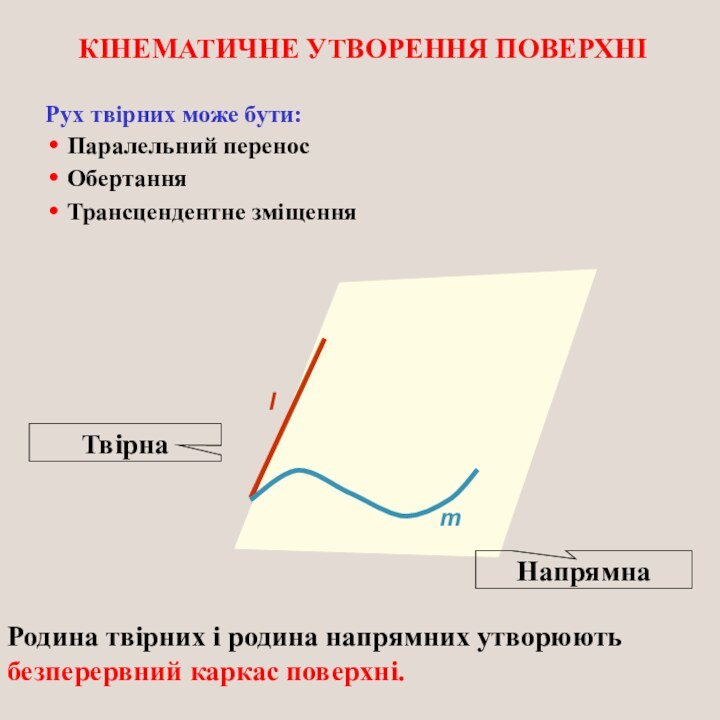
КІНЕМАТИЧНЕ УТВОРЕННЯ ПОВЕРХНІ
l
Твірна
Напрямна
m
Родина твірних і родина напрямних
утворюють безперервний каркас поверхні.
Рух твірних може бути:
Паралельний перенос
Обертання
Трансцендентне зміщення
Слайд 11
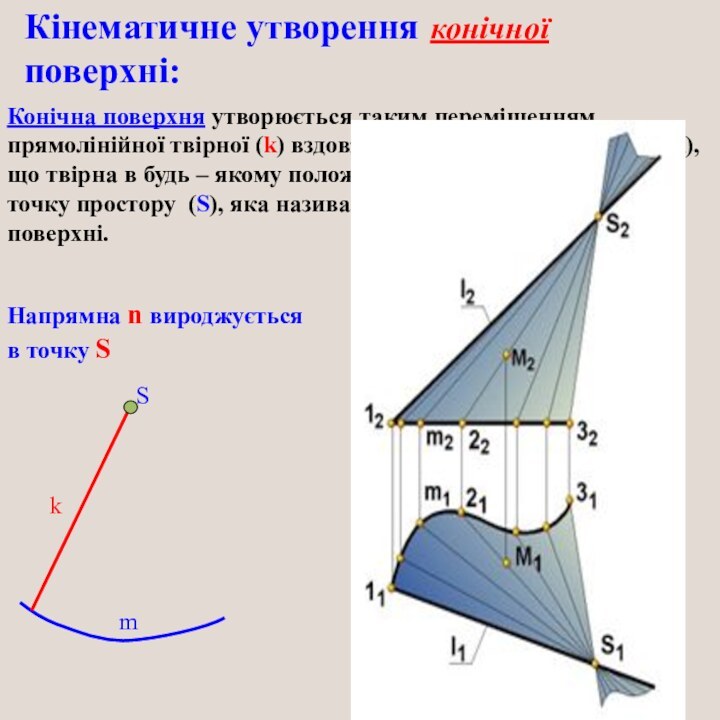
Кінематичне утворення конічної поверхні:
S
m
k
Конічна поверхня утворюється таким переміщенням
прямолінійної твірної (k) вздовж криволінійної напрямної (m), що твірна
в будь – якому положенні перетинає одну і ту саму точку простору (S), яка називається вершиною конічної поверхні.Напрямна n вироджується
в точку S
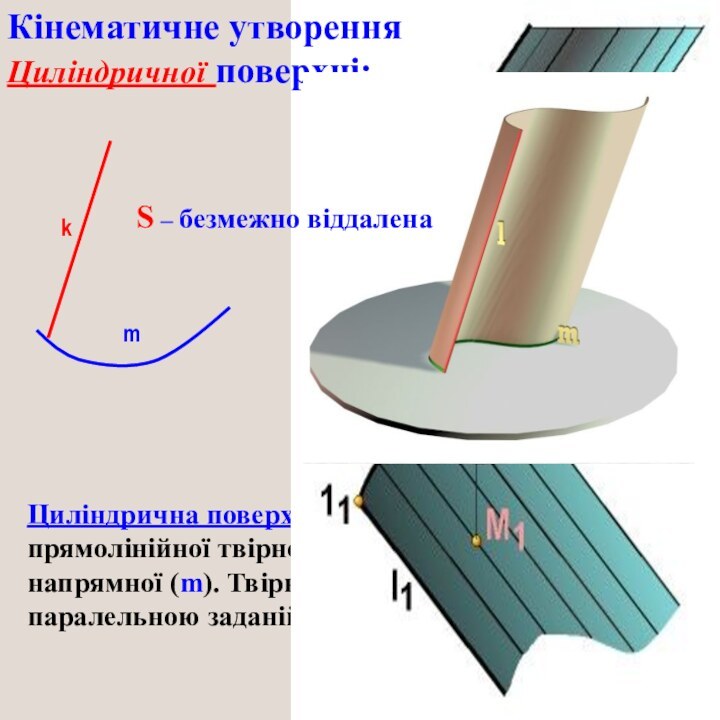
Слайд 12 Циліндрична поверхня утворюється переміщенням прямолінійної твірної (k) вздовж
криволінійної напрямної (m). Твірна весь час залишається паралельною заданій
прямій.m
k
Кінематичне утворення
Циліндричної поверхні:
S – безмежно віддалена
Слайд 13
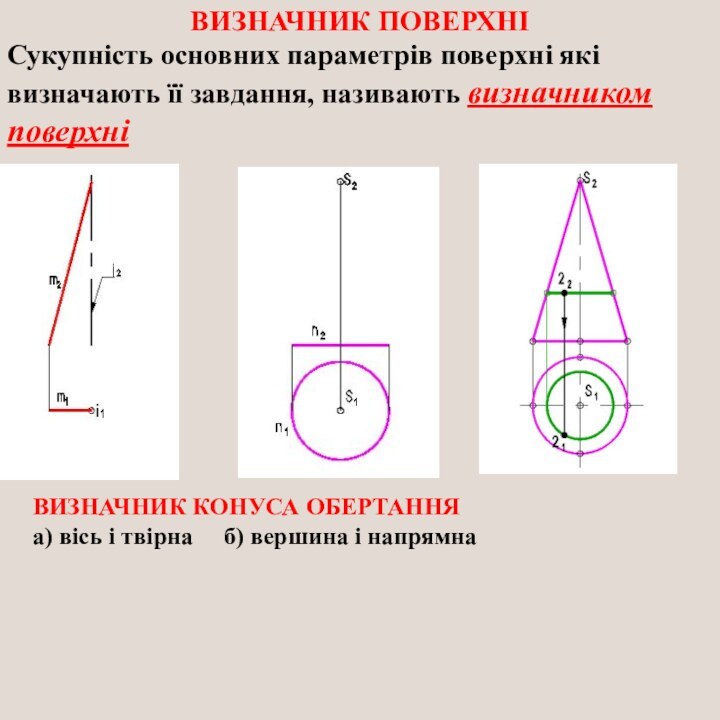
ВИЗНАЧНИК ПОВЕРХНІ
Сукупність основних параметрів поверхні які визначають її
завдання, називають визначником поверхні
ВИЗНАЧНИК КОНУСА ОБЕРТАННЯ
а)
вісь і твірна б) вершина і напрямна
Слайд 14
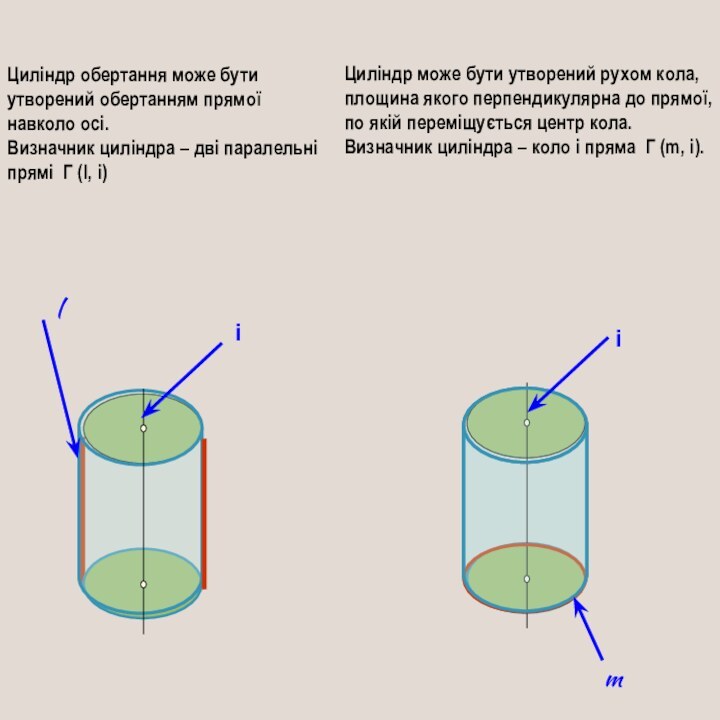
Циліндр обертання може бути утворений обертанням прямої навколо
осі.
Визначник циліндра – дві паралельні прямі Г (l,
i)Циліндр може бути утворений рухом кола, площина якого перпендикулярна до прямої, по якій переміщується центр кола.
Визначник циліндра – коло і пряма Г (m, i).
i
l
m
i
Слайд 15
За СПОСОБОМ УТВОРЕННЯ поверхні поділяються на такі класи:
Лінійчаті
поверхні загального виду, у тому числі гвинтові поверхні.
Поверхні обертання
лінійчаті і не лінійчаті. До них належать поверхні другого порядку. Поверхні другого порядку загального виду, тобто які отримані не обертанням.
Циклічні поверхні, які можуть бути утворені рухом кола сталого або змінного діаметра.
Незакономірні поверхні, що називаються також топографічними або такими, що задаються графічно, задаються за допомогою перерізів.
4. ОЗНАКИ КЛАСИФІКАЦІЇ КРИВИХ ПОВЕРХОНЬ
Слайд 16
5. РОЗГОРТНІ ЛІНІЙЧАТИ ПОВЕРХНІ
Лінійчатою називають поверхню, утворену рухом
прямої лінії. Такі поверхні поділяють на розгортні та
нерозгортні.
До розгортних відносять поверхні, які можна розгорнути на площину без розривів і складок. До них відносяться :
циліндрична поверхня;
конічна поверхня;
торсична поверхня.
Слайд 17
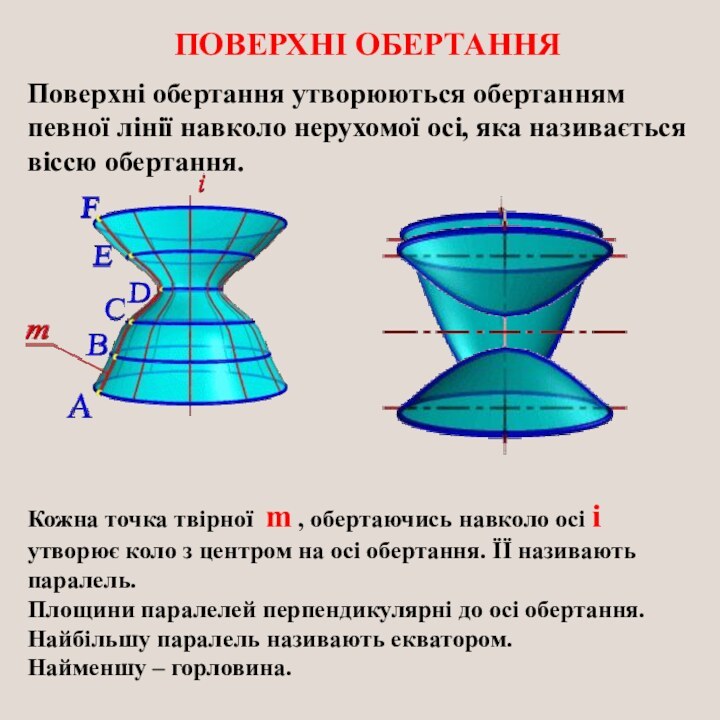
ПОВЕРХНІ ОБЕРТАННЯ
Поверхні обертання утворюються обертанням певної лінії навколо
нерухомої осі, яка називається віссю обертання.
Кожна точка твірної m
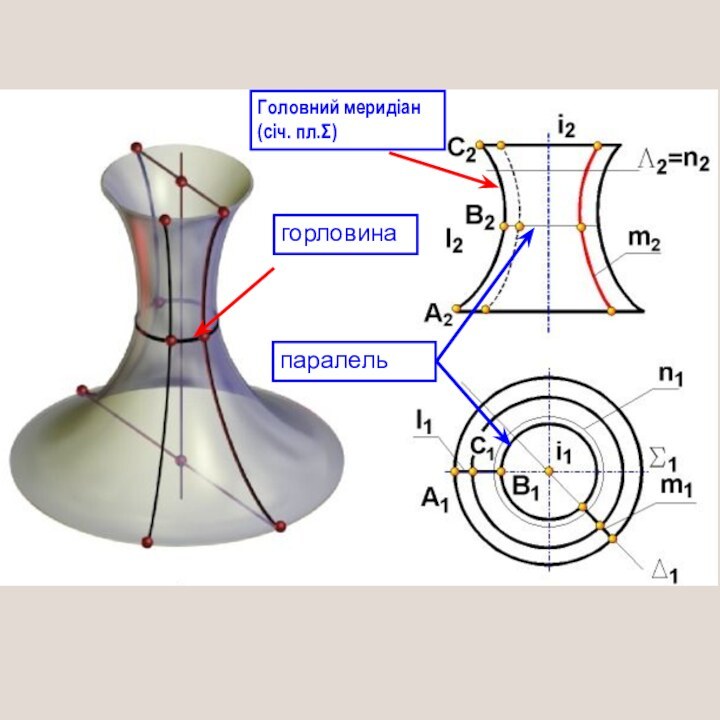
, обертаючись навколо осі i утворює коло з центром на осі обертання. ЇЇ називають паралель.Площини паралелей перпендикулярні до осі обертання.
Найбільшу паралель називають екватором.
Найменшу – горловина.
Слайд 19 СФЕРА - поверхня, яка утворюється обертанням кола навколо
своєї осі
m – твірна, гол. меридіан
i – вісь обертання
– горизонтально-проекцююча пряма n - екватор
Слайд 20 При обертанні кола (або її дуги) навколо осі,
яка належить до площини цього кола, але не проходить
через її центр, отримуємо поверхню з назвою ТОР:вісь
Слайд 21
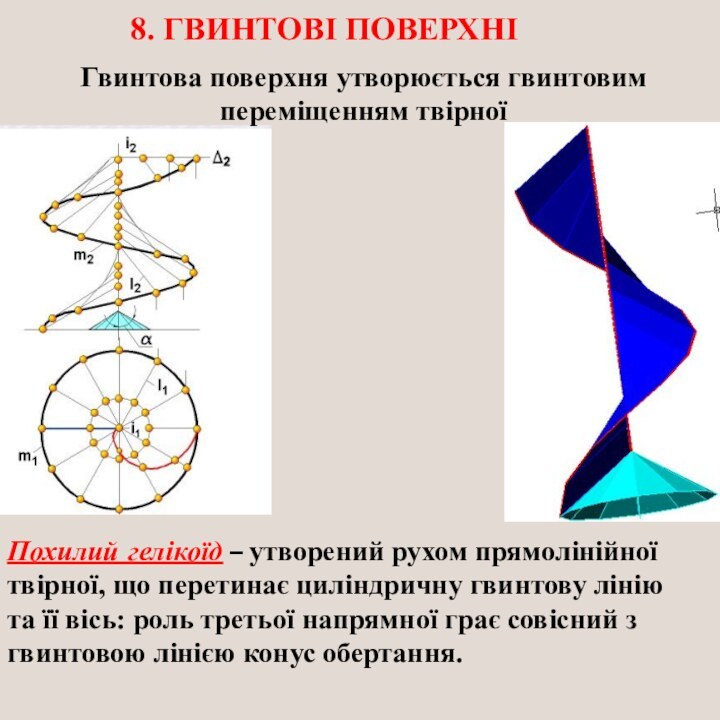
8. ГВИНТОВІ ПОВЕРХНІ
Похилий гелікоїд – утворений рухом прямолінійної
твірної, що перетинає циліндричну гвинтову лінію та її вісь:
роль третьої напрямної грає совісний з гвинтовою лінією конус обертання.Гвинтова поверхня утворюється гвинтовим переміщенням твірної
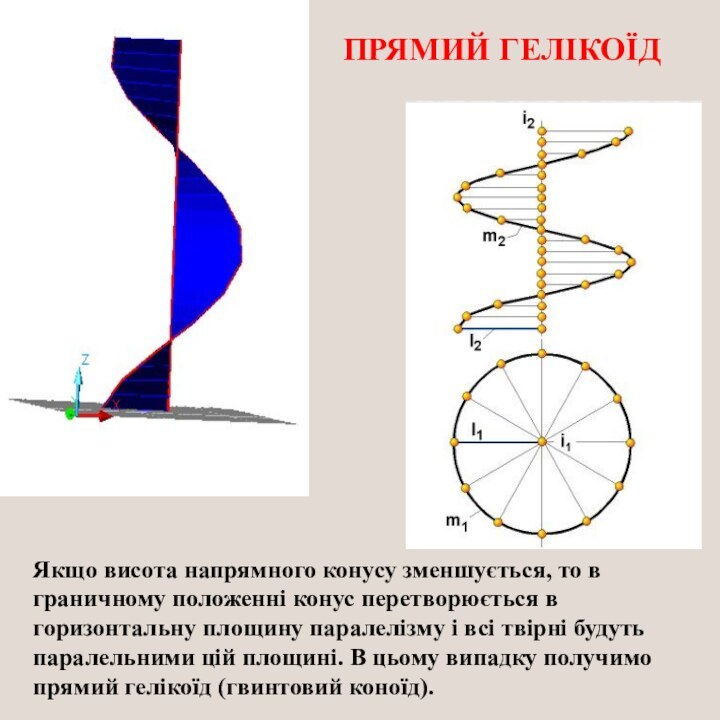
Слайд 22 Якщо висота напрямного конусу зменшується, то в граничному
положенні конус перетворюється в горизонтальну площину паралелізму і всі
твірні будуть паралельними цій площині. В цьому випадку получимо прямий гелікоїд (гвинтовий коноїд).ПРЯМИЙ ГЕЛІКОЇД
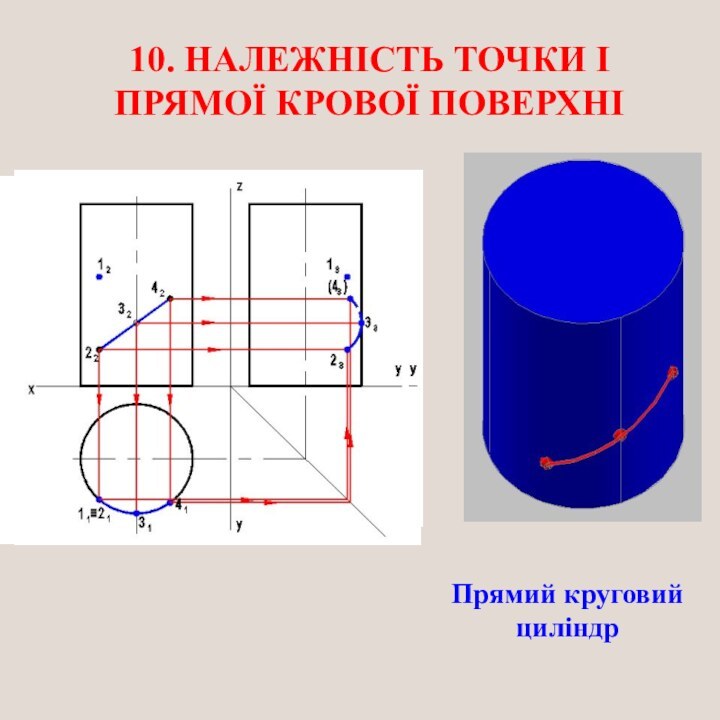
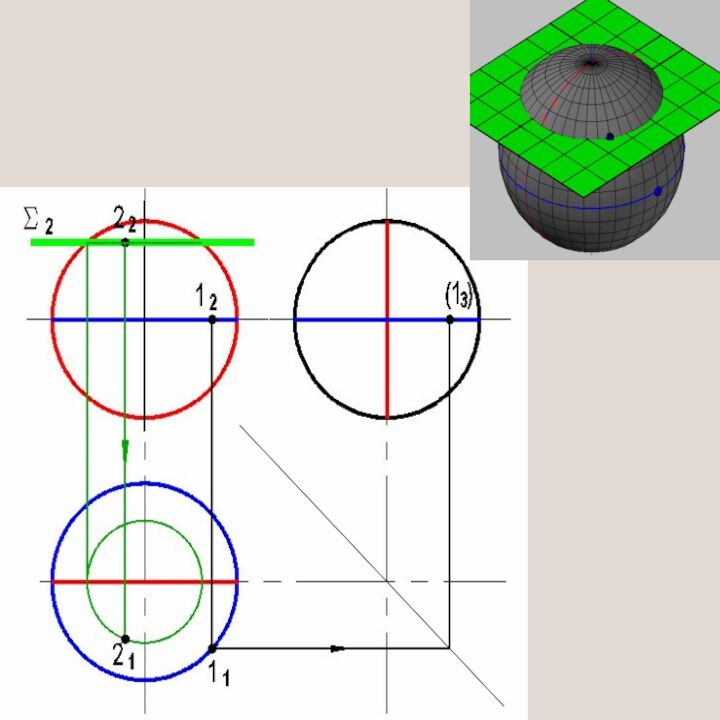
Слайд 26
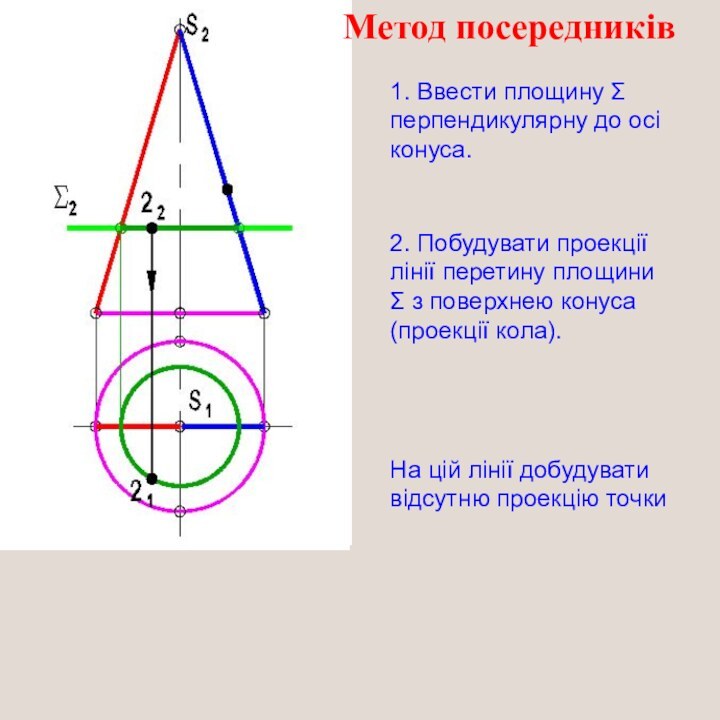
1. Ввести площину Σ перпендикулярну до осі конуса.
2.
Побудувати проекції лінії перетину площини Σ з поверхнею конуса
(проекції кола).На цій лінії добудувати відсутню проекцію точки
Метод посередників