Слайд 2
Введение
Актуальность темы. Участие в спортивных конкурсах позволяет пропагандировать

здоровый образ жизни среди учащихся школ. Интересные, интеллектуальные задания
спортивных состязаний повышают привлекательность конкурса. Использования топологии позволит сделать спортивные конкурсы более интеллектуальными, и, следовательно, более интересными.
Формулировка проблемы. Организация спортивных конкурсов всегда занимает много времени у организаторов. Надо продумать не только какими будут сами состязания, но и продумать и подготовить прочие организационные моменты: призы, последовательность прохождения командами разных состязаний и прочие моменты.
Разработанность исследуемой проблемы. Многочисленные поиски в сети интернет, в учебно-методических пособиях для школьных учителей физкультуры, общение с организаторами школьного спортивного конкурса в моей школе показали, что практически данной проблемой никто не занимался ввиду острой нехватки времени в школе у учителей физкультуры. Для них самое главное успеть организовать сам спортивный конкурс в самом стандартном исполнении.
Слайд 3
Мною была выдвинута гипотеза: топология проникает в различные
сферы нашей жизни, что дает возможность предположить, что она
является значимым разделом математики и экономики.
Цели исследования:
Что изучает топология, теория графов.
Исследовать возможность использования теории графов в организации спортивных конкурсов.
Слайд 4
Зарождение топологии
Топология является одним из самых «молодых» разделов
современной геометрии, занимающийся изучением свойств фигур, которые сохраняются при
сжатии, растяжении или изгибе. Топология появилась в конце 19 века.
Решение одной из топологических задач, предложено Эйлером – знаменитым математиком, положило формальное начало топологии как разделу математики.
Слайд 5
Термины в топологии
Основными терминами топологии являются граф и
узел. Граф – это схема, в которой объекты изображаются
с помощью точек, и соединяются между собой линиями.
Узел - условная точка, в которой соединяются кривые. Узлы бывают четные и нечетные. Четными называют узлы, в которых пересекаются четное число линий. Если в узле соприкасаются нечетное количество, то узел является – нечетным.
Слайд 6
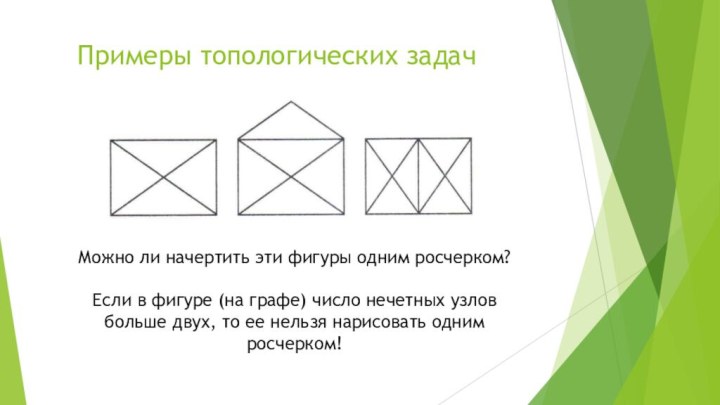
Примеры топологических задач
Можно ли начертить эти
фигуры одним росчерком?
Если в фигуре (на графе) число нечетных
узлов больше двух, то ее нельзя нарисовать одним росчерком!
Слайд 7
Теория графов в экономике
Теория графов используется
в экономике. Самым распространенным методом является метод «жадного алгоритма»
- достижение конечного результата с наименьшими затратами.
Теория графов в школьной экономике
Так же, теорию графов можно применить и в предстоящем капитальном или косметическом ремонте здании школы. Школьные кабинеты расположены в синем и оранжевом корпусах. Нанятая бригада рабочих, отделом по административному хозяйству, будет производить ремонтные работы в некоторых кабинетах обоих корпусов. Опираясь на мои знания, я могла бы помочь рабочим выполнить ремонт с минимальными физическими и временными затратами
Слайд 8
Задача о Кёнигсбергских мостах
Жители города Кёнигсберга, который был
расположен на берегах и двух островах реки Преголь и
соединены семью мостами, часто спорили о том, можно ли пройти через каждый мост по одному разу и вернуться в ту же точку, где начался путь.
Леонард Эйлер, великий математик, заинтересовавшись спором, помог жителям, решив эту задачу. Он доказал, что нельзя пройти через каждый мост по одному разу и вернуться в исходную точку согласно разработанной им теории графов.
Слайд 9
Решение Эйлера
Для решения задачи он заменил реальную картину
реки с мостами схемой, в которой два берега и
два участка суши изображены с помощью точек A,B,C,D, а мосты, соединяющие эти участки суши, изобразил с помощью линий a, b, c, d, e, f, g. Данная схема наглядно показывает, что в ней содержится более двух нечетных узлов, а именно, три: B, C, D.
Значит эту схему нельзя нарисовать одним росчерком и поэтому не существует такого пути, который позволил бы жителям города Кёнигсберга прогуляться по всем мостам только по одному разу и вернуться в исходную точку.
Слайд 11
Исследование возможности организации спортивного конкурса с использованием теории
графов
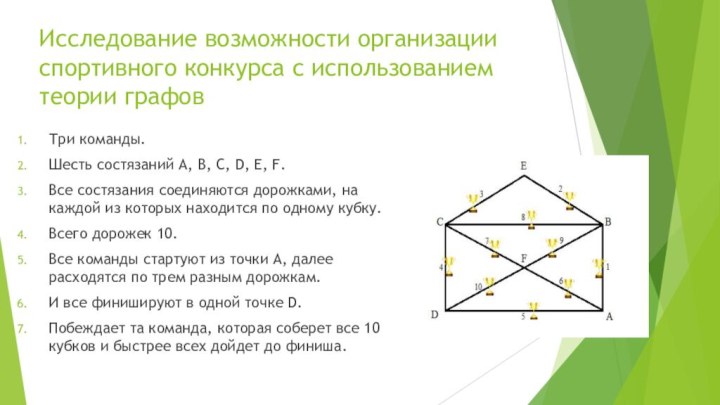
Три команды.
Шесть состязаний A, B, C, D, E, F.
Все состязания соединяются дорожками, на каждой из которых находится по одному кубку.
Всего дорожек 10.
Все команды стартуют из точки A, далее расходятся по трем разным дорожкам.
И все финишируют в одной точке D.
Побеждает та команда, которая соберет все 10 кубков и быстрее всех дойдет до финиша.
Слайд 12
Цель исследования
Исследовательская цель данного проекта заключалась в том,
чтобы найти ответы на вопросы:
1. Каким должен быть путь каждой
из трех команд, чтобы выполнить все требования спортивного конкурса?
2. Будут ли команды пересекаться на одной дорожке?
3. Есть ли вероятность того, что все три команды одновременно встретятся на одной дорожке?
Слайд 13
Решение исследовательской задачи
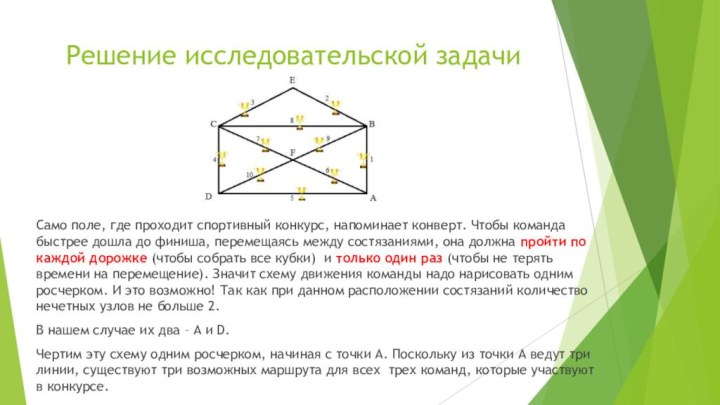
Само поле, где проходит спортивный конкурс,
напоминает конверт. Чтобы команда быстрее дошла до финиша, перемещаясь
между состязаниями, она должна пройти по каждой дорожке (чтобы собрать все кубки) и только один раз (чтобы не терять времени на перемещение). Значит схему движения команды надо нарисовать одним росчерком. И это возможно! Так как при данном расположении состязаний количество нечетных узлов не больше 2.
В нашем случае их два – A и D.
Чертим эту схему одним росчерком, начиная с точки A. Поскольку из точки A ведут три линии, существуют три возможных маршрута для всех трех команд, которые участвуют в конкурсе.
Слайд 14
Решение исследовательской задачи
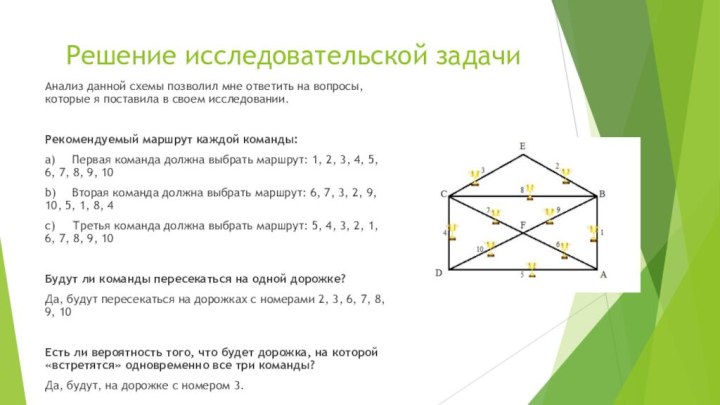
Анализ данной схемы позволил мне ответить
на вопросы, которые я поставила в своем исследовании.
Рекомендуемый
маршрут каждой команды:
a) Первая команда должна выбрать маршрут: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
b) Вторая команда должна выбрать маршрут: 6, 7, 3, 2, 9, 10, 5, 1, 8, 4
c) Третья команда должна выбрать маршрут: 5, 4, 3, 2, 1, 6, 7, 8, 9, 10
Будут ли команды пересекаться на одной дорожке?
Да, будут пересекаться на дорожках с номерами 2, 3, 6, 7, 8, 9, 10
Есть ли вероятность того, что будет дорожка, на которой «встретятся» одновременно все три команды?
Да, будут, на дорожке с номером 3.