- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Решение задач по многогранникам
Содержание
- 2. Повторить теоретический материал по теме «Многогранники». Применять знания при решении задач.
- 3. « Вдохновение в геометрии нужно не меньше,
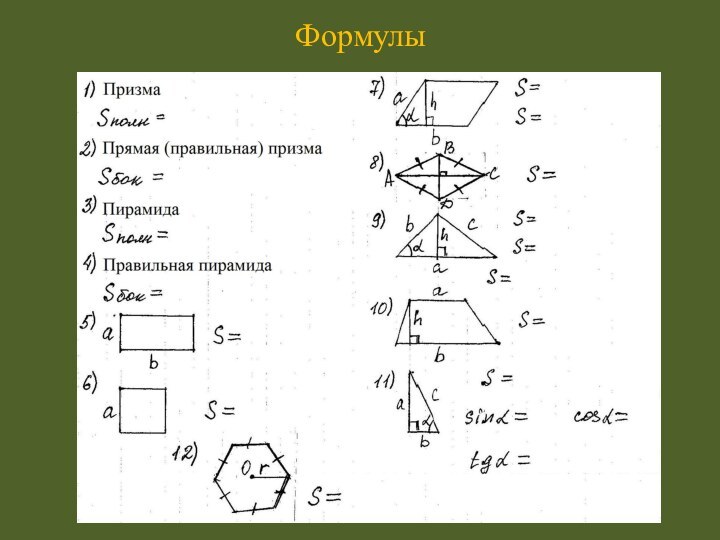
- 4. Формулы
- 5. Что называют многогранником?
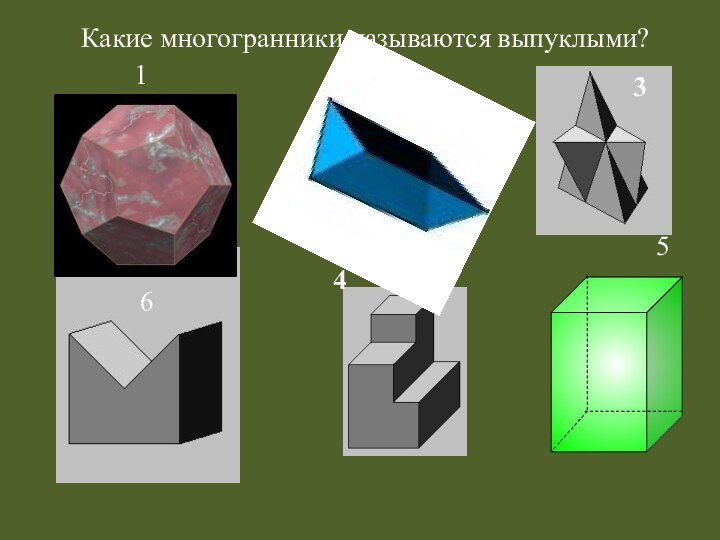
- 6. 123654Какие многогранники называются выпуклыми?
- 7. Многогранник, составленный из двух равных многоугольников
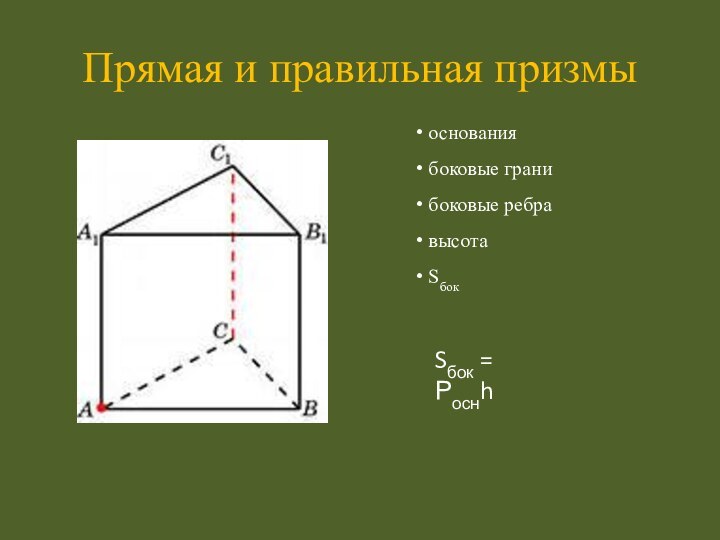
- 8. Прямая и правильная призмыSбок = Роснh основания
- 9. Правильные призмы
- 10. Многогранник, составленный из n-угольника А1А2…Аn и
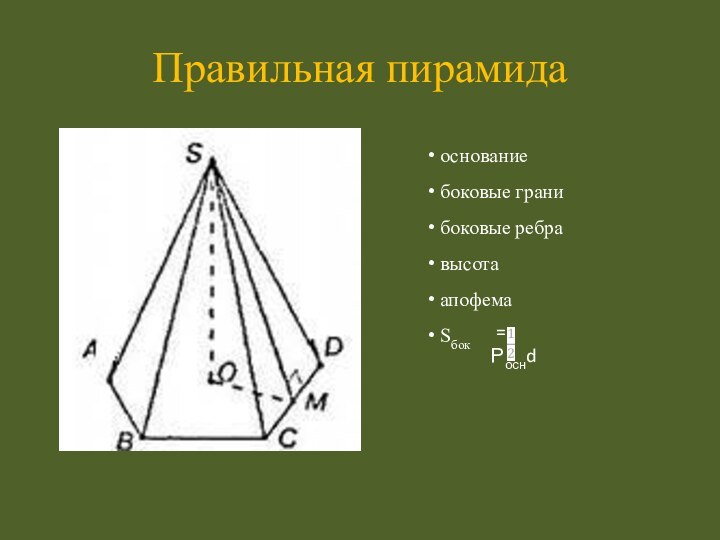
- 11. основание боковые грани боковые ребра высота апофема Sбок Правильная пирамида = Роснd
- 12. Платоновы тела Призма, в основании которой
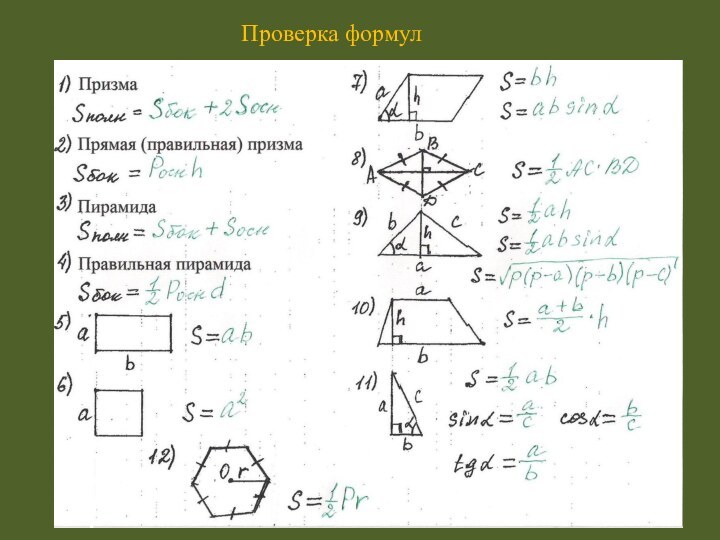
- 13. Проверка формул
- 15. Тест 1. Если точки М и N
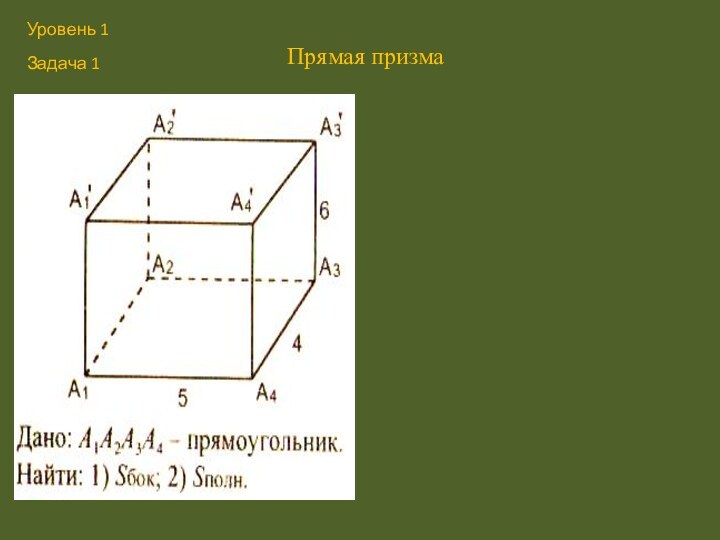
- 17. Прямая призмаУровень 1Задача 1
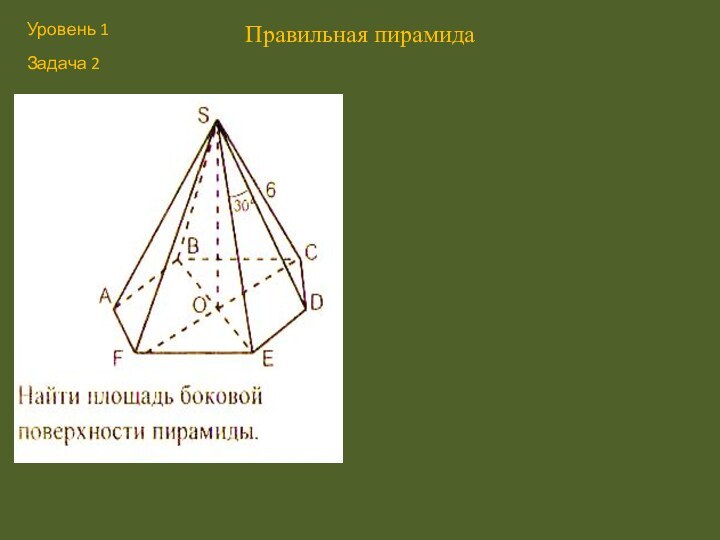
- 18. Правильная пирамида Уровень 1Задача 2
- 19. Демоверсия ЕГЭ,2013В9. Диагональ AC основания правильной четырёхугольной
- 20. Демоверсия ЕГЭ,2013С2. Сторона основания правильной треугольной призмы
- 21. В правильной четырехугольной пирамиде сторона
- 23. Домашнее задание Повторить теорию Задачи:
- 24. Скачать презентацию
- 25. Похожие презентации










Слайд 2
Повторить теоретический материал по теме «Многогранники».
Применять знания
при решении задач.
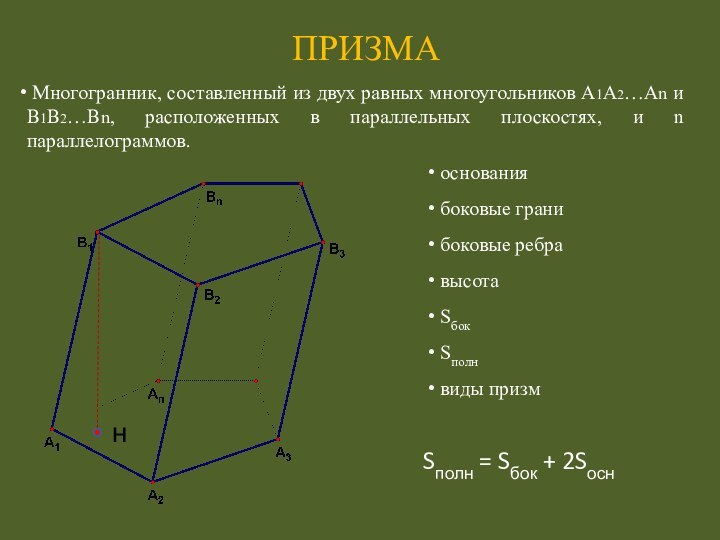
Слайд 7 Многогранник, составленный из двух равных многоугольников А1А2…Аn
и В1В2…Вn, расположенных в параллельных плоскостях, и n параллелограммов.
ПРИЗМА
н
Sполн
= Sбок + 2Sосн основания
боковые грани
боковые ребра
высота
Sбок
Sполн
виды призм
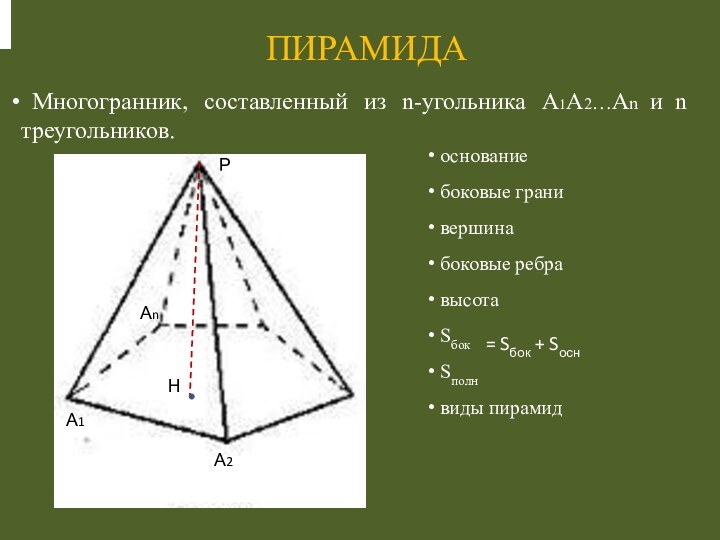
Слайд 10 Многогранник, составленный из n-угольника А1А2…Аn и n
треугольников.
ПИРАМИДА
А1
А2
Аn
Р
Н
= Sбок + Sосн
основание
боковые грани
вершина
боковые
ребравысота
Sбок
Sполн
виды пирамид
Слайд 12
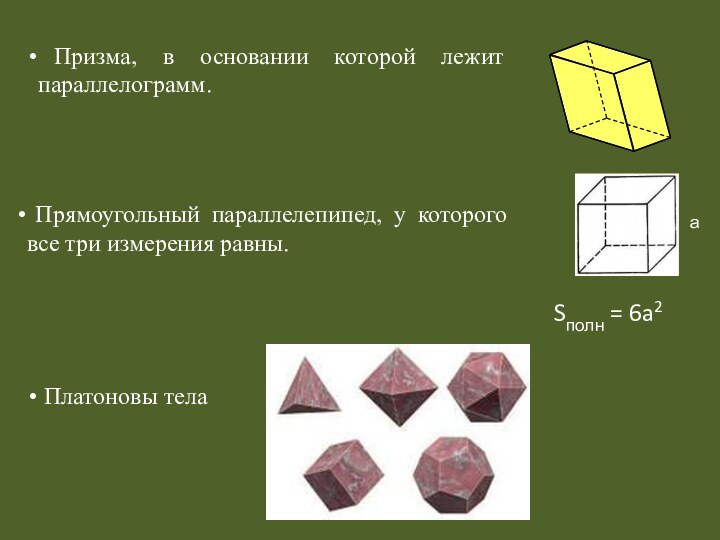
Платоновы тела
Призма, в основании которой лежит
параллелограмм.
Прямоугольный параллелепипед, у которого все три измерения равны.
а
Sполн
= 6a2
Слайд 15
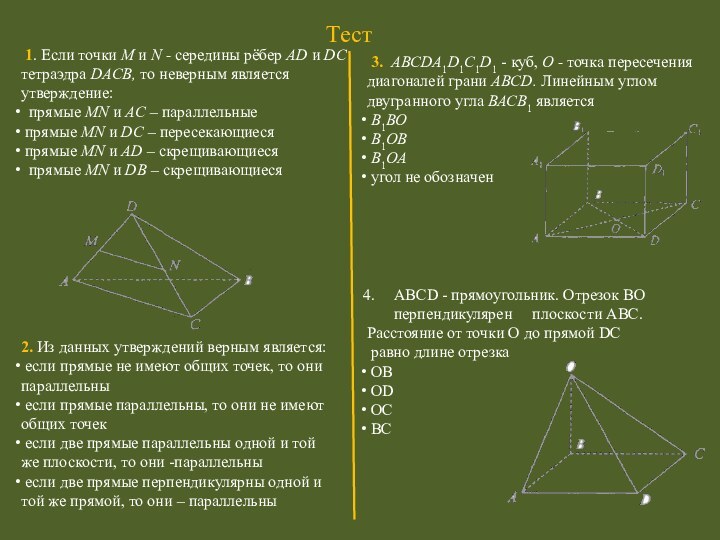
Тест
1. Если точки М и N -
середины рёбер AD и DC тетраэдра DACB, то неверным
является утверждение:прямые МN и AC – параллельные
прямые MN и DC – пересекающиеся
прямые MN и AD – скрещивающиеся
прямые MN и DB – скрещивающиеся
2. Из данных утверждений верным является:
если прямые не имеют общих точек, то они параллельны
если прямые параллельны, то они не имеют общих точек
если две прямые параллельны одной и той же плоскости, то они -параллельны
если две прямые перпендикулярны одной и той же прямой, то они – параллельны
3. ABCDA1D1C1D1 - куб, О - точка пересечения диагоналей грани ABCD. Линейным углом двугранного угла ВАСВ1 является
В1ВО
B1OB
В1ОА
угол не обозначен
ABCD - прямоугольник. Отрезок ВО перпендикулярен плоскости ABC.
Расстояние от точки О до прямой DC
равно длине отрезка
ОВ
OD
ОС
ВС
Слайд 19
Демоверсия ЕГЭ,2013
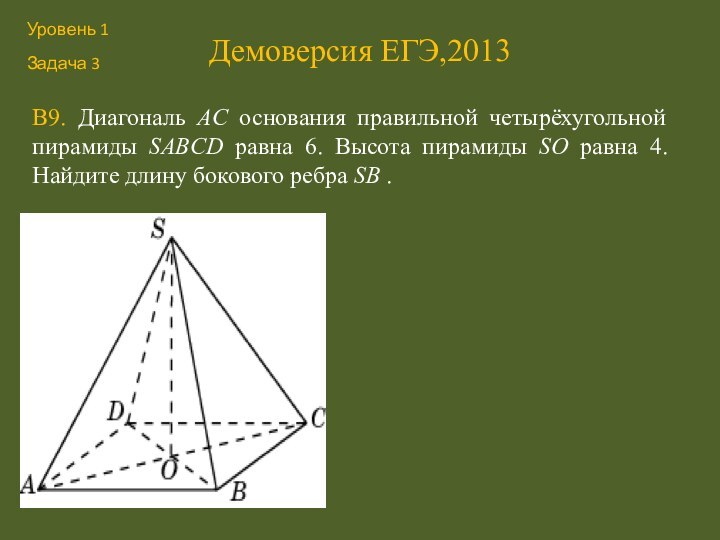
В9. Диагональ AC основания правильной четырёхугольной пирамиды
SABCD равна 6. Высота пирамиды SO равна 4. Найдите
длину бокового ребра SB .Уровень 1
Задача 3
Слайд 20
Демоверсия ЕГЭ,2013
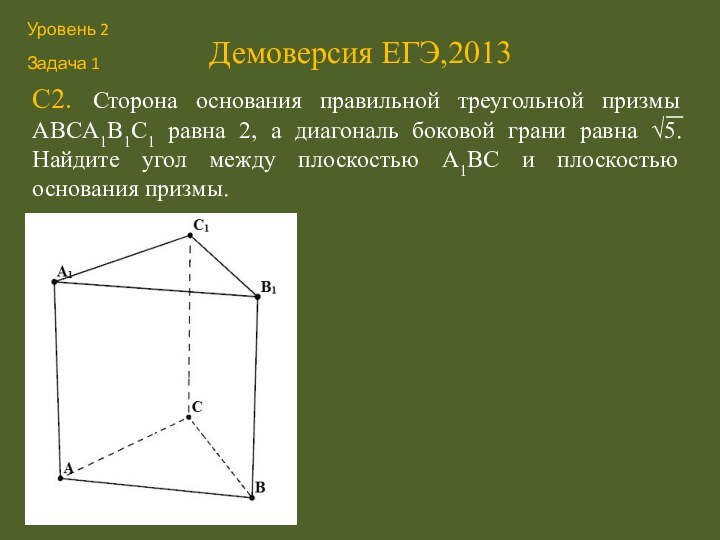
С2. Сторона основания правильной треугольной призмы ABCA1B1C1
равна 2, а диагональ боковой грани равна √5. Найдите
угол между плоскостью A1BC и плоскостью основания призмы.Уровень 2
Задача 1
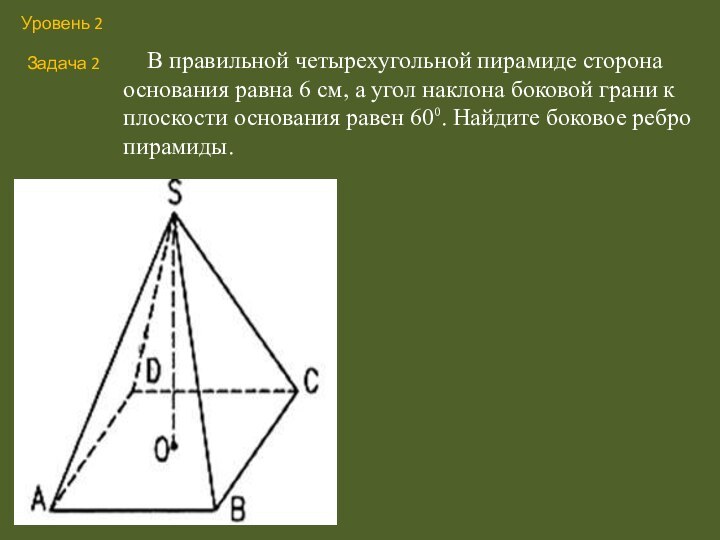
Слайд 21 В правильной четырехугольной пирамиде сторона основания
равна 6 см, а угол наклона боковой грани к
плоскости основания равен 60⁰. Найдите боковое ребро пирамиды.Уровень 2
Задача 2
Слайд 23
Домашнее задание
Повторить теорию
Задачи:
1уровень. Сторона основания правильной треугольной призмы равна 6
см, а диагональ боковой грани 10 см. Найдите площадь боковой и полной поверхности призмы.2уровень. DABC – пирамида, ∆ АВС – правильный, со стороной 6 см. DA ⊥ АВС, двугранный угол DBCA равен 30⁰. Найдите площадь боковой поверхности пирамиды.
Тесты http://geometry.far.ru/var1.php