- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Куля і cфера
Содержание
- 2. Ку́ля — це множина всіх точок простору,
- 4. Площу сфери, яка обмежує кулю з радіусом
- 5. Частини кулі: зеленим кольором позначено
- 6. Сегмент кулі — це та її частина,
- 7. Зріз — це стереометричне тіло, утворене перерізами
- 8. Сектор складається з кульового сегмента та конуса,
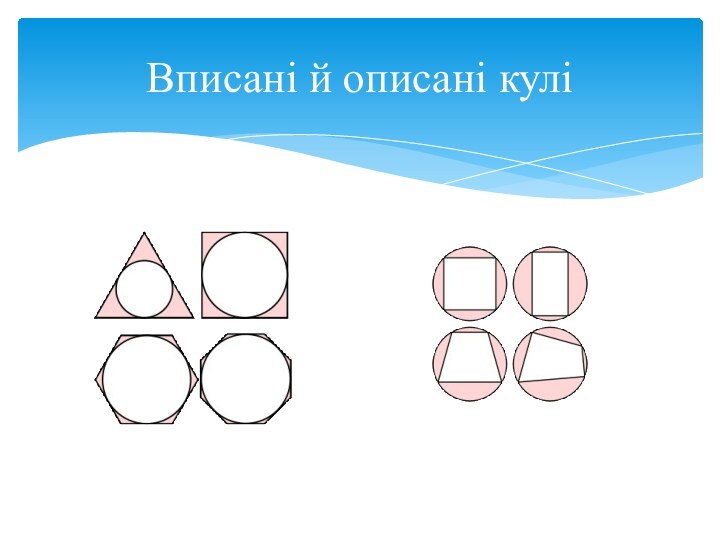
- 9. Вписані й описані кулі
- 10. Куля називається описаною навколо багатогранника, якщо всі
- 11. Куля називається вписаною в багатогранник, якщо всі
- 12. Куля так само, як циліндр і конус,
- 13. Сфе́ра (гр. σφαῖρα) - замкнута поверхня, геометричне
- 14. У аналітичній геометрії сфері з координатами
- 15. Сфера довільного радіусу з центром у початку
- 16. Скачать презентацию
- 17. Похожие презентации
Ку́ля — це множина всіх точок простору, що перебувають від заданої точки О на відстані, не більшій за дану відстань R. При цьому точка O називається центром, а R — радіусом кулі. Будь-який відрізок, який сполучає















Слайд 3
рівняння кулі з центром в точці з координатами (a,d,c) та радіусом R .
Взагалі, рівняння кулі у n-вимірному просторі виглядає як
де (a1,a2,….an) — координати її центра.
Куля в 2-вимірному просторі — круг, а в n-вимірному, якщо , вона називається гіперкулею.
Куля в аналітичній геометрії
Слайд 4 Площу сфери, яка обмежує кулю з радіусом R,
можна підрахувати за формулою :
, що приблизно дорівнює Площа поверхні кулі є найменшою серед площ поверхонь стереометричних тіл з однаковим об'ємом.
Об'єм кулі можна знайти за формулою :
Площа сфери та об'єм кулі
Слайд 5
Частини кулі:
зеленим кольором позначено сектор,
сірим — сегмент,
жовтим — зріз кулі.
Переріз кулі площиною
Слайд 6 Сегмент кулі — це та її частина, що
утворюється внаслідок перерізу площиною. Основними величинами, які характеризують сегмент,
є радіус кулі R та довжина перпендикуляра, опущеного на центр перерізу зі сфери , H . Довжина цього перпендикуляра також дорівнює різниці між радіусом R і відстанню від центра до перерізу l, тобто H=R - l.Таким чином об'єм сегмента дорівнює
а площа поверхні —
Сегмент кулі
Слайд 7 Зріз — це стереометричне тіло, утворене перерізами кулі
двома паралельними площинами.
Він характеризується такими величинами:
Радіус відповідної кулі,
R ;Відстань між двома перерізами, H ;
Радіуси обох перерізів, r1, r2 .
Об'єм зрізу визначається формулою :
Зріз
Слайд 8 Сектор складається з кульового сегмента та конуса, основа
якого збігається з основою сегмента, а вершина — з
центром кулі . Сектор характеризують радіус кулі R та довжина перпендикуляра, опущеного на центр основи конуса зі сфери, H .Об'єм сектора:
Площа його поверхні:
Сектор
Слайд 10
Куля називається описаною навколо багатогранника, якщо всі вершини
багатогранника лежать на поверхні кулі (сфери). В цьому випадку
багатогранник називають вписаним в кулю. Центр кулі, описаної навколо багатогранника, рівновіддалений від всіх його вершин, тобто є точкою перетину площин, проведених через середини ребер багатогранника (призми, піраміди) перпендикулярно до них. Відстань від центра кулі до вершин багатогранника — його радіус.Описана куля
Слайд 11 Куля називається вписаною в багатогранник, якщо всі грані
багатогранника дотикаються до кулі. Багатогранник у цьому випадку називається
описаним навколо кулі (сфери). Центр кулі, вписаної у багатогранник, рівновіддалений від усіх його граней. Він є точкою перетину півплощин, проведених через ребра двогранних кутів, утворених двома суміжними гранями, які поділяють цей кут навпіл. Відстань від центра кулі до граней — його радіус.Вписана куля
Слайд 12 Куля так само, як циліндр і конус, є
тілом обертання. Вона утворюється при обертанні півкруга навколо його
діаметра як осі. Цей діаметр називають віссю кулі, а його кінці — полюсами кулі.Відрізок, який сполучає дві точки кульової поверхні і проходить через центр кулі, називається діаметром. Кінці будь-якого діаметра називаються діаметрально протилежними точками кулі.
Додаткові відомості
Слайд 13
Сфе́ра (гр. σφαῖρα) - замкнута поверхня, геометричне місце
точок рівновіддалених від даної точки, що є центром сфери.
Сфера
Слайд 14 У аналітичній геометрії сфері з координатами
О(x0, y0, z0) і
радіусом r є геометричним місцем усіх точок (x, y, z), щоУ сферичній системі координат будь-яку точку сфери можна подати як:
Рівняння