различных значениях переменных x.
Например: x=2, x=5.
если x= 2, то
2x = 22 =4;если x= 5, то 2x = 25 =32;
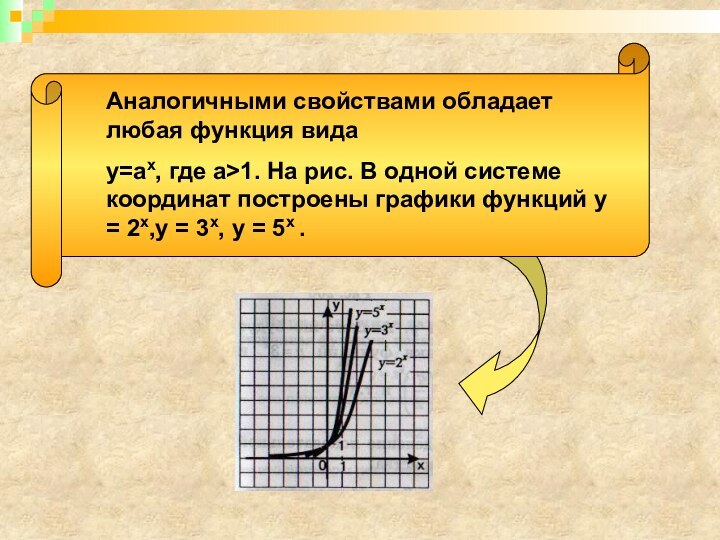
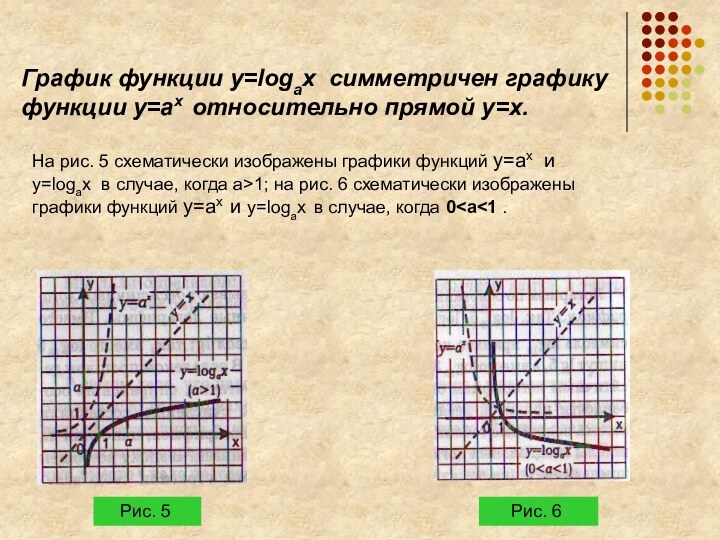
Поскольку у функции y= 2x аргумент x содержится в показателе степени, её называют показательной функцией.