- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Задачи на нахождение площади
Содержание
- 2. Вычисление площадей четырёхугольников является составной частью решения
- 3. Основная цельСформировать у учащихся понятие площади.Развить умение
- 4. СодержаниеУрок 1-й: «Площадь прямоугольника»Урок 2-й: «Площадь параллелограмма»Урок
- 5. «Площадь прямоугольника»Урок -объяснение нового материала, выполнен в
- 6. «Площадь параллелограмма»Урок -объяснение нового материала, выполнен в
- 7. «Площадь треугольника»Комбинированный урок , выполнен в виде
- 8. «Площадь трапеции»Урок- объяснение нового материала , выполнен
- 9. ПрОВЕРКА УСВОЕННОГО МАТЕРИАЛА Итоговые тесты по темам
- 10. Площадь трапецииУрок 4S
- 11. Вывести формулу площади трапеции показать её применение в процессе решения задач.Совершенствовать навыки в решении задачЦель урока:
- 12. Решить задачу Дано:ABCD-трапецияAD=12 см; BC=8см
- 13. Решение: трапеция ABCD состоит из 2 Δ:
- 14. Высота трапеции- перпендикуляр, проведённый из любой точки одного из оснований к прямой, содержащейдругое основаниеBH- высотаCH1,DH2,MN-высоты трапецииBCDMHAH2NH1
- 15. №480(а)Дано:ABCD-трапецияAB=21 см CD=17 см; BH=7см-высота
- 16. №482Дано:ABCD-трапецияAB=CD, B=135°KD=3,4 см; AK=1,4 см BK-высота
- 17. Скачать презентацию
- 18. Похожие презентации
Вычисление площадей четырёхугольников является составной частью решения задач по теме «Многоугольники» в курсе стереометрии, поэтому основное внимание уделяется формированию практических навыков вычисления площадей четырехугольников в входе решения задач. Также данный блок уроков важен при подготовке учащихся















Слайд 3
Основная цель
Сформировать у учащихся понятие площади.
Развить умение вычислять
площади фигур, применяя изученные свойства и формулы.
Расширить и углубить
представления об измерении площадей.Вывести формулы площадей прямоугольника, параллелограмма, трапеции, треугольника.
Слайд 4
Содержание
Урок 1-й: «Площадь прямоугольника»
Урок 2-й: «Площадь параллелограмма»
Урок 3-й:
«Площадь треугольника»
Урок 4-й: «Площадь трапеции»
Урок 5-й: «Проверка усвоенного материала»
Слайд 5
«Площадь прямоугольника»
Урок -объяснение нового материала, выполнен в виде
презентации «Power point».
В ходе урока учащиеся выводят площадь
прямоугольника и решают задачи по предложенной теме.
Слайд 6
«Площадь параллелограмма»
Урок -объяснение нового материала, выполнен в виде
презентации «Power point».
В ходе урока учащиеся выводят площадь
параллелограмма решают задачи и выполняют тест по изученной теме.
Слайд 7
«Площадь треугольника»
Комбинированный урок , выполнен в виде презентации
«Power point».
В ходе урока учащиеся выполняют самостоятельную работу
с самопроверкой по теме площадь параллелограмма с целью контроля усвоения изученного материала, выводят площадь треугольника и решают задачи по предложенной теме, проверяют полученные знания с помощью теста.
Слайд 8
«Площадь трапеции»
Урок- объяснение нового материала , выполнен в
виде презентации «Power point».
В ходе урока учащиеся выводят
площадь трапеции и решают задачи по изучаемой теме на закрепление материала.
Слайд 9
ПрОВЕРКА УСВОЕННОГО МАТЕРИАЛА
Итоговые тесты по темам площади выполнены
в двух вариантах в программе «Excel»
Вариант1 (теория)
Вариант 1 (практика)Вариант 2 (теория) Вариант 2 (практика)
Слайд 11 Вывести формулу площади трапеции показать её применение в
процессе решения задач.
Совершенствовать навыки в решении задач
Цель урока:
Слайд 12
Решить задачу
Дано:ABCD-трапеция
AD=12 см; BC=8см
AB=6 см A=30°
Найти:
S трапеции ABCDРешение:
SABCD= BK×(AD+BC)÷2
SABCD= 3×(12+8)÷2=60÷2=30(см²)
Слайд 13
Решение:
трапеция ABCD состоит из 2 Δ: ΔABD
и ΔBCD
Чтобы найти её площадь надо найти площади этих
треугольников.Проведём высоту BK в ΔABD
и DH в ΔBCD;
SABD=AD×BK÷2
SABCD= SABD+SBCD
SBCD=BC×DH÷2
SABCD= AD×BK÷2 +BC×DH÷2
= BK×(AD+BC)÷2
SABCD= BK×(AD+BC)÷2
BK- высота, AD,BC- основания
Теорема: Площадь трапеции равна произведению полусуммы её оснований на высоту
B
C
D
30º
8см
6см
K
A
H
Слайд 14
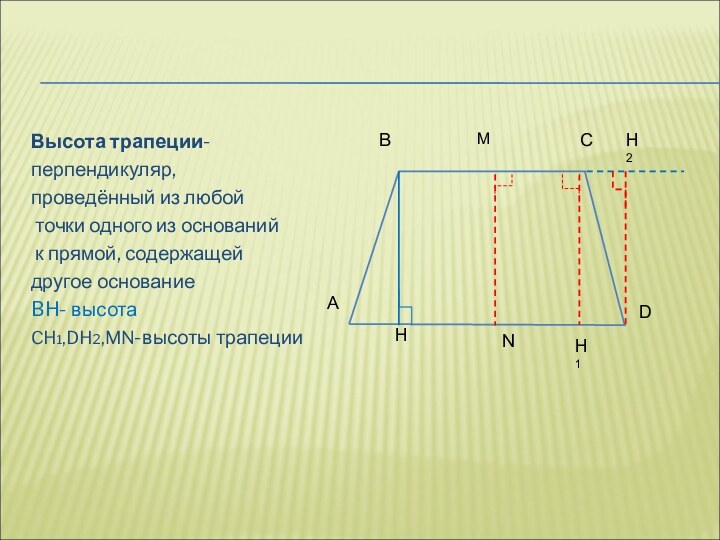
Высота трапеции-
перпендикуляр,
проведённый из любой
точки одного
из оснований
к прямой, содержащей
другое основание
BH- высота
CH1,DH2,MN-высоты трапеции
B
C
D
M
H
A
H2
N
H1
Слайд 15
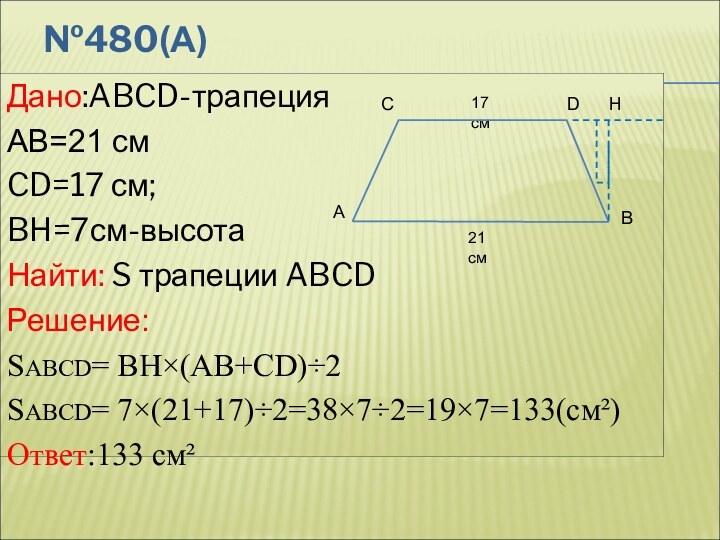
№480(а)
Дано:ABCD-трапеция
AB=21 см
CD=17 см;
BH=7см-высота
Найти: S трапеции
ABCDРешение:
SABCD= BH×(AB+CD)÷2
SABCD= 7×(21+17)÷2=38×7÷2=19×7=133(см²)
Ответ:133 см²
Слайд 16
№482
Дано:ABCD-трапеция
AB=CD, B=135°KD=3,4 см; AK=1,4 см
BK-высота
Найти: S трапеции
ABCDРешение:
1)в ΔABK K=90º ABK=135º- KBC=45º
A=90º- ABK=45º
2) Проведём высоту СE,
тогда KBCE-прямоугольник и BC=KE,а ΔDCE-прямоугольный, D=45º
3) ΔABK=ΔDCE по гипотенузе и острому углу(AB=CD, A= D)
DE=AK=1,4 см, значит KE=2см, BC=2см
4) AD=AK+KD=1,4+3,4=4,8см
SABCD= BK×(BC+AD)÷2
SABCD= 1,4×(2+4,8)÷2=4,76(см²)
Ответ:4,76см²
B
C
D
1,4 см
3,4 см
A
135°
К
E





























