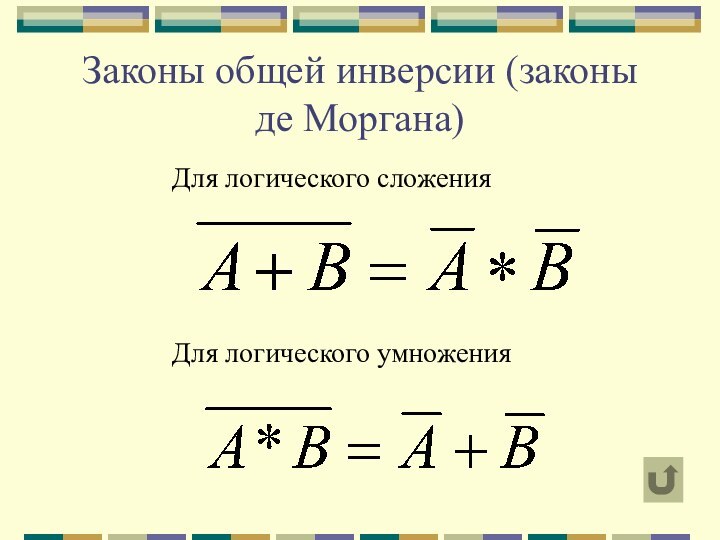
инверсии (законы де Моргана)
Закон коммутативности
Закон ассоциативности
Закон дистрибутивности
Закон идемпотентности (равносильности)
Законы
исключения константЗаконы поглощения
Законы исключения (склеивания)
Закон контрапозиции (правило перевертывания)
Выразить импликацию через конъюнкцию
Выразить эквивалентность через базовые логические операции