относительно которого исследователь хотел бы делать выводы в рамках
определённого исследованияПримеры ГС: все совершеннолетние жители Казани; все люди с заболеванием Альцгеймера
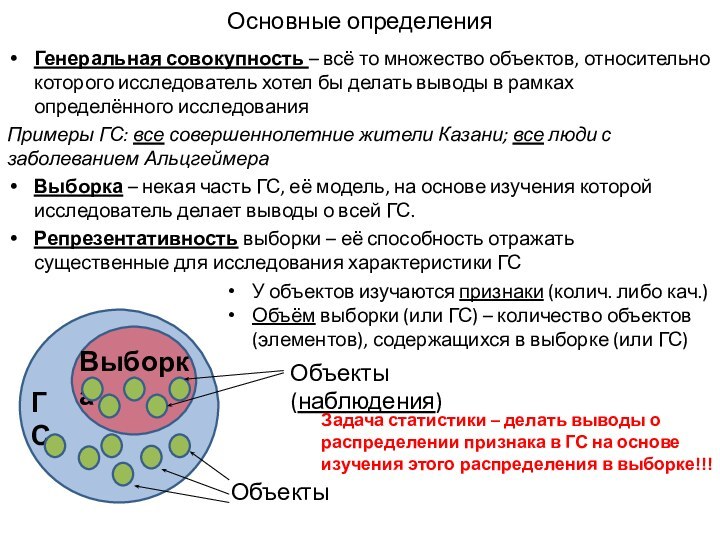
Выборка – некая часть ГС, её модель, на основе изучения которой исследователь делает выводы о всей ГС.
Репрезентативность выборки – её способность отражать существенные для исследования характеристики ГС
ГС
Выборка
Объекты
Объекты (наблюдения)
У объектов изучаются признаки (колич. либо кач.)
Объём выборки (или ГС) – количество объектов (элементов), содержащихся в выборке (или ГС)
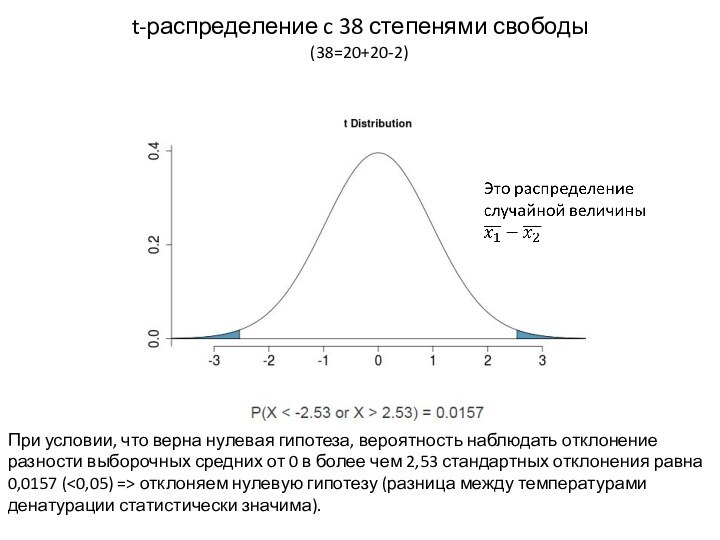
Задача статистики – делать выводы о распределении признака в ГС на основе изучения этого распределения в выборке!!!