- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Математические методы в педагогике
Содержание
- 2. Содержание 1. «Математические методы в педагогике».Тема №2 Обработка материалов педагогического исследования.Тема №3 Критерии теории вероятностей.Тема №4 Корреляционный анализ.
- 3. По мере развития педагогики и психологии в
- 4. Статистика - наука о массовых явлениях, с
- 5. Исходным понятием статистики является понятие «совокупность»- объединяющее
- 6. Члены совокупности могут сравниваться между собой в
- 7. Уместность применения того или иного статистического метода
- 8. это небольшая совокупность в статистике называется выборочной совокупностью (выборкой).
- 9. Главный принцип формирования выборки это случайный отбор
- 10. Генеральная совокупность составляют те учащиеся, на которых
- 12. также довольно сложно
- 13. Наиболее простой и часто применяемый вид эксперимента
- 14. Случайный отбор лучше производить по таблице случайных
- 15. Если требование случайности отбора строго выдержанно то
- 16. №2Обобщение
- 17. Измерение - приписывание
- 18. Измерение сделало естественные науки такими, какими
- 19. Категории, называемые числами, понятны любому
- 20. Измерительные шкалы Всего существует четыре типа шкал:
- 21. Числа в этих шкалах обладают разными свойствами:
- 22. Шкала наименований В этой шкале числа присвоенные объектам
- 23. Чисел в шкале наименований
- 24. Числа в шкале наименований
- 25. Шкала порядка (порядковая) Числа, присвоенные
- 26. ПродолжениеВ зависимости от желания исследователя большее число
- 27. Шкала порядка задается
- 28. Шкала интерваловВ отличие от двух предыдущих шкал
- 29. Однако, то, что
- 30. Шкала отношений В ней также существует единица
- 31. В этой шкале обязательно,
- 32. Между самими шкалами
- 33. Многомерные шкалыОни вводятся для установления связей с
- 34. Продолжение
- 35. Статистическая группировка, которая представляет собой простую группировку
- 36. Признаки – характеристики изучаемого объекта, формируются при
- 37. упорядочивание в ранжированном ряду; составление списка характеристик
- 38. Для них вычисляется процентная величина ni/n*100%,где n
- 39. Пример Группировка по номинальному признаку. Например n=600 респондентов:
- 40. Таблица 1 . Распределение респондентов по уровню образования
- 41. Полигон распределения
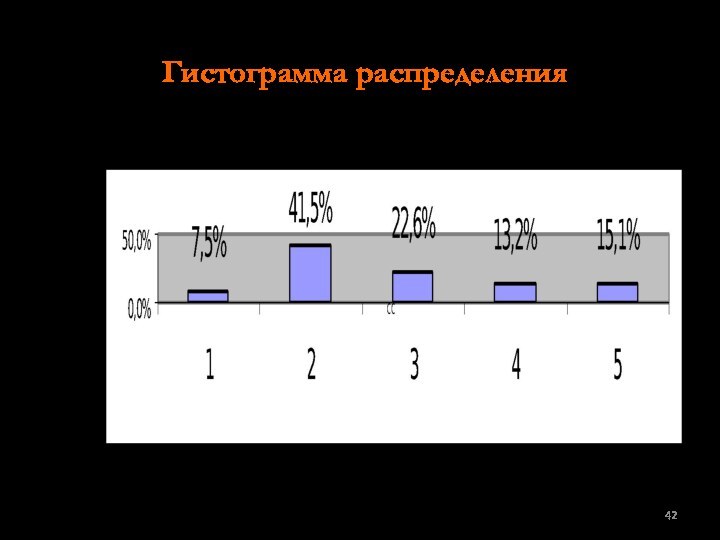
- 42. Гистограмма распределения
- 43. Мода Числовой характеристикой выборки, как правило, не
- 44. Так, например, в ряду значений (2, 6,
- 45. Моду находят согласно следующим правилам: В том случае,
- 46. Когда два соседних (смежных) значения имеют одинаковую
- 47. Если два несмежных (не соседних) значения в
- 48. Могут существовать и так называемые мультимодальные распределения,
- 49. Медиана Медиана — обозначается X (X с волной
- 50. Пример 1 Найдем медиану выборки:9, 3,
- 51. Пример 2. Найдем медиану выборки: 20, 9,
- 52. Среднее арифметическое Среднее арифметическое ряда из п числовых
- 53. Здесь величины 1, 2... являются так называемыми
- 54. Знак является символом операции
- 55. Дисперсия Рассмотрим еще одну очень важную числовую характеристику
- 56. где п — объем выборкиi - индекс суммирования- среднее арифметическое
- 57. Пример 3. Вычислим дисперсию следующего ряда 2,
- 58. Так образуется новый ряд чисел. Его особенность
- 59. Определение процентилейРаспределение частот дает полезную для психологов
- 60. Поэтому исследователей наряду с абсолютными величинами характеристик
- 61. Пример 4. Для данных опроса студентов получим:
- 62. Пример нахождения среднее квадратичного отклонения результатов
- 64. Асимметрия. Это мера ''косости'' или ''скошенности'' распределения. Распределения,
- 65. В тех случаях, когда количество значений больших
- 66. В симметричном распределении асимметрия точно равна нулю,
- 67. Эксцесс Это мера ''выпуклости'' или ''крутости'' распределения. При
- 68. Эксцесс служит для того, чтобы определить крутизну
- 69. Эксцесс рассчитывается по формуле: Особенностью всех мер
- 70. Пример расчет меры центральной тенденции, параметров и мер рассеивания
- 72. Расчет мер центральной тенденции и параметров распределения:, , , ,
- 74. Относительно данного распределения можно сказать, что: распределение
- 75. Оно характеризуется положительной асимметрией, что означает, что
- 76. Необходимо сказать, что рассчитанные в этом примере
- 77. Тема №3 Критерии теории вероятностей Критерий Фишера Критерий
- 78. где - дисперсии первой и второй
- 79. Так как, согласно условию критерия, величина числителя
- 80. В таблице критических значений критерия Фишера находятся
- 81. Пример В двух третьих классах проводилось тестирование
- 82. Решение. Необходимо сравнить дисперсии тестовых оценок в обоих классах. Результаты тестирования представлены в таблице:
- 83. Рассчитав дисперсии для переменных X и Y,
- 84. По таблице из приложения для F критерия
- 85. Фи - критерий Фишера с угловым преобразованием
- 86. где – угол, соответствующей большей процентной доле,
- 87. Он имеет следующие особенности: Позволяет сравнивать две выборки
- 88. Позволяет сопоставить выборки как по качественному, так
- 90. Вывод: группы испытуемых не различаются достоверно по проявлению эффекта, т.к.
- 91. Перечисленные выше статистические критерии предназначены только для
- 92. Многие ответы на вопросы могут быть получены
- 93. Критерий Н-Крускала-Уоллиса Критерий Н применяется для оценки различий
- 94. Критерий основан на том принципе, что чем
- 95. Работа с данными начинается с того, что
- 96. Критерий построен на следующей идее – если
- 97. Пример. Четыре группы испытуемых выполняли тест Бурдона в
- 98. Решение. Число ошибок показателя переключаемое внимания в процентах дано в таблицеТаблица 1
- 99. Для дальнейшей работы с критерием необходимо выстроить
- 100. Таблица 2
- 101. Таблица 3
- 102. Где N – общее число членов в
- 103. При определении критических значений критерия применительно к
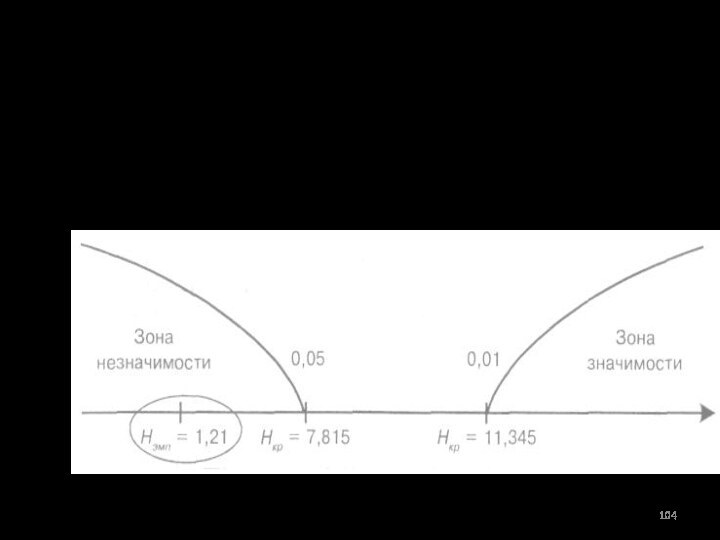
- 104. Соответствующая “ось значимости” имеет вид:
- 105. Переформулируем полученный результат в терминах нулевой и
- 106. Иными словами, различные условия проведения теста Бурдона
- 107. Для использование критерия Н необходимо соблюдать следующие
- 108. 5. Таблица критериев только для трех выборок,
- 109. – критерий Вилкоксона. Этот критерий применяется для решения
- 110. T = 3 + 3 + 5,5 + 7,5 = 19Вывод: влияние фактора достоверно, т.к.
- 111. Тема №4 Корреляционный анализ. Взаимосвязи на языке
- 112. Рис. 1
- 113. Если увеличение одной переменной связано с увеличением
- 114. Функциональные связи, подобные изображенным на рис.1, являются
- 115. Однако даже в физических экспериментах эмпирическая взаимосвязь
- 116. Особенности коэффициента корреляции Коэффициент корреляции показывает сразу два
- 117. Коэффициент корреляции всегда находится в пределах от
- 118. При коэффициенте корреляции равном нулю признается отсутствие
- 119. если речь идет о положительной связи, и
- 120. По этой причине в реальных условиях почти
- 121. Причина этого заключается в том, что связь
- 122. Что касается психологических измерений, то здесь коэффициент
- 123. то тест может быть признан надежным, несмотря
- 124. Коэффициент корреляции « » При сравнении
- 125. ПРИМЕР Влияет ли семейное положение на успешность
- 126. Таблица 1
- 127. где рх – частота или доля признака,
- 128. Частоты вычисляется следующим образом: подсчитывается количество 1
- 129. Пусть рх соответствует доли студентов, имеющих 1
- 130. Подсчитаем рху – долю студентов, имеющих единицу
- 131. Число степеней свободы в нашем случае будет
- 132. Иными словами, психолог не обнаружил никакой связи
- 133. ЛИТЕРАТУРА Основная:Сидоренко Е.В. Методы математической обработки в
- 134. Дополнительная: Шевандрин Н.И. Психодиагностика, коррекция и развитие
- 135. Скачать презентацию
- 136. Похожие презентации
Содержание 1. «Математические методы в педагогике».Тема №2 Обработка материалов педагогического исследования.Тема №3 Критерии теории вероятностей.Тема №4 Корреляционный анализ.





































































































































Слайд 2
Содержание
1. «Математические методы в педагогике».
Тема №2
Обработка материалов
педагогического исследования.
Слайд 3 По мере развития педагогики и психологии в них
все больше начинают применятся математические, статистические методы и ЭВМ.
От педагога – исследователя требуется сейчас хорошие знания информатики, основ математических и статистических методов, а также умения ставить и решать исследовательские задачи с помощью ЭВМ.
Слайд 4 Статистика - наука о массовых явлениях, с помощью
которых можно получить обобщенные данные об изучаемых совокупностях, рассчитать
показатели, связи и явления, обнаружить закономерности развития изучаемых процессов.Слайд 5 Исходным понятием статистики является понятие «совокупность»- объединяющее множество
испытуемых (учащихся) по одному или нескольким интересующим нас признакам.
Главное требование к выделению изучаемой совокупности это ее качественная однородность, например по уровню знаний, росту, весу и др. признакам.
Слайд 6 Члены совокупности могут сравниваться между собой в отношении
того качества, которое является основным предметом исследования при этом
абстрагируется от других не интересующих нас качеств например если педагог или психолог исследуют успеваемость учащихся, то он естественно не принимает во внимание их рост, вес или другие параметры, не относятся непосредственно к изучаемому вопросу.Слайд 7 Уместность применения того или иного статистического метода зависит
от способа образования исследуемой совокупности и от количества испытуемых,
применения большинства математических методов основано на идеи использования небольшой случайной совокупности испытуемых из общего числа тех, на которых могли были бы распространить выводы полученные в результате изучения совокупности-Слайд 9 Главный принцип формирования выборки это случайный отбор испытуемых
из мыслимого множества учащихся называемого генеральной совокупностью. По анализу
элементов содержащихся в капле крови медики не редко судят о составе всей крови человека, так и по выборочной совокупности учащихся изучаются явления характерные для всей генеральной совокупности.Слайд 10 Генеральная совокупность составляют те учащиеся, на которых можно
распространить выводы, полученные на выборке.
Школьный класс, на
который проводится большинство педагогических и психологических экспериментов не является, строго говоря, выборочной совокупностью.Слайд 11 Специфической
особенностью педагогических экспериментов является то, что в них почти
никогда не выдерживается требование случайности отбора по вполне понятной причине: учащиеся занимающиеся в классе и в процессе учебы трудно отбирать в случайном порядке,Слайд 12 также довольно сложно отбирать
учеников из разных классов и разных школ и формировать
из них экспериментальную и контрольную группы.Это обстоятельство дает некоторые основания относить эксперименты, проводимые в школьных классах к числу так называемых КВАЗИ – экспериментов.
Слайд 13 Наиболее простой и часто применяемый вид эксперимента –
это исследование экспериментальная и контрольная группа. Из числа членов
генеральной совокупности в случайном порядке формируется 2 группы учащихся.Слайд 14 Случайный отбор лучше производить по таблице случайных чисел
или классически другим методам обеспечивающий равный шанс каждому попасть
в выборочную совокупность. Так же в случайном порядке отобранные учащиеся разбиваются на экспериментальные и контрольные группы.Слайд 15 Если требование случайности отбора строго выдержанно то обе
группы оказываются примерно одинаковыми по уровню начальной подготовленности и
по другим признакам, влияющим на усвоение предмета.
Слайд 16
№2
Обобщение первичной информации
с привлечением математических приемов.
А)Измерение и измерительные шкалы
Слайд 17 Измерение - приписывание
чисел объектам или явлениям в соответствии с определенными правилами.
Измерение является опытной или экспериментальной процедурой, результатом активного взаимодействия исследователя с объектом познания. Переход от описания объекта познания к его измерению всегда означал переход к точному знанию
Слайд 18 Измерение сделало естественные науки такими, какими они
существуют сегодня.
А проникновение измерительных
процедур в гуманитарные области знания приближает их к точным наукам. Слайд 19 Категории, называемые числами, понятны любому взрослому
человеку и любая измерительная процедура, в конечном счете, обязательно
должна закончиться числом.Однако, число, приписанное объекту, еще ни о чем не говорит, если не известны правила, по которым происходило это приписывание. Число приобретает смысл только в том случае, если известна шкала, в которой происходило измерение.
Слайд 20
Измерительные шкалы
Всего существует четыре типа шкал: шкала
наименований (номинальная шкала), шкала порядка (порядковая или ординальная шкала),
шкала интервалов и шкала отношений (абсолютная или пропорциональная шкала).Слайд 21 Числа в этих шкалах обладают разными свойствами: они
могут говорить о степени выраженности измеряемого признака, о количественных
различиях между объектами и т.д.В зависимости от типа шкалы к числам могут быть применимы, а могут быть и неприменимы те или иные математические операции.
Слайд 22
Шкала наименований
В этой шкале числа присвоенные объектам говорят
только лишь о том, что эти объекты различаются.
По
сути, это классификационная шкала. Так, например, исследователь может приписать женщинам ноль, а мужчинам единицу, или наоборот, и это будет говорить только о том, что это два разных класса объектов.Слайд 23 Чисел в шкале наименований может
быть столько, сколько существует классов объектов подлежащих измерению, но
ни сумма этих чисел, ни их разность, ни произведение не будут иметь никакого смысла, т.к. в шкале наименований не осуществима ни одна арифметическая операция.Слайд 24 Числа в шкале наименований могут
быть любыми, хотя, как правило, отрицательные не используются. Наиболее
часто в психологических исследованиях используется дихотомическая шкала наименований, которая задается двумя числами – нулем и единицей
Слайд 25
Шкала порядка (порядковая)
Числа, присвоенные объектам
в этой шкале, будут говорить о степени выраженности измеряемого
свойства у этих объектов, но, при этом, равные разности чисел не будут означать равных разностей в количествах измеряемых свойств.
Слайд 26
Продолжение
В зависимости от желания исследователя большее число может
означать большую степень выраженности измеряемого свойства или меньшую, но
в любом случае, между числами и соответствующими им объектами сохраняется отношение порядка.Слайд 27 Шкала порядка задается положительными
числами, и чисел в этой шкале может быть столько,
сколько существует измеряемых объектов.Примеры шкал порядка: рейтинг испытуемых по какому-либо признаку, результаты экспертной оценки испытуемых и т.д.
Слайд 28
Шкала интервалов
В отличие от двух предыдущих шкал в
этой шкале существует единица измерения, либо реальная (физическая), либо
условная, при помощи которой можно установить количественные различия между объектами в отношении измеряемого свойства.Равные разности чисел в этой шкале будут означать равные различия в количествах измеряемого свойства у разных объектов, или у одного и того же объекта в разные моменты времени
Слайд 29 Однако, то, что одно
число оказывается в несколько раз больше другого, не обязательно
говорит о таких же отношениях в количествах измеряемых свойств.В шкале интервалов может быть задействована вся числовая ось, но при этом ноль не указывает на отсутствие измеряемого свойства, т.к. нулевая точка часто является произвольной, как в шкале температуры по Цельсию, либо вообще отсутствует, как в некоторых шкалах психологических тестов.
Слайд 30
Шкала отношений
В ней также существует единица измерения,
при помощи которой объекты можно упорядочить в отношении измеряемого
свойства и установить количественные различия между ними.Особенностью шкалы отношений является то, что к числам в этой шкале применимы все математические операции.
Слайд 31 В этой шкале обязательно, по,
крайней мере, теоретически, присутствует ноль, который говорит об абсолютном
отсутствии измеряемого свойства. В психологии из шкал отношений наиболее часто используются шкала вероятностей и шкала ''сырых'' баллов (количество решенных заданий, количество ошибок, количество положительных ответов и т.д.).Слайд 32 Между самими шкалами тоже
существуют отношения порядка. Каждая из перечисленных шкал является шкалой
более высокого порядка по отношению к предыдущей шкале.Так, например, измерения, произведенные в шкале отношений можно перевести в шкалу интервалов, из шкалы интервалов – в шкалу порядка и т.д., но обратная процедура будет невозможна
Слайд 33
Многомерные шкалы
Они вводятся для установления связей с разных
сторон:
Очень большой познавательный интерес- очень слабый интерес. Между ними:
большой интерес, средний, слабый.К многомерным шкалам иногда относя и биполярную шкалу с нулевой величиной в центре.
Слайд 34
Продолжение
Имя
Ф. Дисциплинированность
НедисциплинированностьАккуратность Неаккуратность
Ярко выраженное 5 4 3 2 1 0 1 2 3 4 5 Неярко выраженное
свойство свойство
По оценочным шкалам могут быть построены графики
Слайд 35 Статистическая группировка, которая представляет собой простую группировку респондентов
(то есть опрошенных лиц) с учетом социально-демографических данных (пол,
возраст, род занятий и т.п.) признаков. Позволяет суммировать число ответов на вопросы анкеты, сопоставлять и сравнивать по признакам.Статистическая группировка
Слайд 36 Признаки – характеристики изучаемого объекта, формируются при построении
гипотез в начале разработки исследования.
Группировка (объединение) характеристик происходит
на основании типа шкалы измерения (характеристик изучаемого объекта, расположенным в последовательности по позициям):номинальные группы – группировка опрошенных (по полу, национальности);
Слайд 37
упорядочивание в ранжированном ряду;
составление списка характеристик по
степени убывания значимости от высшего к
низшему значению
(например,
по характеру труда – ручной, производственный, интеллектуальный или
степени включенности в общественную
работу –член группы, коллектива,
сочувствующий, противник).
Слайд 38
Для них вычисляется процентная величина
ni/n*100%,
где n –
общее число респондентов, подлежащих группировке;
ni – число респондентов
в i-й группе
Слайд 39
Пример
Группировка по номинальному признаку.
Например n=600 респондентов: работники сельского
хозяйства: n1=120 человек (20%), рабочие промышленных предприятий: n2=300 (50%);
инженерно-технические работники n3=180 человек (30%).
Слайд 43
Мода
Числовой характеристикой выборки, как правило, не требующей вычислений,
является так называемая мода. Мода — это такое числовое
значение, которое встречается в выборке наиболее часто. Мода обозначается иногда как XСлайд 44 Так, например, в ряду значений (2, 6, 6,
8, 9, 9, 9, 10) модой является 9, потому
что 9 встречается чаще любого другого числа. Обратите внимание, что мода представляет собой наиболее часто встречающееся значение (в данном примере это 9), а не частоту встречаемости этого значения (в данном примере равную 3).
Слайд 45
Моду находят согласно следующим правилам:
В том случае, когда
все значения в выборке встречаются одинаково часто, принято считать,
что этот выборочный ряд не имеет моды.Например: 5, 5, 6, 6, 7, 7 — в этой выборке моды нет.
Слайд 46 Когда два соседних (смежных) значения имеют одинаковую частоту
и их частота больше частот любых других значений, мода
вычисляется как среднее арифметическое этих двух значений. Например, в выборке 1, 2, 2, 2, 5, 5, 5, 6 частоты рядом расположенных значений 2 и 5 совпадают и равняются 3. Эта частота (больше, чем частота других значений 1 и 6 (у которых она равна 1).Слайд 47 Если два несмежных (не соседних) значения в выборке
имеют равные частоты, которые больше частот любого другого значения,
то выделяют две моды. Например, в ряду 10, 11, 11, 11, 12, 13, 14, 14, 14, 17 модами являются значения 11 и 14. В таком случае говорят, что выборка является бимодальной.Слайд 48 Могут существовать и так называемые мультимодальные распределения, имеющие
более двух вершин (мод).
Если мода оценивается по множеству сгруппированных
данных, то для нахождения моды необходимо определить группу с наибольшей частотой признака. Эта группа называется модальной группой.
Слайд 49
Медиана
Медиана — обозначается X (X с волной или
Md) и определяется как величина, по отношению к которой
по крайней мере 50% выборочных значений меньше неё и по крайней мере 50% — больше.Можно дать второе определение, сказав, что медиана — это значение, которое делит упорядоченное множество данных пополам.
Слайд 50
Пример 1
Найдем медиану выборки:9, 3, 5, 8,
4,11, 13.
Решение. Упорядочим выборку по величинам
входящих в нее значений.
3, 4, 5, 8, 9, II, 13.
Поскольку в выборке семь элементов,
четвертый по порядку элемент будет иметь
значение большее, чем первые три, и меньшее,
чем последние три.
Медианой будет, четвертый элемент - 8.
Слайд 51
Пример 2.
Найдем медиану выборки: 20, 9, 13,
1,4, 11.
Решение. Упорядочим выборку:
1, 4, 9, 11, 13,
20. Поскольку здесь имеется четное число элементов, то существует две «середины» — 9 и 13. В этом случае медиана определяется как среднее арифметическое этих значений и равна будет 10.
Слайд 52
Среднее арифметическое
Среднее арифметическое ряда из п числовых значений
Х1, Х2 … Хn.. обозначается и подсчитывается как:
Слайд 53 Здесь величины 1, 2... являются так называемыми индексами.
В том случае, если отдельные значения выборки повторяются, среднюю
арифметическую вычисляют по формуле:
Слайд 54
Знак является символом операции суммирования.
Он означает, что все значения Xi. должны быть просуммированы.
Числа, стоящие над и под знаком называются пределами суммирования и указывают наибольшее и наименьшее значения индекса суммирования, между которыми расположены его промежуточные значения.
Слайд 55
Дисперсия
Рассмотрим еще одну очень важную числовую характеристику выборки,
называемую дисперсией. Дисперсия представляет собой наиболее часто использующуюся меру
рассеяния случайной величины (переменной).Дисперсия это среднее арифметическое квадратов отклонений значений переменной от её среднего значения
Слайд 57
Пример 3.
Вычислим дисперсию следующего ряда
2, 4,
6, 8, 10 (1)
Прежде всего, найдем среднее ряда (1).
Оно равно X = 6.Далее найдем
Т = (2 - 6 = -4; 4 - 6 = -2; 6 - 6 = 0; 8 - 6 = 2; 10 - 6 = 4).
Слайд 58 Так образуется новый ряд чисел. Его особенность в
том, что при сложении этих чисел обязательно получится ноль.
Проверим: (-4) + (-2) + 0 + 2 + 4 = 0.В нашем примере получится следующее:
Слайд 59
Определение процентилей
Распределение частот дает полезную для психологов информацию
об абсолютном числе, ответов по каждой из позиций. При
этом существенным недостатком описанного выше метода является отсутствие возможности сопоставить результаты обработки с данными, полученными в других исследованиях, так как общее количество опрошенных будет различаться.Слайд 60 Поэтому исследователей наряду с абсолютными величинами характеристик явления
(объекта), как правило, интересуют и относительные величины. Основные методы
их получения - расчет частот и вычисление процентных отношений.Процентное отношение - это исчисление относительной частоты в виде процентов
Слайд 62
Пример
нахождения среднее квадратичного отклонения результатов теста по
формуле:
По тесту члены группы получили следующие результаты: 5, 7,
10, 6, 8, 9, 7, 7, 9, 8
Слайд 64
Асимметрия.
Это мера ''косости'' или ''скошенности'' распределения.
Распределения, отличающиеся
одинаковыми средними и отклонениями, могут быть, тем не менее,
разными, поскольку ни модуль, ни квадрат разности не показывают, с какой стороны от среднего находилось отдельное значение случайной величины.Слайд 65 В тех случаях, когда количество значений больших среднего
превышает количество значений меньших, чем среднее, говорят о положительной
асимметрии, в противном случае – об отрицательной. Асимметрия вычисляется как отношение среднего кубов центральных отклонений к кубу стандартного отклонения:Слайд 66 В симметричном распределении асимметрия точно равна нулю, но
в зависимости от того, как изменяются разности значений со
средним, знак асимметрии меняется на положительный или отрицательный (т.к. при возведении в куб знак сохраняется).
Слайд 67
Эксцесс
Это мера ''выпуклости'' или ''крутости'' распределения. При всех
одинаковых других параметрах, два распределения могут различаться тем, что
полигон частот будет островершинным или плоским, т.е. мода может оказаться равной, но встречаться с разной частотой.Слайд 68 Эксцесс служит для того, чтобы определить крутизну кривой,
описывающей распределение, в окрестностях единственной моды, т.к. предназначен только
для унимодальных распределений.
Слайд 69
Эксцесс рассчитывается по формуле:
Особенностью всех мер рассеивания является
то, что линейное преобразование значений случайной величины никак не
сказывается на значениях этих мер, т.е. если к каждому значению случайной величины прибавляется или отнимается какое-либо число, то все отклонения, дисперсия, асимметрия и эксцесс останутся прежними
Слайд 74
Относительно данного распределения можно сказать, что: распределение унимодальное;
Основная
масса значений находится в пределах (одного стандартного отклонения) от
девятнадцати до тридцати семи, а пятьдесят процентов наблюдений – от 21 до 35.5;Слайд 75 Оно характеризуется положительной асимметрией, что означает, что более
выражены отклонения в большую от среднего арифметического сторону;
Распределение “пологое”
(отрицательный эксцесс), т.е. значения случайной величины распределены по числовой шкале достаточно равномерно.Слайд 76 Необходимо сказать, что рассчитанные в этом примере меры
могут оказаться полезными при сравнении между собой двух распределений
одной и той же случайной величины, полученных в разных условиях, и тогда можно будет заключить, в каком из двух распределений большее среднее, где рассеивание значений больше (или меньше), какие значения встречаются чаще и т.д.
Слайд 77
Тема №3
Критерии теории вероятностей
Критерий Фишера
Критерий Фишера позволяет
сравнивать величины выборочных дисперсий двух независимых выборок. Для вычисления
Fэмп нужно найти отношение дисперсий двух выборок, причем так, чтобы большая по величине дисперсия находилась бы в числителе, а меньшая – в знаменателе. Формула вычисления критерия Фишера такова:Слайд 78 где - дисперсии первой и второй выборки
соответственно.
Так как, согласно условию критерия, величина числителя должна
быть больше или равна величине знаменателя, то значение Fэмп всегда будет больше или равно единице.Число степеней свободы определяется также просто
(1)
Слайд 79 Так как, согласно условию критерия, величина числителя должна
быть больше или равна величине знаменателя, то значение Fэмп
всегда будет больше или равно единице.Число степеней свободы определяется также просто: k1=nl - 1 для первой выборки (т.е. для той выборки, величина дисперсии которой больше) и k2=n2 - 1 для второй выборки.
Слайд 80 В таблице критических значений критерия Фишера находятся по
величинам k1 (верхняя строчка таблицы) и k2 (левый столбец
таблицы).Если tэмп>tкрит, то нулевая гипотеза принимается, в противном случае принимается альтернативная
Слайд 81
Пример
В двух третьих классах проводилось тестирование умственного
развития по тесту ШТУРМА десяти учащихся. Полученные значения величин
средних достоверно не различались, однако психолога интересует вопрос — есть ли различия в степени однородности показателей умственного развития между классами
Слайд 82
Решение.
Необходимо сравнить дисперсии тестовых оценок в обоих
классах. Результаты тестирования представлены в таблице:
Слайд 83 Рассчитав дисперсии для переменных X и Y, получаем
σ2x=572,83; σ2у=174,04
Тогда по формуле (1) для расчета по
F критерию Фишера находим:
Слайд 84 По таблице из приложения для F критерия при
степенях свободы в обоих случаях равных
k=10-1=9 находим Fкрит=3,18
(<3.29), следовательно, в терминах статистических гипотез можно утверждать, что Н0 (гипотеза о сходстве) может быть отвергнута на уровне 5%, а принимается в этом случае гипотеза Н1. Иcследователь может утверждать, что по степени однородности такого показателя, как умственное развитие, имеется различие между выборками из двух классов.
Слайд 85
Фи - критерий Фишера с угловым преобразованием
Критерий
является много функциональным критерием, т.е. он применим по отношению
к самым разнообразным задачам и самым различным типам данных. Он вычисляется по формуле:
Слайд 86 где – угол, соответствующей большей процентной доле, выраженный
в радианах;
– угол, соответствующей меньшей процентной доле, выраженный в
радианах;– количество наблюдений в выборке 1;
– количество наблюдений в выборке 2.
Слайд 87
Он имеет следующие особенности:
Позволяет сравнивать две выборки или
одну и ту же выборку в разных условиях по
степени выраженности интересующего исследователя эффектаПозволяет определить сдвиг значений признака под влиянием фактора
Слайд 88 Позволяет сопоставить выборки как по качественному, так и
по количественно определяемому признаку
Минимальный объем одной из выборок может
быть равен двум, но максимальный – не ограничен, хотя в тех случаях когда выборки очень малы, достоверные различия обнаружить скорее всего не удастся.Слайд 91 Перечисленные выше статистические критерии предназначены только для сопоставления
двух распределений, вне зависимости от решаемой исследователем задачи. Помимо
этих критериев существует еще и те, которые позволяют сопоставлять три, четыре и большее количество распределений, а также решать более сложные задачи.Слайд 92 Многие ответы на вопросы могут быть получены и
при комбинированном применении статистических критериев, а также в совокупности
с другими методами математической статистики.
Слайд 93
Критерий Н-Крускала-Уоллиса
Критерий Н применяется для оценки различий по
степени выраженности анализируемого признака одновременно между тремя, четырьмя и
более выборками. Он позволяет выявить степень изменения признака в выборках, не указывая, однако, на направление этих изменений.Слайд 94 Критерий основан на том принципе, что чем меньше
взаимопересечение выборок, тем выше уровень значимости Нэмп. Следует подчеркнуть,
что в выборках может быть разное количество испытуемых, хотя в приведенных ниже задачах приводится равное число испытуемых в выборкахСлайд 95 Работа с данными начинается с того, что все
выборки условно объединяются по порядку встречающихся величин в одну
выборку и значениям этой объединенной выборки проставляются ранги. Затем полученные ранги проставляются исходным выборочным данным и по каждой выборке отдельно подсчитывается сумма рангов.Слайд 96 Критерий построен на следующей идее – если различия
между выборками незначимы, то и суммы рангов не будут
существенно отличаться одна от другой и наоборот
Слайд 97
Пример.
Четыре группы испытуемых выполняли тест Бурдона в разных
экспериментальных условиях. Задача в том, чтобы установить – зависит
ли эффективность выполнения теста от условий или, иными словами, существуют ли статистически достоверные различия в успешности выполнения теста между группами. В каждую группу входило четыре испытуемых
Слайд 98
Решение.
Число ошибок показателя переключаемое внимания в процентах
дано в таблице
Таблица 1
Слайд 99 Для дальнейшей работы с критерием необходимо выстроить все
полученные значения в один столбец по порядку и проставить
им ранги:Слайд 102 Где N – общее число членов в обобщенной
выборке;
ni – число членов в каждой отдельной выборке;
– квадраты
сумм рангов по каждой -ой выборке.Подставляем данные таблицы 3 в формулу (1) и получаем
Слайд 103 При определении критических значений критерия применительно к четырем
и более выборкам используют таблицу для критерия хи -
квадрат, подсчитав предварительно число степеней свободы v для с = 4.Тогда v = с – 1 = 4 – 1=3.
Находим по таблице Нкр и представляем в привычном виде:
Слайд 105 Переформулируем полученный результат в терминах нулевой и альтернативной
гипотез: поскольку между показателями, измеренными в четырех разных условиях,
существуют лишь случайные различия, то принимается нулевая гипотеза Н0, т.е. гипотеза о сходстве.Слайд 106 Иными словами, различные условия проведения теста Бурдона не
влияют на показатели переключаемости внимания. Подчеркнем, что если использовать
критерии, позволяющие сравнивать только два ряда значений, то полученный выше результат потребовал бы шести сравнений – первая выборка со второй, третьей и т.д.
Слайд 107
Для использование критерия Н необходимо соблюдать следующие условия:
1.
Измерение должно быть проведено в шкале порядка, интервалов или
отношений.2. Выборки должны быть независимыми.
3. Допускается разное число испытуемых в сопоставляемых выборках.
4.При сопоставлении трех выборок допускается, чтобы в одной из них было n =3, а в двух других n=2.
Однако в таком случае различия могут быть зафиксированы лишь на 5 % уровне значимости.
Слайд 108 5. Таблица критериев только для трех выборок, то
есть максимальное число испытуемых во всех трех выборках может
быть меньше и равно 5.6. При большем числе выборок и разном количестве испытуемых в каждой выборке следует пользоваться таблицей Приложения для критерия хи - квадрат. В этом случае число степеней свободы при этом определяется по формуле: v = с – 1, где с – количество сопоставляемых выборок
Слайд 109
– критерий Вилкоксона.
Этот критерий применяется для решения тех
же задач, что и критерий знаков, но он позволяет
оценить не только направление сдвига, но и его интенсивность, особенно, если вариации признака ярко выражены. Он основан на подсчете суммы рангов значений сдвигов случайной величины с более редким (или менее ожидаемым) знаком:
Слайд 111
Тема №4
Корреляционный анализ.
Взаимосвязи на языке математики обычно описываются
при помощи функций, которые графически изображаются в виде линий.
На рис.1 изображено несколько графиков функций. Если изменение одной переменной на одну единицу всегда приводит к изменению другой переменной на одну и ту же величину, функция является линейной (график ее представляет прямую линию); любая другая связь — нелинейная.Слайд 113 Если увеличение одной переменной связано с увеличением другой,
то связь — положительная (прямая); если увеличение одной переменной
связано с уменьшением другой, то связь — отрицательная (обратная). Если направление изменения одной переменной не меняется с возрастанием (убыванием) другой переменной, то такая функция — монотонная; в противном случае функцию называют немонотоннойСлайд 114 Функциональные связи, подобные изображенным на рис.1, являются идеализациями.
Их особенность заключается в том, что одному значению одной
переменной соответствует строго определенное значение другой переменной. Например, такова взаимосвязь двух физических переменных - веса и длины тела (линейная положительная).Слайд 115 Однако даже в физических экспериментах эмпирическая взаимосвязь будет
отличаться от функциональной связи в силу неучтенных или неизвестных
причин: колебаний состава материала, погрешностей измерения.
Слайд 116
Особенности коэффициента корреляции
Коэффициент корреляции показывает сразу два параметра
статистической связи – ее направление и тесноту. Направление связи
может быть положительным, когда большему значению одной переменной соответствует большее значение другой переменной и отрицательным, когда большему одной переменной соответствует меньшее значение другой переменнойСлайд 117 Коэффициент корреляции всегда находится в пределах от –
1 до +1. При этом, если он оказывается положительным,
то говорят о положительной корреляции между двумя переменными, а если отрицательным – то, соответственно об отрицательной. Абсолютное значение коэффициента корреляции показывает тесноту или степень выраженности такой связи.Слайд 118 При коэффициенте корреляции равном нулю признается отсутствие связи,
но даже тогда, когда он оказывается больше нуля, еще
не следует делать вывод о наличии корреляционной связи. О связи между двумя переменными можно говорить лишь в том случае, если значение коэффициента корреляции оказывается выше критического для соответствующего числа наблюдений,Слайд 119 если речь идет о положительной связи, и ниже
критического, если–об отрицательной.
Необходимо подчеркнуть, что коэффициент корреляции предназначен лишь
для измерения линейных связей между переменными. Слайд 120 По этой причине в реальных условиях почти невозможно
получить коэффициент корреляции равный единице.
Например, если рассчитать коэффициент
корреляции между расстоянием планет Солнечной системы от Солнца и их периодом обращения, то коэффициент корреляции окажется равным 0,998, несмотря на то, что связь здесь прямая: чем дальше планета удалена от Солнца, тем больше ее период обращения. Слайд 121 Причина этого заключается в том, что связь между
расстоянием от Солнца и периодом обращения для планет Солнечной
системы на графике отображается не прямой, а слегка изогнутой линией, следуя известным законам небесной механики И. Кеплера.Слайд 122 Что касается психологических измерений, то здесь коэффициент корреляции
равный 0,8 – 0,9 признается достаточно высоким, а связь
статистически значимой (достоверной) даже для небольшого числа наблюдений. Например, если при первичном и повторном тестировании большая часть испытуемых показала один и тот же результат по тесту X, и коэффициент корреляции оказался в указанных пределах,Слайд 123 то тест может быть признан надежным, несмотря на
то, что у части испытуемых результат повторного тестирования отличался
от первичногоВ реальных экспериментальных условиях наличие небольшого разброса данных может свидетельствовать не об отсутствии связи, а о некоторой ошибке измерения, или влиянии неучтенного фактора на исход эксперимента.
Слайд 124
Коэффициент корреляции « »
При сравнении двух
переменных, измеренных в дихотомической шкале, мерой корреляционной связи служит
так называемый коэффициент « », или, как назвал эту статистику ее автор К. Пирсон, – «коэффициент ассоциации». Величина коэффициента « » лежит в интервале +1 и –1. Он может быть как положительным, так и отрицательным, характеризуя направление связи двух дихотомически измеренных признаков.
Слайд 125
ПРИМЕР
Влияет ли семейное положение на успешность учебы
студентов-мужчин?
Решение. Для решения этой задачи психолог выясняет у
12 студентов-мужчин, во-первых, женат он или холост, соответственно проставляя каждому 1 – женат или 0 – холост, и, во-вторых, насколько успешно тот учится: успешной учебе проставляется код 0, при наличии академических задолженностей проставляется код 1. Для решения данные лучше свести в таблицу
Слайд 127
где рх – частота или доля признака, имеющего
1 по X, (1 – рх) – доля или
частота признака, имеющего 0 по X; ру – частота или доля признака, имеющего1 по Y, (1 –ру) – доля или частота признака, имеющего 0 по Y, рху – доля или частота признака, имеющая 1 одновременно как по Х так и по Y.
Слайд 128 Частоты вычисляется следующим образом: подсчитывается количество 1 в
переменной X и полученная величина делится на общее число
элементов этой переменной – N.Аналогично подсчитываются частоты для переменной Y. Обозначение рху – соответствует частоте или доле признаков, имеющих единицу как по Х таки по Y.
Слайд 129 Пусть рх соответствует доли студентов, имеющих 1 по
X, тогда рх = 5 : 12= 0,4167 (пять
единичек, поделенных на общее число студентов, принявших участие в эксперименте).В этом случае (1 – рх) = 1 –0,4167 = 0,5833. Пусть обозначение ру – соответствует доли студентов, имеющих1 по Y, тогда ру = 6 : 12 = 0,5.
В этом случае (1 – ру) = 1 – 0,5 = 0,5.
Слайд 130 Подсчитаем рху – долю студентов, имеющих единицу как
по Х так и по Y.
В нашем случае
рху = 4 : 12= 0,3333. Подставляем полученные величины в формулу (1), получаем 0,507.
Поскольку, как мы уже указывали выше, для этого коэффициента корреляции нет таблиц значимости, рассчитываем его значимость по формуле ТФ
Слайд 131 Число степеней свободы в нашем случае будет равно
k = n– 1 = 12 – 2 =
10.По таблице Приложения для k = 10 находим критические значения критерия Стьюдента, они равны соответственно для Р<0,05 tкр= 2,23 и для Р<0,01 tкp= 4,59. Значение величины Тф попало в зону не значимости.
Слайд 132 Иными словами, психолог не обнаружил никакой связи между
успешностью обучения и семейным положением студентов. Или, в терминах
статистических гипотез, гипотеза Н1, отклоняется и принимается гипотеза Н0 о сходстве коэффициента корреляции « » с нулем. Отметим, что кодирование, т.е. приписывание чисел 0 или 1 тому или иному признаку, было произвольным.
Слайд 133
ЛИТЕРАТУРА
Основная:
Сидоренко Е.В. Методы математической обработки в психологии. М.,
2001.
(Биб. ИнЕУ).
Ермалаев О.Ю. Математическая статистика для психологов. М., 2002.
(Биб. ИнЕУ).
Гмурман В.С. Теория вероятностей и математическая статистика. В.Ш., М.,1999. (Биб. ИнЕУ).
Слайд 134
Дополнительная:
Шевандрин Н.И. Психодиагностика, коррекция и развитие личности. М.,1998.
Немов
Р.С. Психология (книга 3) М.,1998. (Биб. ИнЕУ).
Логвиненко А.Д. Измерения
в психологии: математические основы. М., 1993.Дружинин В.И. Экспериментальная психология. М., 1997.