- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Математический бой
Содержание
- 2. Правила ведения боя.Команды по очереди вызывают друг
- 3. Ход боя.Первая команда вызывает вторую на решение
- 4. Цели: проверка знаний и навыков по решению квадратных
- 5. Из истории решения квадратных уравнений.Найденные древние вавилонские
- 6. Задачи для проведения математического боя
- 7. Задача № 1Задача № 2Задача № 3Задача
- 8. Установите соответствие между видом уравнения в левой колонке
- 9. 2. Выберите уравнения, являющееся квадратным. (
- 10. 3. Выберите уравнение, не являющееся квадратным.
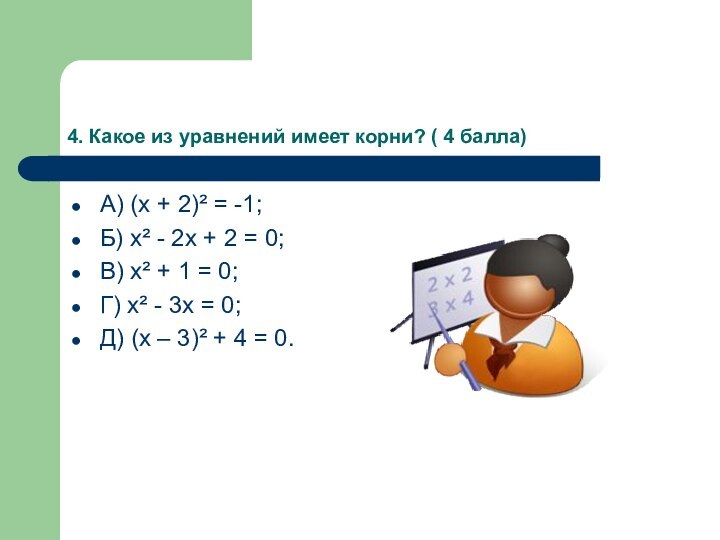
- 11. 4. Какое из уравнений имеет корни? (
- 12. 5. Какое из уравнений не имеет корней?
- 13. 6. Выберите верное утверждение. ( 6 баллов)А)
- 14. 7. Решите уравнение ( 6 баллов) 5х² - 10х + 1 = 0
- 15. 8. Найдите отрицательный корень уравнения. ( 6 баллов) 4х² + 4х = 3 = 0
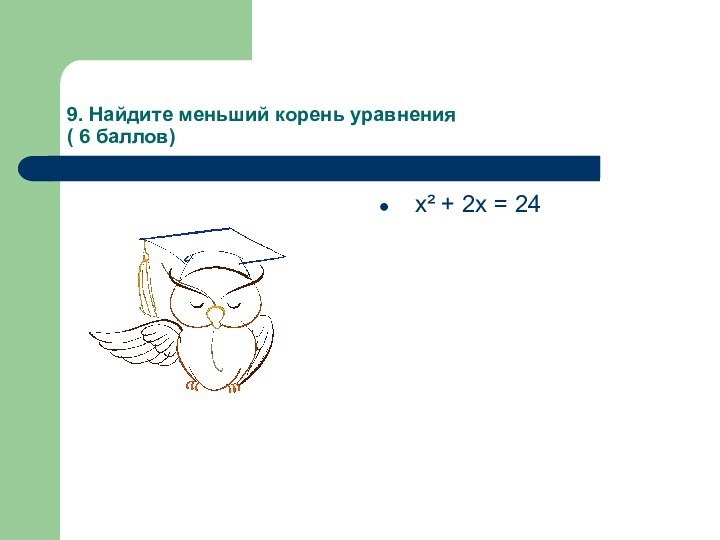
- 16. 9. Найдите меньший корень уравнения ( 6 баллов) х² + 2х = 24
- 17. 10. Решите уравнение (6 баллов) 3х + 0,4х² + 0
- 18. 11. Решите уравнение ( 8 баллов) ( х – 5) ² = 5(9 – 2х)
- 19. 12. Найдите сумму корней этого уравнения.
- 20. 13. Укажите наименьшее значение а, при котором
- 21. 14. Решите уравнение ( 10 баллов)х² - 3√3 х – 12 = 0
- 22. 15. Решите уравнение ( 10 баллов)х - 11√х – 12 = 0
- 23. 16. Решите уравнение ( 8 баллов) (2х² - 5х – 3)√х = 0
- 24. 17. ( 8 баллов) Возраст сына и
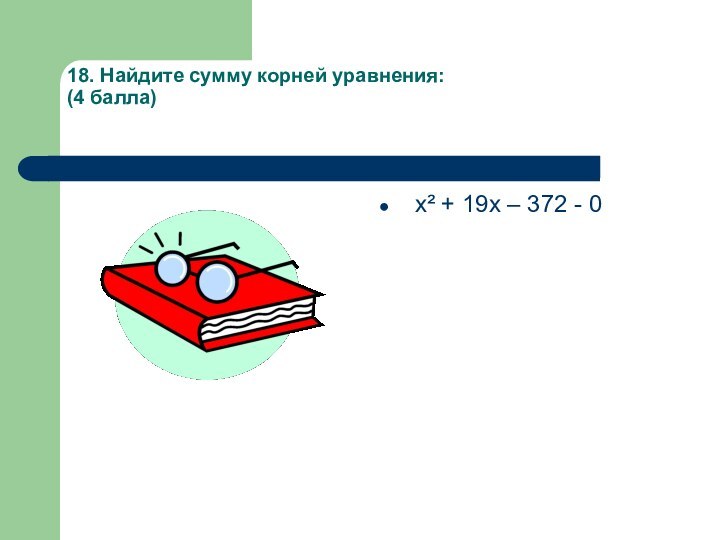
- 25. 18. Найдите сумму корней уравнения: (4 балла) х² + 19х – 372 - 0
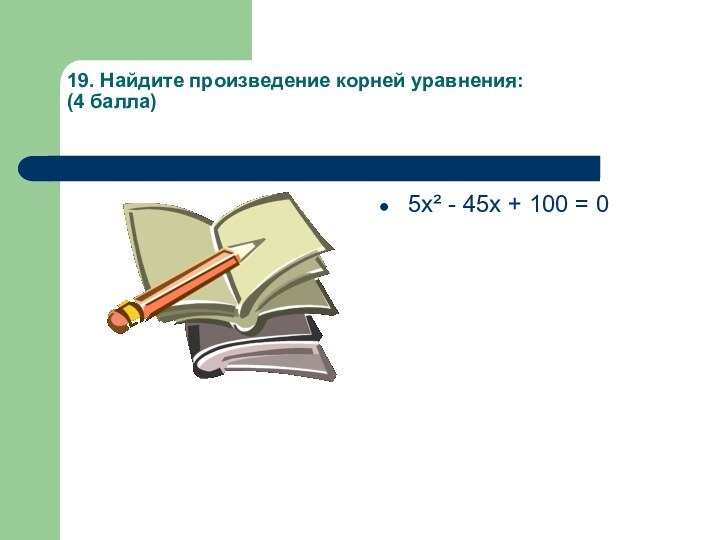
- 26. 19. Найдите произведение корней уравнения: (4 балла) 5х² - 45х + 100 = 0
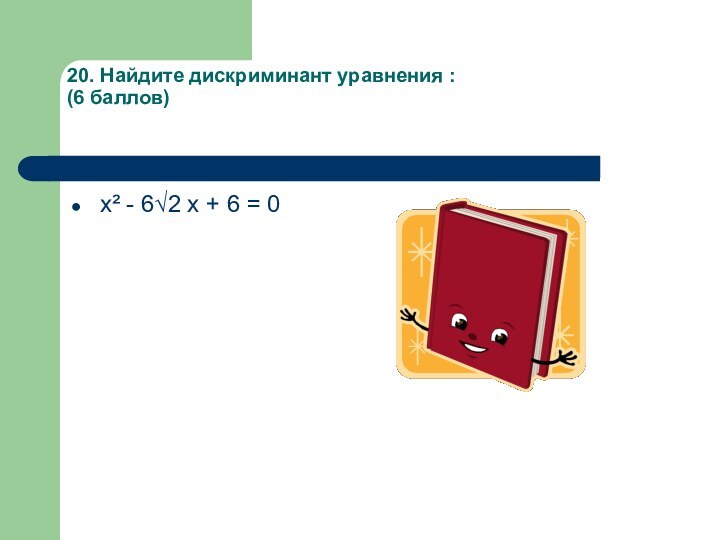
- 27. 20. Найдите дискриминант уравнения : (6 баллов) х² - 6√2 х + 6 = 0
- 28. 21. При каком значении r корни квадратного
- 29. 22. Решить уравнение (16 баллов)х² - 3│х│ =0
- 30. 23. Решить уравнение ( 16 баллов)4х² - 3│х│+ х =0
- 31. 24. Составьте квадратное уравнение, ( 6
- 32. 25. Не вычисляя корней уравнения ( 10
- 33. Скачать презентацию
- 34. Похожие презентации
Правила ведения боя.Команды по очереди вызывают друг друга на решение задач (задачи за одну неделю вывешены в классе на стенде). Стоимость каждой задачи оценивается в баллах.



























Слайд 3
Ход боя.
Первая команда вызывает вторую на решение какой-то
задачи. На кон ставится стоимость этой задачи. В случае,
если вторая команда дает правильное решение, она получает себе стоимость этой задачи и право следующего вызова. В случае, если она задачу не решает, она платит штраф в половину стоимости задачи. После этого решение обязана дать первая команда. За правильное решение она получает весь выигрыш и право следующего вызова. Если же она решения не знает, то платит штраф в стоимость этой задачи.
Слайд 4
Цели:
проверка знаний и навыков по решению квадратных уравнений
и по применению их к решению задач; формирование умений
и навыков по обобщению и систематизации знаний; развитие внимания, сообразительности, быстроты реакции, логики, мышления; воспитание чувства ответственности, дисциплинированности, аккуратности.
Слайд 5
Из истории решения квадратных уравнений.
Найденные древние вавилонские глиняные
таблички, датированные где-то между 1800 и 1600 годами до
н.э., являются самыми ранними свидетельствами об изучении квадратных уравнений. На этих же табличках изложены методы решения некоторых типов квадратных уравнений.Древнеиндийский математик Баудхаяма в VIII столетии до н.э. впервые использовал квадратные уравнения в форме ax2 = c и ax2 + bx = c и привел методы их решения.
Вавилонские математики примерно с IV века до н.э. и китайские математики примерно со II века до н.э. использовали метод дополнения квадрата для решения уравнений с положительными корнями. Около 300 года до н.э. Эвклид придумал более общий геометрический метод решения.
Первым математиком, который нашел решения уравнения с отрицательными корнями в виде алгебраической формулы, был Брахмагупта (Индия, VII столетие нашей эры).
Слайд 7
Задача № 1
Задача № 2
Задача № 3
Задача №
4
Задача № 5
Задача № 6
Задача № 7
Задача № 8
Задача
№ 9Задача № 10
Задача № 11
Задача № 12
Задача № 13
Задача № 14
Задача № 15
Задача № 16
Задача № 17
Задача № 18
Задача № 19
Задача № 20
Задача № 21
Задача № 22
Задача № 23
Задача № 24
Задача № 25
Слайд 8 Установите соответствие между видом уравнения в левой колонке с
его названием в правой колонке.
( 4балла)
ах²+вх+с=0
ах²+с=0 х²+вх+с=0неполное
приведенное
квадратное
Слайд 9
2. Выберите уравнения, являющееся квадратным.
( 4 балла)
а)
х² - 4 = ( х – 2)²;
б) х²
- х = 0;в) 17х + 4 = 0;
г) 0х² + 15х + 2 = 0;
д) – 8х³ + 2 = 0.
Слайд 10 3. Выберите уравнение, не являющееся квадратным. ( 4
балла)
А) х² + х = 0;
Б) 2х² - х
– 1 = 0;В) х² – 5 = 0;
Г) х² - ( х – 1)² = 0;
Д) 3х² + 17х – 20 = 0.
Слайд 11 4. Какое из уравнений имеет корни? ( 4
балла)
А) (х + 2)² = -1;
Б) х² - 2х
+ 2 = 0;В) х² + 1 = 0;
Г) х² - 3х = 0;
Д) (х – 3)² + 4 = 0.
Слайд 12 5. Какое из уравнений не имеет корней? (
4 балла)
А) х² + 3х = 0;
Б) х² +
2х + 1 = 0;В) х² + 4 = 0;
Г) (х + 2) ² = 0;
Д) (х + 3) ² - 4 = 0.
Слайд 13
6. Выберите верное утверждение. ( 6 баллов)
А) уравнение
вида ах² + вх + с = 0, где
а,в,с – заданные числа и в≠0, х- неизвестное, называется квадратным;Б) уравнение х² = а имеет корни при а‹0;
В) х = 3 является корнем уравнения
(х² - 9):(х – 3) = 0;
Г) х² - 2х + 3 = (х – 2) ² - 1;
Д) квадратное уравнение ах² + вх + с = 0 называется неполным, если один из коэффициентов в или с равен 0.
Слайд 19 12. Найдите сумму корней этого уравнения. ( 8
баллов)
Один из корней уравнения
х² + рх – 28
= 0 равен 7. Слайд 20 13. Укажите наименьшее значение а, при котором уравнение(10
баллов)
7х² + ах + 7 = 0 имеет единственный
корень.
Слайд 24
17. ( 8 баллов)
Возраст сына и папы в
сумме составляет 31 год, а произведение их возрастов равно
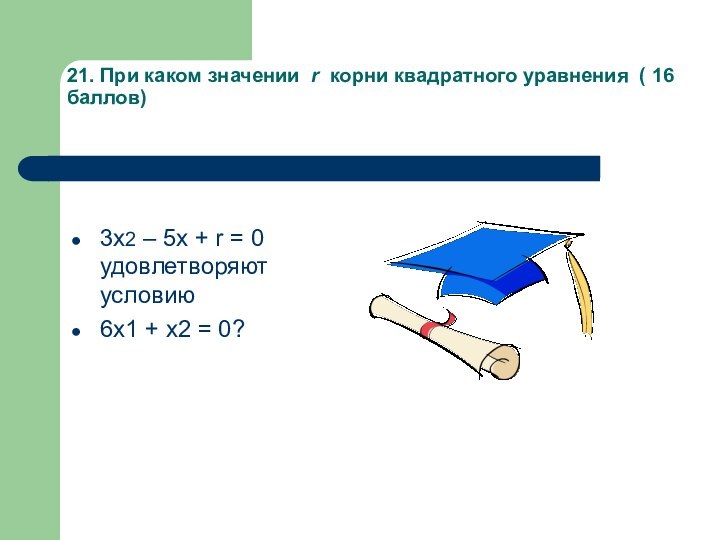
84. Сколько лет сыну?Слайд 28 21. При каком значении r корни квадратного уравнения
( 16 баллов)
3х2 – 5х + r = 0
удовлетворяют условию 6х1 + х2 = 0?





























