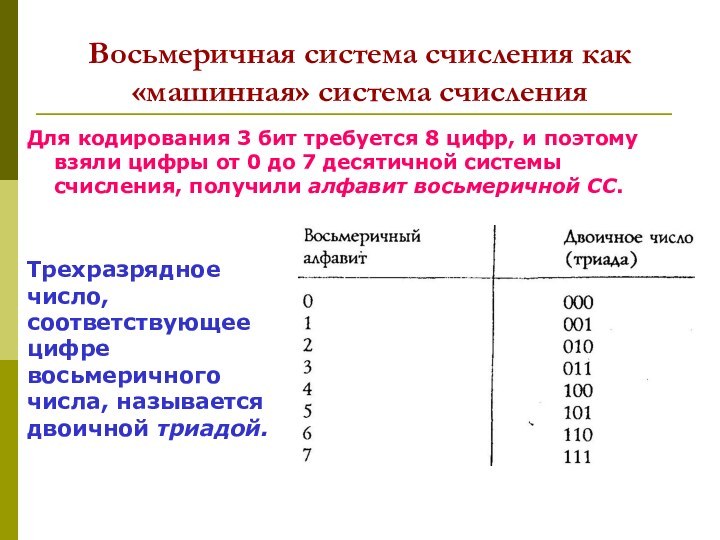
счисления:
1) 101012 + 1012
2) 101012 + 10102
3) 1000012 –
11024) 10101002 – 112
5) 111112 + 10012
1) 110102 + 10112
2) 101012 + 10112
3) 1000102 – 1012
4) 10100012 – 1012
5) 1010112 + 1102