- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Осевая симметрия
Содержание
- 2. На рисунке – бумажная салфетка, сложенная вчетверо. Нарисовать, как будет выглядеть салфетка, если её развернуть.Задача №1
- 4. На рисунке – бумажная салфетка, сложенная вчетверо. Нарисовать, как будет выглядеть салфетка, если её развернуть.Задача №2
- 6. Я в листочке, я в кристалле,Я в
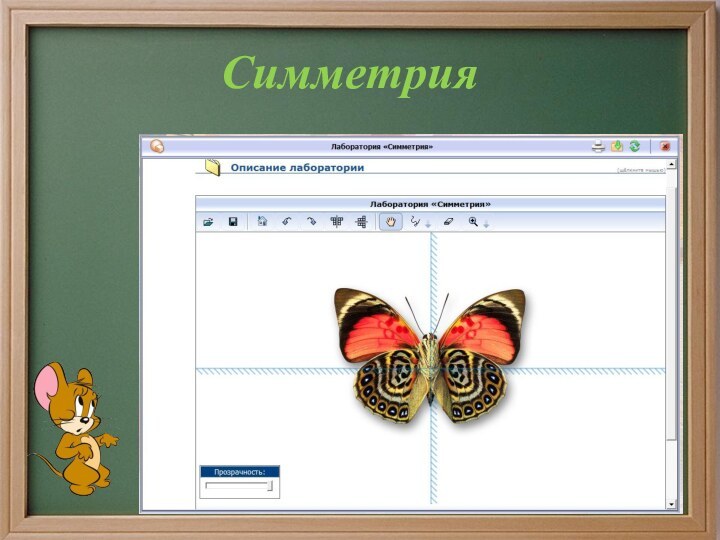
- 7. Симметрия
- 8. Симметрия в природеВнимательное наблюдение показывает, что основу красоты многих форм, созданных природой, составляет симметрия.
- 9. Симметрия в растительном мире
- 10. Симметрия в животном мире.
- 11. Симметрия является фундаментальным свойством природы, представление о котором слагалось в течение десятков, сотен, тысяч поколений.
- 12. В мир неживой природы очарование симметрии вносят
- 14. Симметрия в архитектуре России
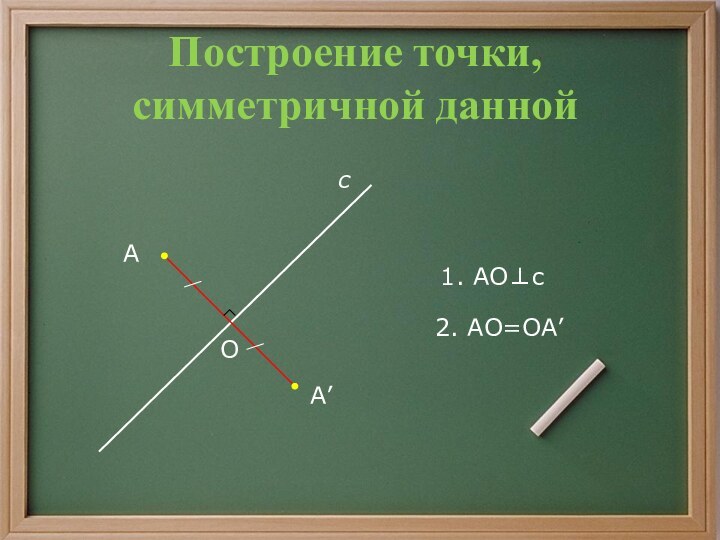
- 15. Построение точки, симметричной данной1. АОсО2. АО=ОА’
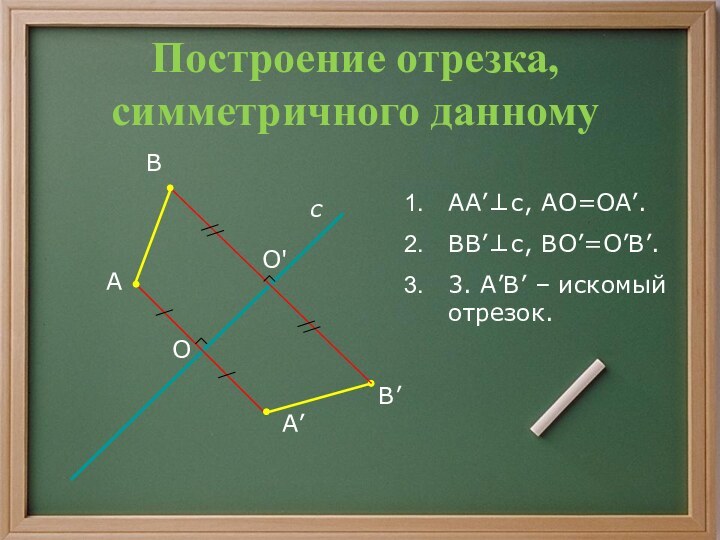
- 16. Построение отрезка, симметричного данномуАА’с, АО=ОА’.ВВ’с, ВО’=О’В’.3. А’В’ – искомый отрезок.
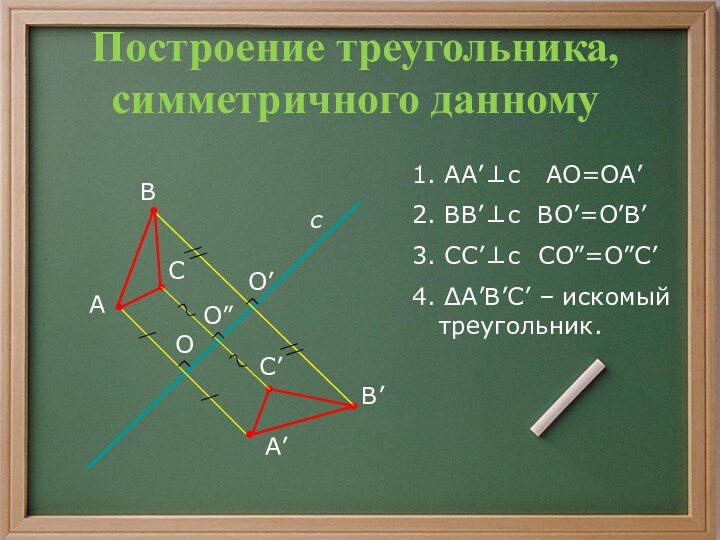
- 17. Построение треугольника, симметричного данному1. AA’c AO=OA’2. BB’c BO’=O’B’3. СС’c СO”=O”С’4. A’B’С’ – искомый треугольник.
- 18. № 474; №480; №481
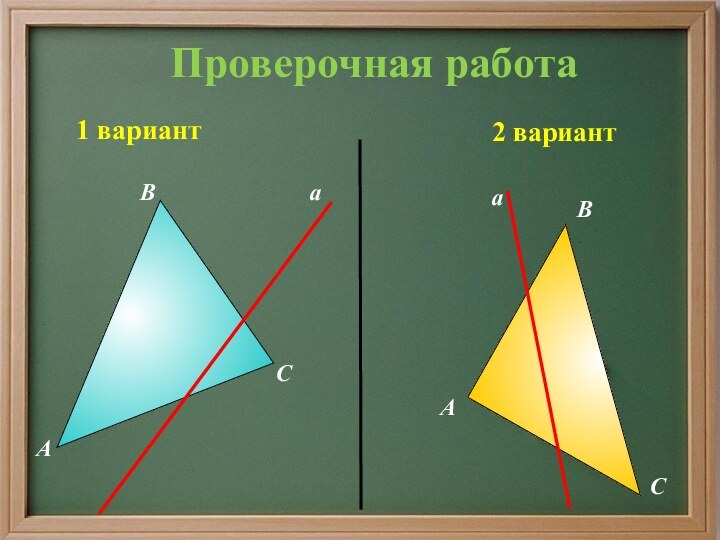
- 19. 1 вариант2 вариантаАВСаАВСПроверочная работа
- 20. Имеют ли оси симметрии фигуры и если да, то сколько?
- 21. Скачать презентацию
- 22. Похожие презентации
На рисунке – бумажная салфетка, сложенная вчетверо. Нарисовать, как будет выглядеть салфетка, если её развернуть.Задача №1















Слайд 2 На рисунке – бумажная салфетка, сложенная вчетверо. Нарисовать,
как будет выглядеть салфетка, если её развернуть.
Слайд 4 На рисунке – бумажная салфетка, сложенная вчетверо. Нарисовать,
как будет выглядеть салфетка, если её развернуть.
Задача №2
Слайд 6
Я в листочке, я в кристалле,
Я в живописи,
архитектуре,
Я в геометрии, я в человеке.
Одним я нравлюсь, другие
Находят
меня скучной.Но все признают, что
Я – элемент красоты.
Слайд 8
Симметрия в природе
Внимательное наблюдение показывает, что основу красоты
многих форм, созданных природой, составляет симметрия.
Слайд 11 Симметрия является фундаментальным свойством природы, представление о котором
слагалось в течение десятков, сотен, тысяч поколений.
Слайд 12 В мир неживой природы очарование симметрии вносят кристаллы.
Каждая снежинка- это маленький кристалл замерзшей воды. Форма снежинок
может быть очень разнообразной, но все они обладают симметрией .Симметрия в
неживой природе