Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему Математика в природе

Содержание

2. Основополагающий вопросВ чем единство математики, искусства и красоты природы?
3. Возможен ли мир без симметрии?Малайзия, Куала Лумпур башни-близнецы компании «Петронас», Париж, Эйфелева башняПроблемный вопрос:
4. Цель проекта:Познакомится с понятием симметрии
5. Задачи:Поиск информации о симметрииРассмотреть основные понятияИзучить виды симметрииВыяснить важность симметрии для нас
6. "Симметрия является той идеей, посредством которой человек
7. Симметрия в природе – следствие необходимости сохранять
8. Что же такое симметрия?В древности слово «симметрия»
9. Виды симметрии в школьном курсе геометрии Симметрия относительно прямойСимметрия относительно точкиСимметрия относительно плоскости
10. Симметрия относительно точкиФигура называется симметричной относительно точки,
11. Центральную симметрию можно встретить повсюду
12. Фигура называется симметричной относительно прямой, если для
13. Осевая симметрия присутствует чуть ли не в
14. Осевая симметрия в живой природе
15. Если преобразование симметрии относительно плоскости переводит фигуру
16. Часто такую симметрию называют зеркальной. А зеркало
17. Нетрадиционные виды симметрии Винтовая симметрия Симметрия поворота Переносная симметрия
18. Винтовая симметрия
19. Переносная симметрия или скользящее преобразование
20. Симметрия поворота
21. Свойства симметрииСимметрия многолика. Она обладает свойствами, которые
22. Симметрия треугольниковРавностороннй треугольникТождественное преобразование Е
23. Симметрия четырехугольниковЧетырёхугольникТождественное преобразование ЕРомбТождественное преобразование ЕОсевая симметрия
24. Круг и шарКруг и шар – самые совершенные из фигур. Эти фигуры обладают бесконечным множеством симметрий.
25. Распределение фигур по классам симметрииРаспределение по классам
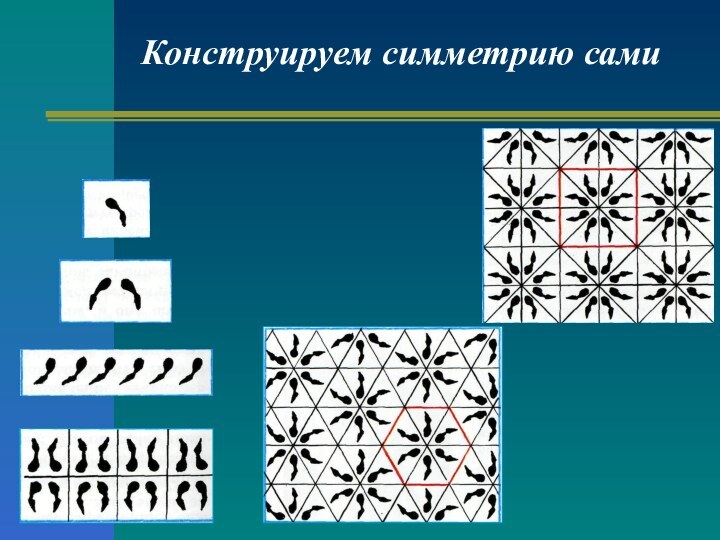
26. Конструируем симметрию сами
27. Симметрия танца
28. Симметрия и асимметрияСимметрия и асимметрия - это
29. Примером удивительного сочетания симметрии и асимметрии является
30. Скачать презентацию
31. Похожие презентации

Основополагающий вопросВ чем единство математики, искусства и красоты природы?

Возможен ли мир без симметрии?Малайзия, Куала Лумпур башни-близнецы компании «Петронас», Париж, Эйфелева башняПроблемный вопрос:

Цель проекта:Познакомится с понятием симметрии

Задачи:Поиск информации о симметрииРассмотреть основные понятияИзучить виды симметрииВыяснить важность симметрии для нас

Симметрия в природе – следствие необходимости сохранять устойчивость. Симметрия лежит в основе

Что же такое симметрия?В древности слово «симметрия» употреблялось в значении «гармония», «красота».

Виды симметрии в школьном курсе геометрии Симметрия относительно прямойСимметрия относительно точкиСимметрия относительно плоскости

Симметрия относительно точкиФигура называется симметричной относительно точки, если для каждой точки фигуры

Центральную симметрию можно встретить повсюду

Фигура называется симметричной относительно прямой, если для каждой точки фигуры симметричная ей

Осевая симметрия присутствует чуть ли не в каждом архитектурном объектеФрагмент чугунной решётки

Если преобразование симметрии относительно плоскости переводит фигуру в себя, то фигура называется

Часто такую симметрию называют зеркальной. А зеркало не просто копирует объект, но

Нетрадиционные виды симметрии Винтовая симметрия Симметрия поворота Переносная симметрия

Переносная симметрия или скользящее преобразование

Свойства симметрииСимметрия многолика. Она обладает свойствами, которые одновременно и просты, и сложны,

Симметрия треугольниковРавностороннй треугольникТождественное преобразование Е Осевая симметрия

Симметрия четырехугольниковЧетырёхугольникТождественное преобразование ЕРомбТождественное преобразование ЕОсевая симметрия S1,S2Повороты отн. О на 1800КвадратТождественное

Круг и шарКруг и шар – самые совершенные из фигур. Эти фигуры обладают бесконечным множеством симметрий.

Распределение фигур по классам симметрииРаспределение по классам симметрий дает нам новый взгляд

Симметрия и асимметрияСимметрия и асимметрия - это две формы проявления одной и

Примером удивительного сочетания симметрии и асимметрии является Храм Василия Блаженного.Это композиция из

Природа – наука – искусствоИтак, сфера влияния симметрии поистине безгранична. Природа –

Слайды презентации

Слайд 2 Основополагающий вопрос
В чем единство математики, искусства и красоты

природы?

Слайд 3 Возможен ли мир без симметрии?
Малайзия, Куала Лумпур башни-близнецы

компании «Петронас»,
Париж, Эйфелева башня
Проблемный вопрос:

Слайд 4 Цель проекта:
Познакомится с понятием симметрии

Слайд 5 Задачи:
Поиск информации о симметрии
Рассмотреть основные понятия
Изучить виды симметрии
Выяснить

важность симметрии для нас

Слайд 6 "Симметрия является той идеей, посредством которой человек на

протяжении веков пытался постичь и создать порядок, красоту и

совершенство.”
(Г. Вейль)

Г. Ессентуки Источник минеральной воды

Ватикан Площадь Святого Петра

Слайд 7 Симметрия в природе – следствие необходимости сохранять устойчивость.

Симметрия в природе – следствие необходимости сохранять устойчивость. Симметрия лежит в

Симметрия лежит в основе законов сохранения. Можно сказать, что

симметрия – это проявление стремления материи к надёжности и прочности.

Российский самолёт ТУ-154

Автомобиль Renault

Слайд 8 Что же такое симметрия?
В древности слово «симметрия» употреблялось

Что же такое симметрия?В древности слово «симметрия» употреблялось в значении «гармония»,

в значении «гармония», «красота».
Будем называть симметрией фигуры, любое

преобразование, переводящее фигуру в себя, т.е. обеспечивающее ее самосовмещение.

Найденное в гробнице Тутанхомона нагрудное украшение со священными знаками должно было гарантировать фараону воскрешение.

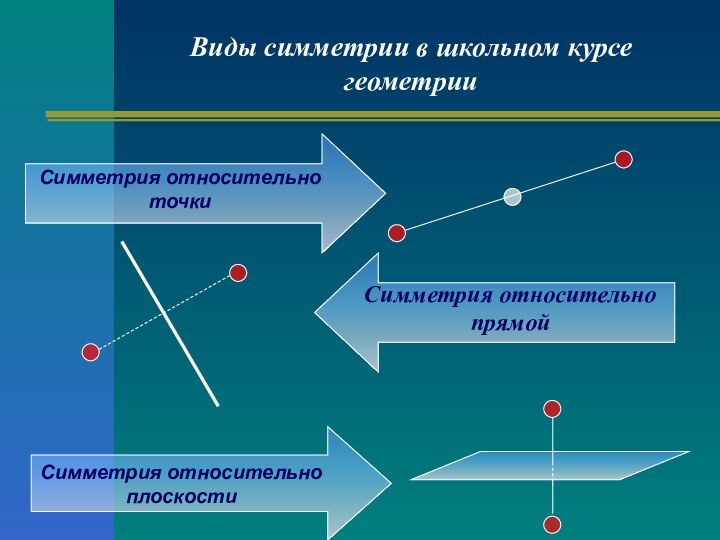
Слайд 9 Виды симметрии в школьном курсе геометрии
Симметрия относительно

прямой
Симметрия относительно точки
Симметрия относительно плоскости

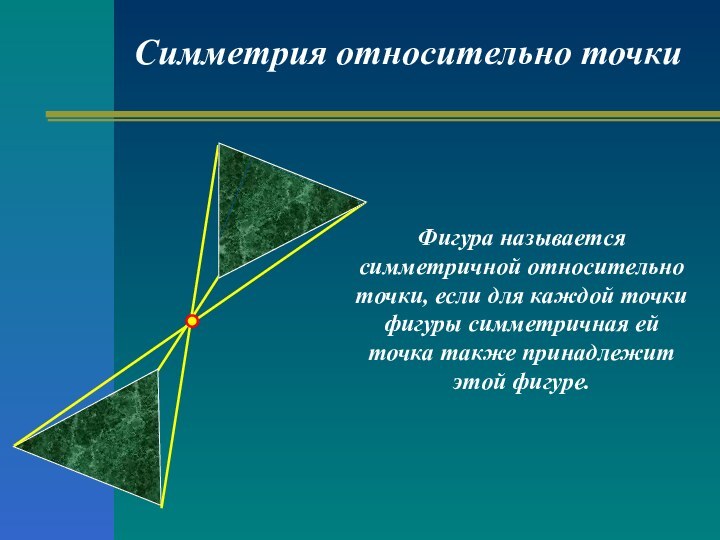
Слайд 10 Симметрия относительно точки
Фигура называется симметричной относительно точки, если

Симметрия относительно точкиФигура называется симметричной относительно точки, если для каждой точки

для каждой точки фигуры симметричная ей точка также принадлежит

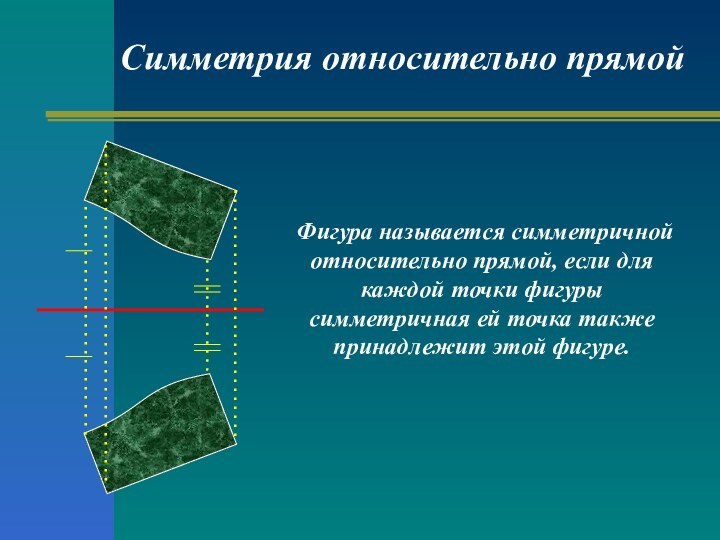
этой фигуре.

Слайд 11 Центральную симметрию можно встретить повсюду

Слайд 12 Фигура называется симметричной относительно прямой, если для каждой

точки фигуры симметричная ей точка также принадлежит этой фигуре.

Симметрия

относительно прямой

Слайд 13 Осевая симметрия присутствует чуть ли не в каждом

Осевая симметрия присутствует чуть ли не в каждом архитектурном объектеФрагмент чугунной

архитектурном объекте
Фрагмент чугунной решётки ворот Таврического дворца в Санкт-Петербурге
г.Ессентуки

Грязелечебница

Германия Бонн Университет

Слайд 14 Осевая симметрия в живой природе

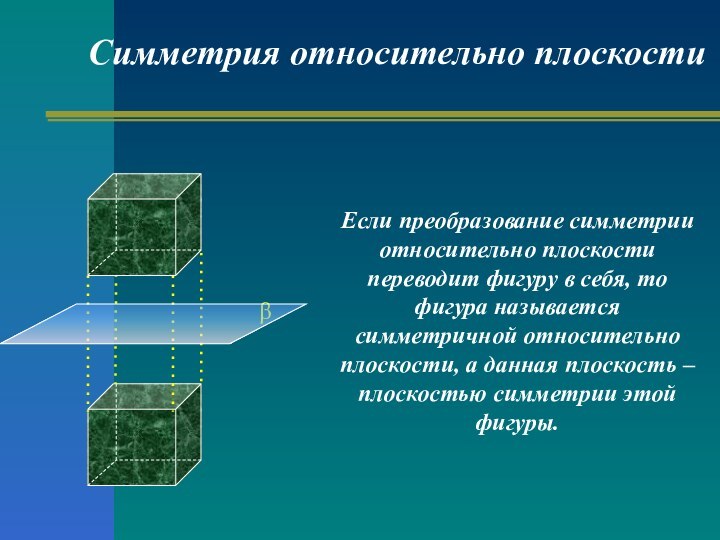
Слайд 15 Если преобразование симметрии относительно плоскости переводит фигуру в

Если преобразование симметрии относительно плоскости переводит фигуру в себя, то фигура

себя, то фигура называется симметричной относительно плоскости, а данная

плоскость – плоскостью симметрии этой фигуры.

Симметрия относительно плоскости

Слайд 16 Часто такую симметрию называют зеркальной. А зеркало не

Часто такую симметрию называют зеркальной. А зеркало не просто копирует объект,

просто копирует объект, но и меняет местами передние и

задние части объекта по отношению к зеркалу.

Дубаи Башни Эмиратов

Соловецкий монастырь

Германия Гамбург

Слайд 17 Нетрадиционные виды симметрии
Винтовая симметрия

Симметрия поворота

Переносная

симметрия

Слайд 18 Винтовая симметрия

Слайд 19 Переносная симметрия или скользящее преобразование

Слайд 20 Симметрия поворота

Слайд 21 Свойства симметрии
Симметрия многолика. Она обладает свойствами, которые одновременно

Свойства симметрииСимметрия многолика. Она обладает свойствами, которые одновременно и просты, и

и просты, и сложны, способны проявляться и единожды, и

бесконечно много раз. Даже человек, мало знакомый с геометрией, легко выберет из предложенных ему фигур наиболее симметричные.

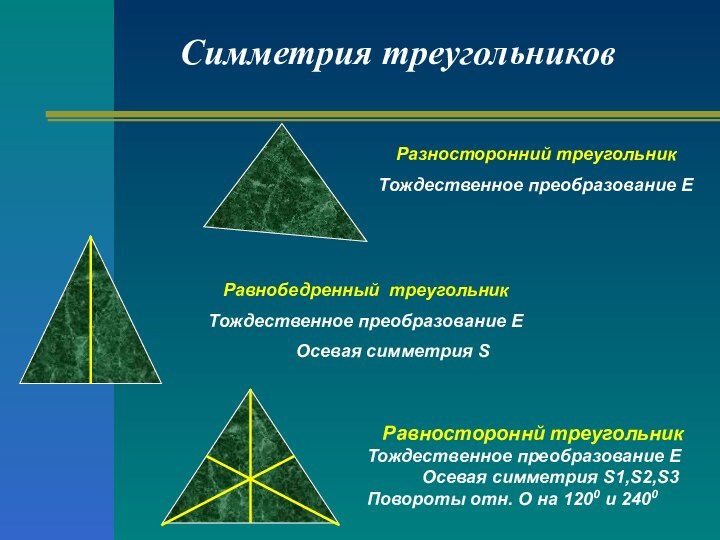
Слайд 22 Симметрия треугольников
Равностороннй треугольник
Тождественное преобразование Е

Симметрия треугольниковРавностороннй треугольникТождественное преобразование Е Осевая симметрия S1,S2,S3Повороты отн.

Осевая симметрия S1,S2,S3
Повороты отн. О на 1200

и 2400

Разносторонний треугольник
Тождественное преобразование Е

Равнобедренный треугольник
Тождественное преобразование Е
Осевая симметрия S

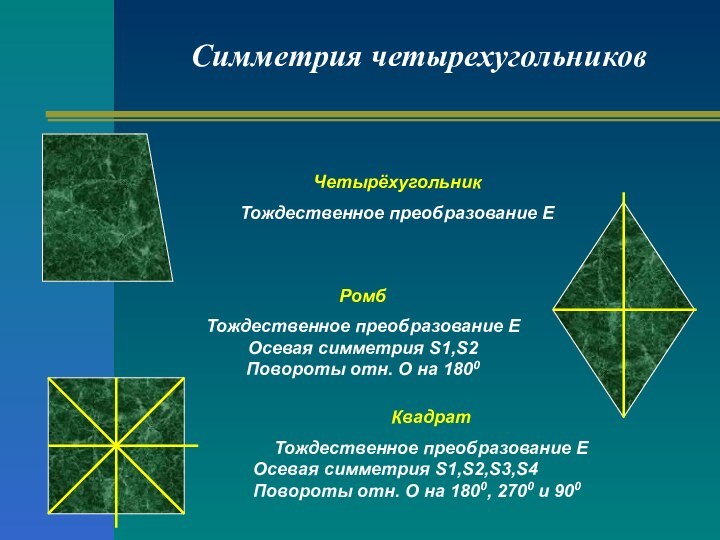
Слайд 23 Симметрия четырехугольников
Четырёхугольник
Тождественное преобразование Е
Ромб
Тождественное преобразование Е
Осевая симметрия S1,S2
Повороты

отн. О на 1800

Квадрат
Тождественное преобразование Е
Осевая симметрия S1,S2,S3,S4
Повороты отн.

О на 1800, 2700 и 900

Слайд 24 Круг и шар
Круг и шар – самые совершенные

из фигур. Эти фигуры обладают бесконечным множеством симметрий.

Слайд 25 Распределение фигур по классам симметрии
Распределение по классам симметрий

Распределение фигур по классам симметрииРаспределение по классам симметрий дает нам новый

дает нам новый взгляд на фигуры. К одному классу

(1) мы отнесем фигуры, которые совмещаются единственным способом, к другому (2) отнесем фигуры, имеющие два и более вида симметрии. К отдельному (3) классу отнесем фигуры, которые обладают бесконечным множеством симметрий.

Слайд 26 Конструируем симметрию сами

Слайд 27 Симметрия танца

Слайд 28 Симметрия и асимметрия
Симметрия и асимметрия - это две

Симметрия и асимметрияСимметрия и асимметрия - это две формы проявления одной

формы проявления одной и той же закономерности - закономерности

двойственности.

Симметрия воспринимается нами как покой, скованность, закономерность, тогда как асимметрия означает движение, свободу, случайность.

Истинную красоту можно постичь только в единстве противоположностей

Москва Храм Христа Спасителя

Болгария София Александроневская лавра

Слайд 29 Примером удивительного сочетания симметрии и асимметрии является Храм

Примером удивительного сочетания симметрии и асимметрии является Храм Василия Блаженного.Это композиция

Василия Блаженного.
Это композиция из 10 храмов, каждый из которых

обладает центральной симметрией, в целом асимметрична. Симметричные архитектурные детали собора как бы кружатся в асимметричном беспорядочном танце вокруг центрального шатра.