Слайд 2
В данной работе рассматривается несколько загадочных и
таинственных историй, которые могли произойти в жизни любого класса
в любой школе.
Но оказывается, что знание законов математики и умение их применить в жизненной ситуации дают нам возможность разгадать эти таинственные истории.
Загадочные истории можно сформулировать как логические задачи и решить их разными способами. Рассмотрим некоторые методы решения логических задач.
Слайд 3
Графический метод.
Графический метод заключается в
следующем: высказывания мы будем изображать точками, а соответствия между
ними будем обозначать отрезками. Эти отрезки называются графами.
Слайд 4
«Однажды Андрей, Борис, Володя, Даша и Галя
договорились пойти в кино. Выбор кинотеатра и фильма они
решили согласовать по телефону. Было также решено, что если с кем-то созвониться не удастся, то поход в кино отменяется.
Вечером у кинотеатра собрались не все, и поэтому посещение кино сорвалось.
а) Таинственная и загадочная история с телефонными звонками:
Слайд 5
На следующий день стали выяснять, кто кому звонил.
Оказалось, что
Андрей звонил Борису и Володе;
Володя звонил Борису и
Даше;
Борис звонил Андрею и Даше;
Даша звонила Андрею и Володе;
Галя звонила Андрей, Володе,Борису.
Как же узнать, кто не созвонился?
Попробуем изобразить эту ситуацию с помощью точек и отрезков, то есть графов.
Слайд 6
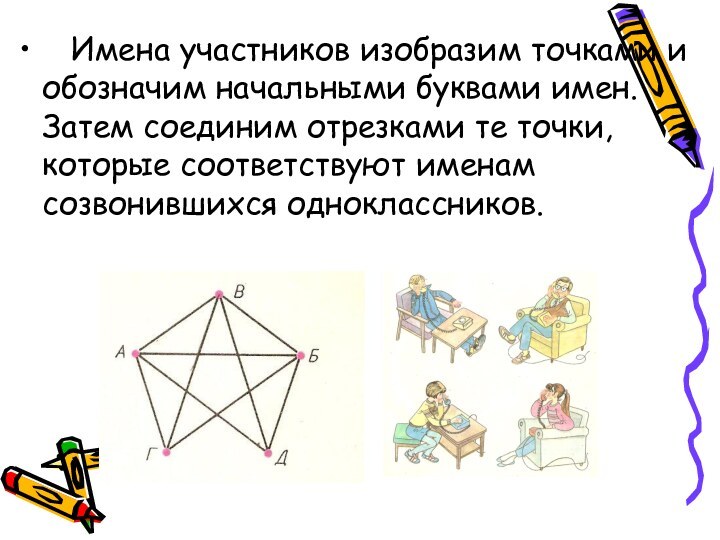
Имена участников изобразим точками и обозначим
начальными буквами имен. Затем соединим отрезками те точки, которые
соответствуют именам созвонившихся одноклассников.
Слайд 7
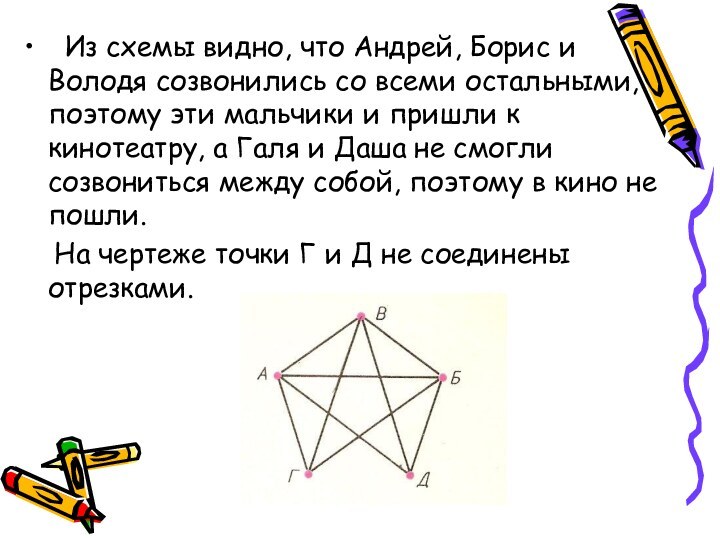
Из схемы видно, что Андрей, Борис и
Володя созвонились со всеми остальными, поэтому эти мальчики и
пришли к кинотеатру, а Галя и Даша не смогли созвониться между собой, поэтому в кино не пошли.
На чертеже точки Г и Д не соединены отрезками.
Слайд 8
б) «Загадочная история с букетом цветов».
Эта история
произошла в день 8 Марта. Кто-то принес букет цветов
и поставил его в вазу на учительском столе. Итак, кто же принес цветы?
Были высказаны предположения:
цветы принесли Андрей и Борис;
цветы принесли Андрей и Даша;
цветы принесли Андрей и Сергей;
цветы принесли Борис и Даша;
цветы принесли Борис и Володя;
цветы принесли Володя и Галя;
цветы принесли Галя и Даша.
Слайд 9
Известно было также, что в одном из
предположений одно имя названо правильно, а второе имя-неправильно. Во
всех остальных предположениях оба имени названы неправильно.
Попробуем и эту загадку решить с помощью графов.
Слайд 10
Решение.
В данной истории приняло участие шесть учеников:
Андрей, Борис, Даша, Сергей, Володя, Галя. Они
образовали следующие пары:
Андрей – Борис,
Андрей – Даша,
Андрей – Сергей,
Борис – Даша,
Борис – Володя,
Володя – Галя,
Галя – Даша.
Слайд 11
Изобразим имена точками и обозначим их буквами
А,Б,В,Г,Д,С.
Каждые два имени из предположений соединим отрезками. Из
всех предположений надо найти то, в котором одно имя верное. Это значит, надо найти отрезок, одному из концов которого соответствует правильное имя, но эта точка не может быть связана с другими точками, так как это имя содержится только в одном предположении. Следовательно на рисунке надо найти точку, которая связана с единственной другой точкой.
На рисунке эта точка обозначена именем Сергей, следовательно цветы принес Сергей.
Слайд 12
Не только графический метод позволяет распутывать загадки.
Рассмотрим второй прием решения логических задач.
Слайд 13
Табличный метод.
В классе проводился классный час
«Знакомство со строительными специальностями.» Мы познакомились с группой строителей.
Их было пять человек: Андреев, Борисов, Иванов, Петров, Сидоров. Профессии у них были разные: маляр, плотник, штукатур, каменщик, электрик. О них было известно следующее:
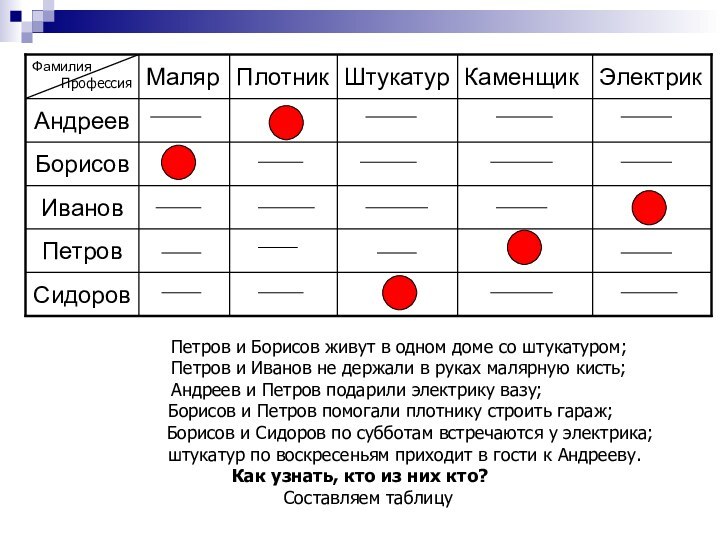
Петров и Борисов живут в одном доме со штукатуром;
Петров и Иванов не держали в руках малярную кисть;
Андреев и Петров подарили электрику вазу;
Борисов и Петров помогали плотнику строить гараж;
Борисов и Сидоров по субботам встречаются у электрика;
штукатур по воскресеньям приходит в гости к Андрееву.
Как узнать, кто из них кто?
Составляем таблицу
Слайд 15
Из первого условия видно, что
Петров и Иванов не маляры, против их фамилий поставим
в графе «Маляр» прочерк;
Из второго условия следует, что Борисов и Петров не штукатуры, значит против этих фамилий также ставим прочерк в графе «Штукатур»
Из третьего условия против фамилий Андреев и Петров в графе «Электрик» прочерк;
Следуя четвертому условию, против фамилий Борисов и Петров в графе «Плотник» ставим прочерк.
Из пятого условия следует, что против фамилий Борисов и Сидоров в графе «Электрик» ставим прочерк.
Из шестого условия против фамилии Андреев ставим прочерк в графе «Штукатур»
Слайд 16
Анализируя таблицу, видим, что в строке «Петров»
только одна свободная клетка «Каменщик», следовательно Петров – каменщик.
Вычеркиваем графу «Каменщик» против других фамилий. В строке «Борисов» одна пустая клетка «Маляр», следовательно Борисов – маляр.
Зачеркиваем клетку «Маляр». В строке «Андреев» пустая клетка «Плотник», следовательно Андреев – плотник.
Рассуждая аналогично, получим
Сидоров – штукатур;
Иванов – электрик.
Такой прием решения логической задачи называется табличным. Рассмотрим ещё задачу, которая решается табличным методом.
Слайд 17
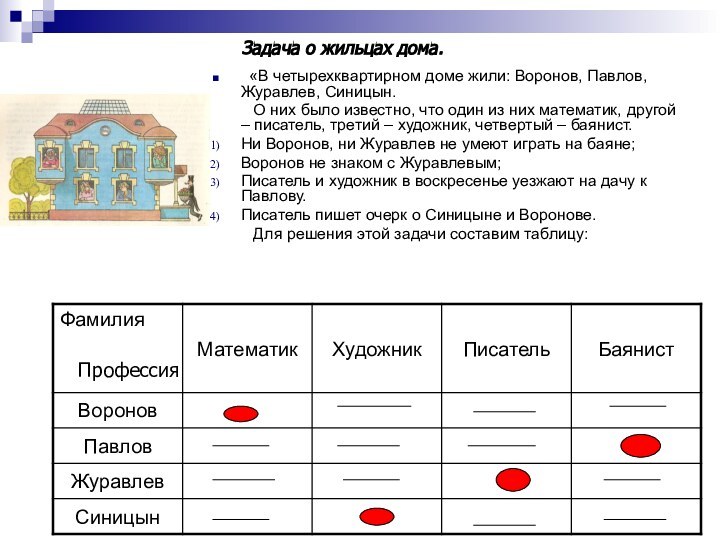
«В четырехквартирном доме жили: Воронов, Павлов, Журавлев,
Синицын.
О них было известно, что один из них математик, другой – писатель, третий – художник, четвертый – баянист.
Ни Воронов, ни Журавлев не умеют играть на баяне;
Воронов не знаком с Журавлевым;
Писатель и художник в воскресенье уезжают на дачу к Павлову.
Писатель пишет очерк о Синицыне и Воронове.
Для решения этой задачи составим таблицу:
Задача о жильцах дома.
Профессия
Слайд 18
Из первого условия следует, что в графе
«баянист» против фамилии Воронов и Журавлев надо поставить прочерк;
Из второго условия следует, что ни Воронов, ни Журавлев не могут быть художником или писателем. Поэтому против фамилий Воронов и Журавлев вычеркиваем «художник», «писатель».
Из третьего условия против фамилии «Павлов» поставим прочерки в клетках «писатель», «художник».
Из четвертого условия следует, что ни Синицын, ни Воронов не могут быть писателями, тогда против их фамилий в графе «писатель» ставим прочерк.
Слайд 19
Теперь видно, что Журавлёв – писатель, и в
соответствующей клетке мы поставим точку.
Вернёмся теперь к условию,
что писатель и художник бывают на даче у Павлова. Но мы узнали, что писатель – это Журавлёв. Значит, на даче встречаются Павлов, Журавлев и художник. Отсюда следует, что художником должен быть либо Воронов, либо Синицын. Допустим, что художник – это Воронов. Тогда на даче встречаются Павлов, Журавлев и Воронов, и, следовательно, Воронов знаком с Журавлёвым. Но в условии задачи сказано, что они не знакомы.
Значит, допущение было неверным. Остаётся второй случай: художник – это Синицын. Поэтому в строке «Синицын» против графы «Художник» ставим точку. Теперь надо вычеркнуть все те строки и столбцы, на пересечении которых стоят точки. После этого сразу будет видно, что Воронов – математик, а Павлов – баянист.
Слайд 20
Итак, используя табличный метод, были установлены профессии жильцов
дома:
Воронов – математик.
Павлов – баянист.
Журавлев – писатель.
Синицын – художник.