- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Множественная регрессия и корреляция
Содержание
- 2. Множественная регрессияЭконометрика - Alexander HollayПарная регрессия может
- 3. Множественная регрессияЭконометрика - Alexander Hollay
- 4. Множественная регрессия. ПрименениеЭконометрика - Alexander HollayМножественная регрессия
- 5. Спецификация модели. Отбор факторов при построенииуравнения множественной регрессииЭконометрика - Alexander Hollay
- 6. Построение уравнения множественной регрессии Эконометрика - Alexander
- 7. Построение уравнения множественной регрессии Эконометрика - Alexander
- 8. Построение уравнения множественной регрессии. Требования к факторам.Эконометрика
- 9. ИнтеркоррелированностьЭконометрика - Alexander HollayВключение в модель факторов
- 10. Построение уравнения множественной регрессии. Коэффициент детерминации. Эконометрика - Alexander Hollay
- 11. Построение уравнения множественной регрессии. Коэффициент детерминации. Эконометрика - Alexander Hollay
- 12. Построение уравнения множественной регрессии. Коэффициент детерминации. Эконометрика
- 13. Построение уравнения множественной регрессии Эконометрика - Alexander
- 14. Построение уравнения множественной регрессии. Эконометрика - Alexander Hollay
- 15. Построение уравнения множественной регрессии. Эконометрика - Alexander
- 16. Построение уравнения множественной регрессии. Подбор переменных.Эконометрика - Alexander Hollay
- 17. Построение уравнения множественной регрессии. Подбор переменных.Эконометрика - Alexander Hollay
- 18. Построение уравнения множественной регрессии. Подбор переменных.Эконометрика -
- 19. Построение уравнения множественной регрессии. Подбор переменных.Эконометрика -
- 20. Построение уравнения множественной регрессии. Матрица парных коэффициентовЭконометрика - Alexander Hollay
- 21. Построение уравнения множественной регрессии. Матрица парных коэффициентовЭконометрика - Alexander Hollay
- 22. Построение уравнения множественной регрессии. Матрица парных коэффициентовЭконометрика
- 23. Построение уравнения множественной регрессии. Матрица парных коэффициентовЭконометрика
- 24. Подходы к преодолению сильной межфакторной корреляции.Эконометрика -
- 25. Подходы к преодолению сильной межфакторной корреляции.Эконометрика - Alexander Hollay
- 26. Подходы к преодолению сильной межфакторной корреляции.Эконометрика - Alexander Hollay
- 27. Отбор факторовЭконометрика - Alexander HollayОтбор факторов, включаемых
- 28. Отбор факторовЭконометрика - Alexander HollayНаиболее широкое применение
- 29. Отбор факторовЭконометрика - Alexander Hollay
- 30. Метод наименьших квадратов (МНК).Свойства оценок на основе МНКЭконометрика - Alexander Hollay
- 31. Виды уравнений множественной регрессииЭконометрика - Alexander HollayВозможны
- 32. Линейная множественная регрессия Эконометрика - Alexander Hollay
- 33. Линейная множественная регрессия Эконометрика - Alexander Hollay
- 34. Линейная множественная регрессия Эконометрика - Alexander Hollay
- 35. Линейная множественная регрессия Эконометрика - Alexander Hollay
- 36. Линейная множественная регрессия Эконометрика - Alexander HollayКак
- 37. Линейная множественная регрессия Эконометрика - Alexander Hollay
- 38. Линейная множественная регрессия Эконометрика - Alexander Hollay
- 39. Линейная множественная регрессия Эконометрика - Alexander Hollay
- 40. Линейная множественная регрессия Эконометрика - Alexander Hollay
- 41. Линейная множественная регрессия Эконометрика - Alexander Hollay
- 42. Линейная множественная регрессия Эконометрика - Alexander Hollay
- 43. Линейная множественная регрессия Эконометрика - Alexander Hollay
- 44. Линейная множественная регрессия Эконометрика - Alexander Hollay
- 45. Линейная множественная регрессия Эконометрика - Alexander Hollay
- 46. Линейная множественная регрессия Эконометрика - Alexander Hollay
- 47. Линейная множественная регрессия Эконометрика - Alexander Hollay
- 48. Линейная множественная регрессия Эконометрика - Alexander Hollay
- 49. Линейная множественная регрессия Эконометрика - Alexander Hollay
- 50. Линейная множественная регрессия Эконометрика - Alexander Hollay
- 51. Линейная множественная регрессия Эконометрика - Alexander Hollay
- 52. Линейная множественная регрессия Эконометрика - Alexander HollayВ
- 53. Линейная множественная регрессия Эконометрика - Alexander Hollay
- 54. Линейная множественная регрессия Эконометрика - Alexander Hollay
- 55. ПримерЭконометрика - Alexander Hollay
- 56. УсловияЭконометрика - Alexander Hollay
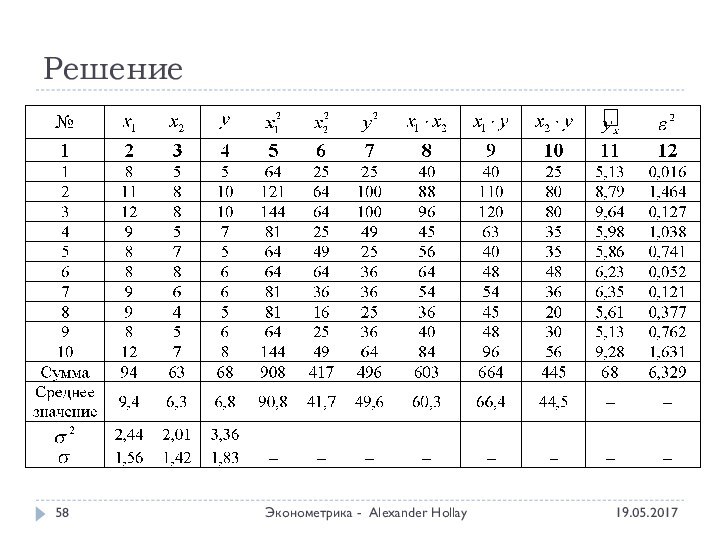
- 57. РешениеЭконометрика - Alexander Hollay
- 58. РешениеЭконометрика - Alexander Hollay
- 59. РешениеЭконометрика - Alexander Hollay
- 60. РешениеЭконометрика - Alexander Hollay
- 61. РешениеЭконометрика - Alexander Hollay
- 62. РешениеЭконометрика - Alexander Hollay
- 63. РешениеЭконометрика - Alexander Hollay
- 64. РешениеЭконометрика - Alexander HollayТак как стандартизованные коэффициенты
- 65. РешениеЭконометрика - Alexander Hollay
- 66. РешениеЭконометрика - Alexander Hollay
- 67. Проверка существенности факторови показатели качества регрессииЭконометрика - Alexander Hollay
- 68. Эконометрика - Alexander HollayПрактическая значимость уравнения множественной
- 69. Показатель множественной корреляцииЭконометрика - Alexander Hollay
- 70. Показатель множественной корреляцииЭконометрика - Alexander Hollay
- 71. Показатель множественной корреляцииЭконометрика - Alexander HollayПри правильном
- 72. Показатель множественной корреляцииЭконометрика - Alexander Hollay
- 73. Показатель множественной корреляцииЭконометрика - Alexander Hollay
- 74. Показатель множественной корреляцииЭконометрика - Alexander HollayФормула индекса
- 75. Показатель множественной корреляцииЭконометрика - Alexander Hollay
- 76. Показатель множественной корреляцииЭконометрика - Alexander Hollay
- 77. Показатель множественной корреляцииЭконометрика - Alexander Hollay
- 78. Показатель множественной корреляцииЭконометрика - Alexander HollayКак видим,
- 79. Показатель множественной корреляцииЭконометрика - Alexander Hollay
- 80. Скорректированный индекс множественной корреляции Эконометрика - Alexander Hollay
- 81. Скорректированный индекс множественной детерминации Эконометрика - Alexander Hollay
- 82. Скорректированный индекс множественной детерминации Эконометрика - Alexander Hollay
- 83. Скорректированный индекс множественной детерминации Эконометрика - Alexander Hollay
- 84. Частные коэффициенты корреляцииЭконометрика - Alexander HollayЧастные коэффициенты
- 85. Частные коэффициенты корреляцииЭконометрика - Alexander Hollay
- 86. Частные коэффициенты корреляцииЭконометрика - Alexander Hollay
- 87. Частные коэффициенты корреляцииЭконометрика - Alexander Hollay
- 88. Частные коэффициенты корреляцииЭконометрика - Alexander Hollay
- 89. Частные коэффициенты корреляцииЭконометрика - Alexander Hollay
- 90. Частные коэффициенты корреляцииЭконометрика - Alexander Hollay
- 91. Частные коэффициенты корреляцииЭконометрика - Alexander Hollay
- 92. Частные коэффициенты корреляцииЭконометрика - Alexander Hollay
- 93. Частные коэффициенты корреляцииЭконометрика - Alexander HollayРассчитанные по
- 94. Частные коэффициенты корреляцииЭконометрика - Alexander Hollay
- 95. Частные коэффициенты корреляцииЭконометрика - Alexander Hollay
- 96. Частные коэффициенты корреляцииЭконометрика - Alexander Hollay
- 97. Частные коэффициенты корреляцииЭконометрика - Alexander Hollay
- 98. Частные коэффициенты корреляцииЭконометрика - Alexander Hollay
- 99. Частные коэффициенты корреляцииЭконометрика - Alexander Hollay
- 100. Оценка значимости уравнения множественной регрессии Эконометрика - Alexander Hollay
- 101. Оценка значимости уравнения множественной регрессии Эконометрика - Alexander Hollay
- 102. Оценка значимости уравнения множественной регрессии Эконометрика - Alexander Hollay
- 103. Оценка значимости уравнения множественной регрессии Эконометрика - Alexander Hollay
- 104. Оценка значимости уравнения множественной регрессии Эконометрика - Alexander Hollay
- 105. Оценка значимости уравнения множественной регрессии Эконометрика - Alexander Hollay
- 106. Оценка значимости уравнения множественной регрессии Эконометрика - Alexander Hollay
- 107. Оценка значимости уравнения множественной регрессии Эконометрика - Alexander Hollay
- 108. Оценка значимости уравнения множественной регрессии Эконометрика - Alexander Hollay
- 109. Оценка значимости уравнения множественной регрессии Эконометрика - Alexander Hollay
- 110. Оценка значимости уравнения множественной регрессии Эконометрика - Alexander Hollay
- 111. Оценка значимости уравнения множественной регрессии Эконометрика - Alexander Hollay
- 112. ПримерЭконометрика - Alexander Hollay
- 113. УсловияЭконометрика - Alexander HollayОценим качество уравнения, полученного в предыдущем разделе.
- 114. РешениеЭконометрика - Alexander Hollay
- 115. РешениеЭконометрика - Alexander Hollay
- 116. РешениеЭконометрика - Alexander Hollay
- 117. РешениеЭконометрика - Alexander Hollay
- 118. РешениеЭконометрика - Alexander Hollay
- 119. РешениеЭконометрика - Alexander Hollay
- 120. РешениеЭконометрика - Alexander Hollay
- 121. РешениеЭконометрика - Alexander Hollay
- 122. РешениеЭконометрика - Alexander Hollay
- 123. РешениеЭконометрика - Alexander Hollay
- 124. РешениеЭконометрика - Alexander Hollay
- 125. Линейные регрессионные моделис гетероскедастичными остаткамиЭконометрика - Alexander Hollay
- 126. Эконометрика - Alexander Hollay
- 127. Эконометрика - Alexander Hollay
- 128. Эконометрика - Alexander Hollay
- 129. НесмещенностьЭконометрика - Alexander HollayНесмещенность оценки означает, что
- 130. ЭффективностьЭконометрика - Alexander HollayОценки считаются эффективными, если
- 131. СостоятельностьЭконометрика - Alexander Hollay
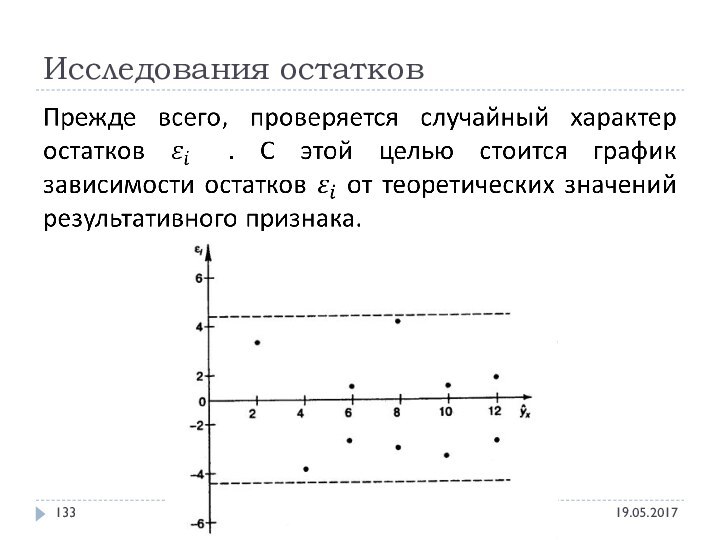
- 132. Исследования остатков Эконометрика - Alexander Hollay
- 133. Исследования остатков Эконометрика - Alexander Hollay
- 134. Исследования остатков Эконометрика - Alexander Hollay
- 135. Исследования остатков Эконометрика - Alexander Hollay
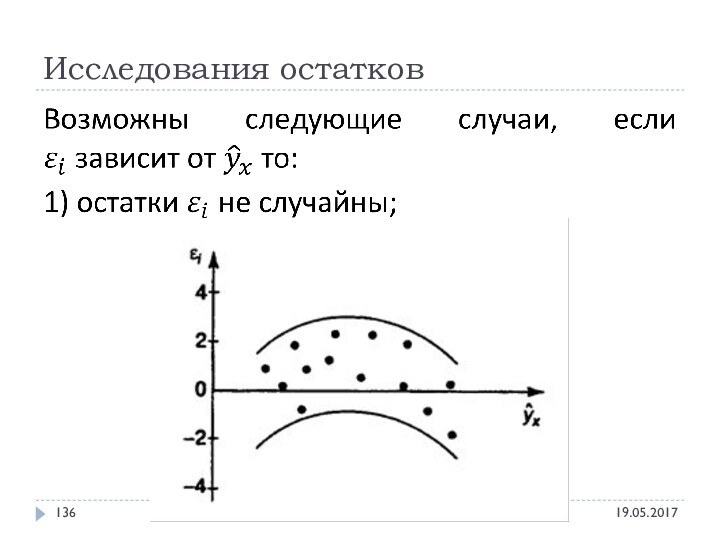
- 136. Исследования остатков Эконометрика - Alexander Hollay
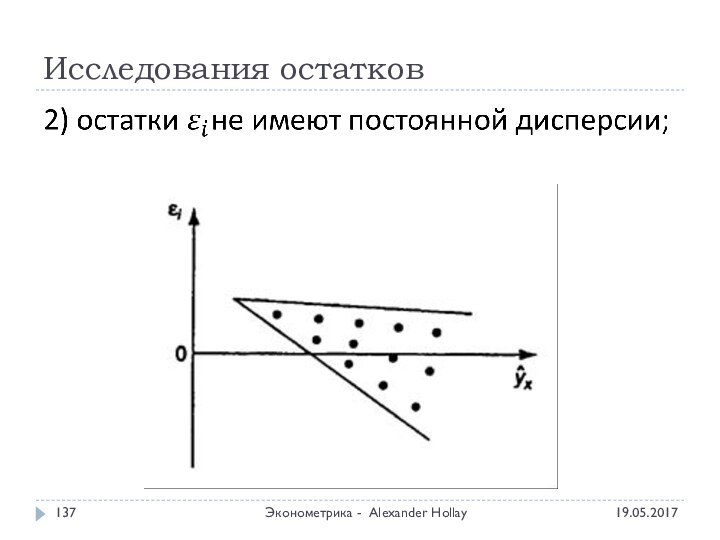
- 137. Исследования остатков Эконометрика - Alexander Hollay
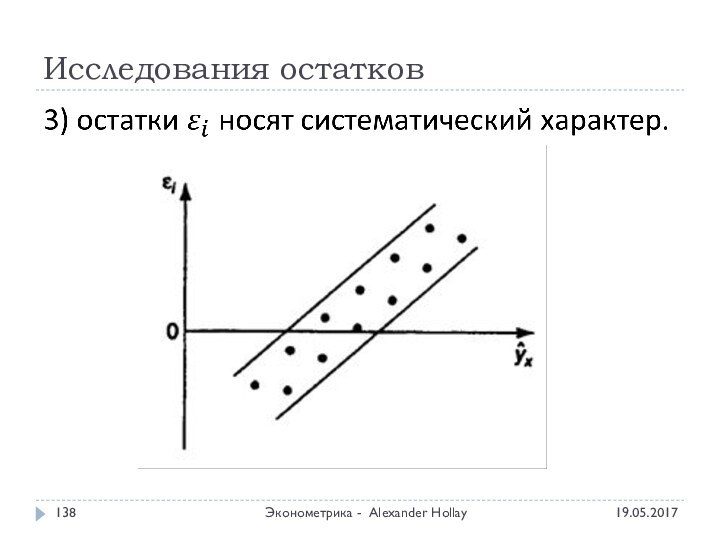
- 138. Исследования остатков Эконометрика - Alexander Hollay
- 139. Исследования остатков Эконометрика - Alexander HollayВ этих
- 140. Исследования остатков Эконометрика - Alexander Hollay
- 141. Исследования остатков Эконометрика - Alexander Hollay
- 142. Исследования остатков Эконометрика - Alexander Hollay
- 143. Исследования остатков Эконометрика - Alexander Hollay
- 144. Исследования остатков Эконометрика - Alexander Hollay
- 145. Исследования остатков Эконометрика - Alexander Hollay
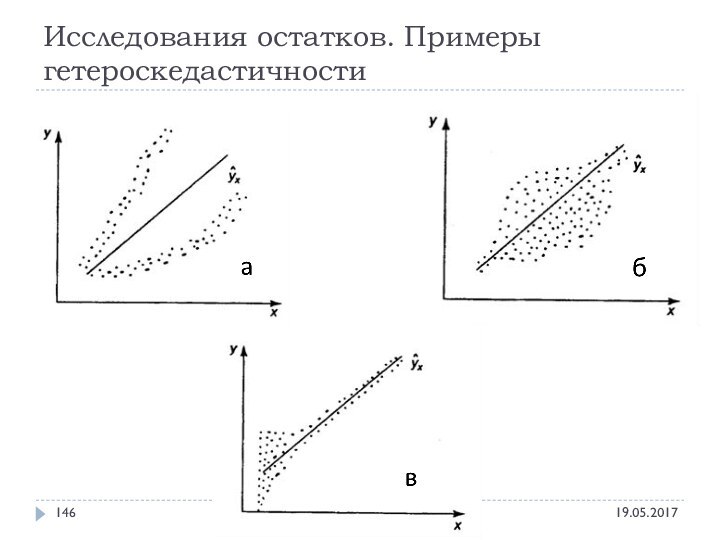
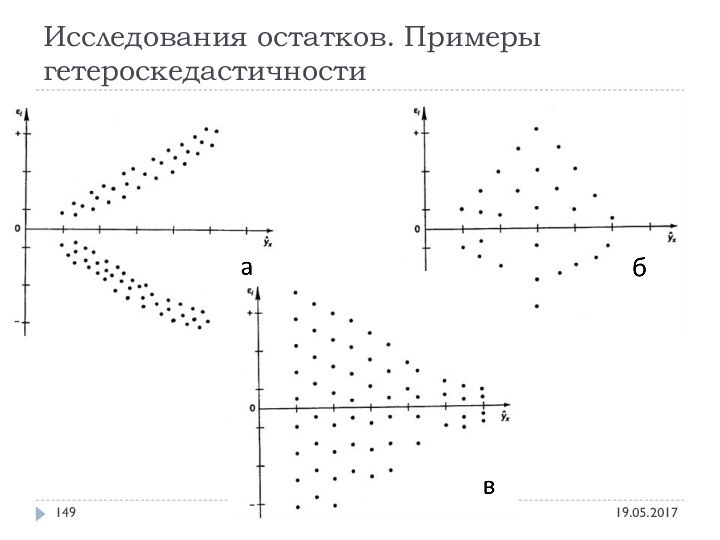
- 146. Исследования остатков. Примеры гетероскедастичности Эконометрика - Alexander Hollay
- 147. Исследования остатков. Примеры гетероскедастичности Эконометрика - Alexander Hollay
- 148. Исследования остатков. Примеры гетероскедастичности Эконометрика - Alexander Hollay
- 149. Исследования остатков. Примеры гетероскедастичности
- 150. Исследования остатков. Эконометрика - Alexander HollayДля множественной
- 151. Исследования остатков. Автокорреляция. Эконометрика - Alexander Hollay
- 152. Исследования остатков. Автокорреляция. Эконометрика - Alexander Hollay
- 153. Исследования остатков. Автокорреляция. Эконометрика - Alexander HollayПри
- 154. Обобщенный метод наименьших квадратов (ОМНК)самостоятельно. См. пособие стр. 73Эконометрика - Alexander Hollay
- 155. Регрессионные модели с переменной структурой(фиктивные переменные)самостоятельно. См. пособие стр. 80Эконометрика - Alexander Hollay
- 156. Скачать презентацию
- 157. Похожие презентации
Множественная регрессияЭконометрика - Alexander HollayПарная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Если же этим влиянием пренебречь нельзя, то в этом случае следует попытаться выявить влияние



















































































































































Слайд 4
Множественная регрессия. Применение
Эконометрика - Alexander Hollay
Множественная регрессия широко
используется в решении проблем спроса, доходности акций, при изучении
функции издержек производства, в макроэкономических расчетах и целом ряде других вопросов эконометрики. В настоящее время множественная регрессия – один из наиболее распространенных методов в эконометрике. Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.
Слайд 5
Спецификация модели. Отбор факторов при построении
уравнения множественной регрессии
Эконометрика
- Alexander Hollay
Слайд 6
Построение уравнения множественной регрессии
Эконометрика - Alexander Hollay
Построение
уравнения множественной регрессии начинается с решения вопроса о спецификации
модели. Он включает в себя два круга вопросов:отбор факторов,
выбор вида уравнения регрессии.
Слайд 7
Построение уравнения множественной регрессии
Эконометрика - Alexander Hollay
Включение
в уравнение множественной регрессии того или иного набора факторов
связано прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями.
Слайд 8
Построение уравнения множественной регрессии. Требования к факторам.
Эконометрика -
Alexander Hollay
Факторы, включаемые во множественную регрессию, должны отвечать следующим
требованиям.1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность.
2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи.
Слайд 9
Интеркоррелированность
Эконометрика - Alexander Hollay
Включение в модель факторов с
высокой интеркорреляцией, может привести к нежелательным последствиям – система
нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии.Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми.
Слайд 10
Построение уравнения множественной регрессии. Коэффициент детерминации.
Эконометрика -
Alexander Hollay
Слайд 11
Построение уравнения множественной регрессии. Коэффициент детерминации.
Эконометрика -
Alexander Hollay
Слайд 12
Построение уравнения множественной регрессии. Коэффициент детерминации.
Эконометрика -
Alexander Hollay
Насыщение модели лишними факторами не только не снижает
величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической незначимости параметров регрессии по критерию Стьюдента.
Слайд 13
Построение уравнения множественной регрессии
Эконометрика - Alexander Hollay
Таким
образом, хотя теоретически регрессионная модель позволяет учесть любое число
факторов, практически в этом нет необходимости. Отбор факторов производится на основе качественного теоретико-экономического анализа. Однако теоретический анализ часто не позволяет однозначно ответить на вопрос о количественной взаимосвязи рассматриваемых признаков и целесообразности включения фактора в модель. Поэтому отбор факторов обычно осуществляется в две стадии: на первой подбираются факторы исходя из сущности проблемы; на второй – на основе матрицы показателей корреляции определяют статистики для параметров регрессии.
Слайд 15
Построение уравнения множественной регрессии.
Эконометрика - Alexander Hollay
Если
факторы явно коллинеарны, то они дублируют друг друга и
один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множественной регрессии как метода исследования комплексного воздействия факторов в условиях их независимости друг от друга.
Слайд 16
Построение уравнения множественной регрессии. Подбор переменных.
Эконометрика - Alexander
Hollay
Слайд 17
Построение уравнения множественной регрессии. Подбор переменных.
Эконометрика - Alexander
Hollay
Слайд 18
Построение уравнения множественной регрессии. Подбор переменных.
Эконометрика - Alexander
Hollay
По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность
факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т.е. имеет место совокупное воздействие факторов друг на друга. Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой и нельзя оценить воздействие каждого фактора в отдельности.
Слайд 19
Построение уравнения множественной регрессии. Подбор переменных.
Эконометрика - Alexander
Hollay
Включение в модель мультиколлинеарных факторов нежелательно в силу следующих
последствий:1. Затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированы; параметры линейной регрессии теряют экономический смысл.
2. Оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования.
Слайд 20
Построение уравнения множественной регрессии. Матрица парных коэффициентов
Эконометрика -
Alexander Hollay
Слайд 21
Построение уравнения множественной регрессии. Матрица парных коэффициентов
Эконометрика -
Alexander Hollay
Слайд 22
Построение уравнения множественной регрессии. Матрица парных коэффициентов
Эконометрика -
Alexander Hollay
Если же, наоборот, между факторами существует полная линейная
зависимость и все коэффициенты корреляции равны единице, то определитель такой матрицы равен нулю:
Слайд 23
Построение уравнения множественной регрессии. Матрица парных коэффициентов
Эконометрика -
Alexander Hollay
Чем ближе к нулю определитель матрицы межфакторной корреляции,
тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
Слайд 24
Подходы к преодолению сильной межфакторной корреляции.
Эконометрика - Alexander
Hollay
Существует ряд подходов преодоления сильной межфакторной корреляции.
Самый простой
путь устранения мультиколлинеарности состоит в исключении из модели одного или нескольких факторов. Другой подход связан с преобразованием факторов, при котором уменьшается корреляция между ними.
Слайд 27
Отбор факторов
Эконометрика - Alexander Hollay
Отбор факторов, включаемых в
регрессию, является одним из важнейших этапов практического использования методов
регрессии. Подходы к отбору факторов на основе показателей корреляции могут быть разные. Они приводят построение уравнения множественной регрессии соответственно к разным методикам. В зависимости от того, какая методика построения уравнения регрессии принята, меняется алгоритм ее решения на ЭВМ.
Слайд 28
Отбор факторов
Эконометрика - Alexander Hollay
Наиболее широкое применение получили
следующие методы построения уравнения множественной регрессии:
1. Метод исключения – отсев
факторов из полного его набора.2. Метод включения – дополнительное введение фактора.
3. Шаговый регрессионный анализ – исключение ранее введенного фактора.
Слайд 30
Метод наименьших квадратов (МНК).
Свойства оценок на основе МНК
Эконометрика
- Alexander Hollay
Слайд 31
Виды уравнений множественной регрессии
Эконометрика - Alexander Hollay
Возможны разные
виды уравнений множественной регрессии:
линейные,
нелинейные.
Ввиду четкой интерпретации параметров наиболее
широко используется линейная функция.
Слайд 36
Линейная множественная регрессия
Эконометрика - Alexander Hollay
Как известно
из курса математического анализа, для того чтобы найти экстремум
функции нескольких переменных, надо вычислить частные производные первого порядка по каждому из параметров и приравнять их к нулю.
Слайд 52
Линейная множественная регрессия
Эконометрика - Alexander Hollay
В отличие
от парной регрессии частные уравнения регрессии характеризуют изолированное влияние
фактора на результат, ибо другие факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии.
Слайд 64
Решение
Эконометрика - Alexander Hollay
Так как стандартизованные коэффициенты регрессии
можно сравнивать между собой, то можно сказать, что мощность
пласта оказывает большее влияние на сменную добычу угля, чем уровень механизации работ.
Слайд 67
Проверка существенности факторов
и показатели качества регрессии
Эконометрика - Alexander
Hollay
Слайд 68
Эконометрика - Alexander Hollay
Практическая значимость уравнения множественной регрессии
оценивается с помощью показателя множественной корреляции и его квадрата
– показателя детерминации.Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком или, иначе, оценивает тесноту совместного влияния факторов на результат.
Слайд 71
Показатель множественной корреляции
Эконометрика - Alexander Hollay
При правильном включении
факторов в регрессионную модель величина индекса множественной корреляции будет
существенно отличаться от индекса корреляции парной зависимости. Если же дополнительно включенные в уравнение множественной регрессии факторы третьестепенны, то индекс множественной корреляции может практически совпадать с индексом парной корреляции (различия в третьем, четвертом знаках). Отсюда ясно, что сравнивая индексы множественной и парной корреляции, можно сделать вывод о целесообразности включения в уравнение регрессии того или иного фактора.
Слайд 74
Показатель множественной корреляции
Эконометрика - Alexander Hollay
Формула индекса множественной
корреляции для линейной регрессии получила название линейного коэффициента множественной
корреляции, или, что то же самое, совокупного коэффициента корреляции.
Слайд 78
Показатель множественной корреляции
Эконометрика - Alexander Hollay
Как видим, величина
множественного коэффициента корреляции зависит не только от корреляции результата
с каждым из факторов, но и от межфакторной корреляции. Рассмотренная формула позволяет определять совокупный коэффициент корреляции, не обращаясь при этом к уравнению множественной регрессии, а используя лишь парные коэффициенты корреляции.
Слайд 84
Частные коэффициенты корреляции
Эконометрика - Alexander Hollay
Частные коэффициенты корреляции
характеризуют тесноту связи между результатом и соответствующим фактором при
элиминировании (устранении влияния) других факторов, включенных в уравнение регрессии.Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель.