Слайд 2
а) извлечение кубического корня
(кубы чисел от 1 до
10)
Последняя цифра куба числа совпадает с числом, возведенным в
куб, для оснований степени 1, 4, 5, 6, 9 и равна разности числа 10 и числа, возведенного в куб, для остальных оснований: 2, 3, 7, 8.
Первую цифру результата извлечения кубического корня находим следующим образом: отбросим последние три цифры задуманного числа и рассмотрим оставшееся число – между кубами каких чисел оно располагается в таблице кубов. Меньшее из них и дает первую цифру искомого числа.
Слайд 3
Пример 1. Требуется извлечь
.
Решение.
Так как последняя
цифра задуманного числа 7 и 10 – 7 = 3, то 3 последняя цифра искомого числа. Отбрасывая три последние цифры задуманного числа, получи число 389; оно располагается в таблице кубов между кубами чисел 7 и 8. Меньшее из этих чисел и есть первая цифра искомого числа.
Ответ: 73.
Слайд 4
Пример 2. Вычислить .
Решение.
Так как последняя цифра подкоренного числа 6, то
и последняя цифра искомого числа 6. Отбрасывая последние три цифры заданного числа, получим 636; это число располагается между кубами 8 и 9. Меньшее – 8.
Ответ: 86
Слайд 5
Для извлечения кубического корня из чисел свыше 1
млн. нужно держать в памяти ( или на «шпаргалке»)
кубы чисел от 11 до 20.
Пример 3. Вычислить
Решение.
Так как последняя цифра задуманного числа 7 и 10 – 7 = 3, то 3 последняя цифра искомого числа. Отбрасывая три последние цифры задуманного числа, получи число 1 860, которое располагается в таблице кубов между кубами чисел 12 и 13. Меньшее из этих чисел (12) и есть первые две цифры искомого числа.
Ответ: 123
Слайд 6
Задание для самостоятельно решения.
Проверь степень собственной виртуозности
в извлечении кубических корней:
1)
2)
Слайд 7
б) извлечение корня пятой степени:
(Пятые степени чисел от
1 до 10)
Подмечаем свойство: последняя цифра пятой степени числа
совпадает с основанием степени.
Первую цифру искомого результата извлечения корня пятой степени находим следующим образом: отбросим последние пять цифр заданной пятой степени числа и рассмотрим оставшееся число – между какими числами в таблице пятых степеней оно располагается. Меньшее из соответствующих оснований степени покажет первую цифру искомого числа.
Слайд 8
Пример 1. Извлечь
Последняя цифра искомого результата 9.
Отбрасываем последние пять цифр заданного числа, остается число 24,
которое располагается в таблице между пятыми степенями чисел 1 и 2. Значит 1 – первая цифра результата.
Ответ: 19
Слайд 9
Пример 2. Вычислить
Последняя цифра результата 5. Отбрасываем
последние пять цифр заданного числа, остается число 97, которое
располагается в таблице между пятыми степенями чисел 2 и 3.
Ответ: 25
Слайд 10
Задание для самостоятельно решения.
Проверь быстроту извлечения корней:
1)
2)
3)
Слайд 11
в) извлечение корня седьмой степени:
(Седьмые степени чисел от
1 до 10)
Подмечаем, что все цифры, на которые могут
оканчиваться седьмые степени, различны. Последняя цифра седьмой степени совпадает с числом, возведенным в седьмую степень, для оснований степени 1, 4, 5, 6, 9 ( как и у кубов) и равна разности числа 10 и числа, возведенного в седьмую степень, для остальных оснований: 2, 3, 7, 8 (то же, как у кубов)
Слайд 12
Пример 1. Извлечь
Решение.
Последняя цифра заданного числа
7; так как 10 – 7 = 3, то
3 – последняя цифра искомого числа. Найдем первую цифру корня: зачеркиваем последние семь цифр заданного числа, останется число 340, которое располагается в таблице между седьмыми степенями чисел 2 и 3. Меньшее из них (2) дает первую цифру искомого числа.
Ответ: 23.
Слайд 13
Вычислить быстро
Пример 2.
Решение.
Последняя цифра искомого корня
4. Отбросим последние семь цифр заданного числа, останется число
133 892, которое располагается в таблице между седьмыми степенями чисел 5 и 6. Меньшее – 5.
Ответ: 54
Пример 3.
Решение.
Последняя цифра искомого корня 9. Первую цифру находим по числу 9 320 653 из таблицы: 9.
Ответ: 99
Слайд 14
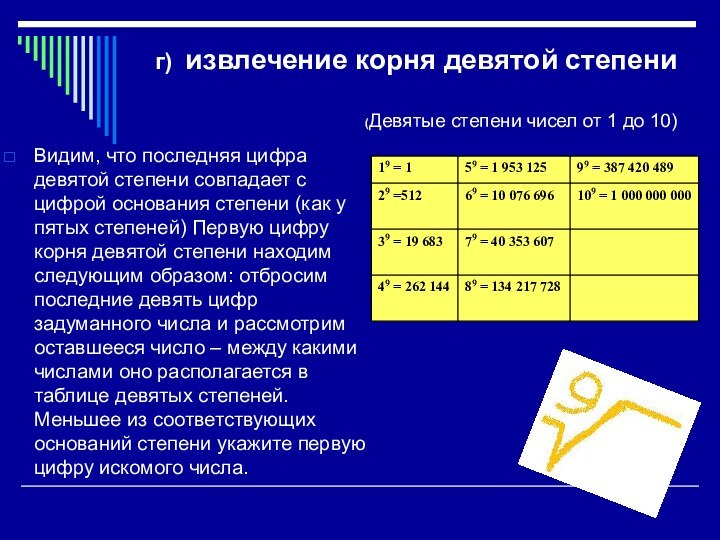
г) извлечение корня девятой степени
(Девятые степени чисел от
1 до 10)
Видим, что последняя цифра девятой степени совпадает
с цифрой основания степени (как у пятых степеней) Первую цифру корня девятой степени находим следующим образом: отбросим последние девять цифр задуманного числа и рассмотрим оставшееся число – между какими числами оно располагается в таблице девятых степеней. Меньшее из соответствующих оснований степени укажите первую цифру искомого числа.
Слайд 15
Вычислить быстро
Пример 1:
Решение. Последняя цифра искомого
числа 3. Первая цифра 3, так как число 46 411
располагается в таблице между девятыми степенями чисел 3 и 4.
Ответ: 33.
Пример 2:
Решение. Последняя цифра – 9, и первая – 9.
Ответ: 99.
Слайд 16
ВИРТУОЗНОЕ ИЗВЛЕЧЕНИЕ КОРНЕЙ ВЫСОКИХ СТЕПЕНЕЙ.
Каждому доступно быстро и
точно или грубо-приближенное извлечение корня высокой степени (m) из
целого числа с большим количеством (n)
цифр. Способ прост: надо отношение считать
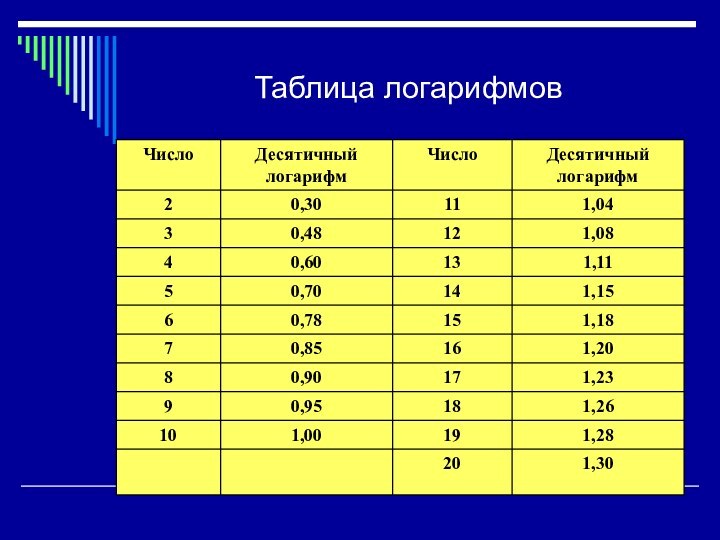
логарифмом искомого числа и по таблице
логарифмов найти его. Если , то практически
достаточна следующая таблица десятичных логарифмов:
Слайд 18
Вычислить
Пример 1.
Решение. Количество цифр (25)числа делим
на показатель корня (51), получаем 0,49. это число находится
в таблице между 0,48 и 0,60. Более близким значением является 0,48. Это lg 3. Значит искомое число 3.
Ответ: 3
Пример 2.
Извлечь корень 65 – ой степени из 20- значного числа 36 893 488 147 419 103 232.
Решение.
Делим 20 на 65, получается 0,31≈ lg2.
Ответ: искомое число 2.
Слайд 19
Извлечь корень 32 – й степени из 38
– значного числа
43 144 141 785 116 080 641 825 668 495 361 328 125.
Решение. Делим 38 на 32,
получаемся приблизительно 1,187. В таблице логарифмов 1,18 < 1,187 < 1,2. Берем меньшее значение логарифма – 1,18; ему соответствует число 15.
Ответ: искомое число 15.
Пример 3.
Слайд 20
Пример 4.
Решение.
Вычислить приближенно ,
где k – 49-значное число. Решаем: 49:47≈1,043. В таблице
логарифмов 1,04 < 1,043 < 1,08. Берем значение 1,04, которому соответствует число 11
Ответ: искомое число ≈11.