Основоположник
теории множеств немецкий математикГеорг Кантор
(1845-1918)
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Множество и его элементы
Содержание
- 3. «Множество есть многое, мыслимое нами как единое».
- 5. Понятие множества принадлежит к числу основных, неопределяемых
- 8. Язык теории множеств
- 9. Элементы множества можно перечислять в произвольном порядке.
- 10. способы задания множествМножество всех чисел, которые больше
- 11. Задание множества с помощью характеристического свойства {х│2 < х
- 12. Элемент х принадлежит множеству Ах является элементом
- 14. ПодмножестваЭлементы, образующие данное множество А, можно объединять
- 15. Определение: Если каждый элемент множества В является
- 16. 2. А = { 2, 4, 6,
- 17. №531(а, б) Множество задано словесным описанием. Задайте
- 18. № 532 (а, в, г)Множество задано перечислением
- 19. № 536(а) Верно ли, что: 0,7
- 20. № 541На числовой прямой изобразите следующие промежутки:А
- 21. Изображение множеств в виде плоских фигур очень
- 22. Круги ЭйлераКруги Эйлера – это особые чертежи,
- 23. Определение: Пересечением множеств А и В называют
- 24. Найти пересечение А∩В множеств А и В.
- 25. Решение систем уравнений, систем неравенств – это
- 26. Определение: Объединением множеств А и В называют
- 27. Найти объединение АUВ множеств А и В.а)
- 28. № 542(а, в) Найдите пересечение А∩В множеств
- 29. № 543 - 544(а, г)Даны числовые промежутки:
- 30. Скачать презентацию
- 31. Похожие презентации
«Множество есть многое, мыслимое нами как единое». Основоположник
Слайд 5 Понятие множества принадлежит к числу основных, неопределяемых понятий
математики. Множество – набор, совокупность, собрание каких-либо объектов (элементов),
обладающих общим для всех их характеристическим свойством. Примеры множеств: множество учащихся в данной аудитории; множество людей, живущих на нашей планете в данный момент времени; множество точек данной геометрической фигуры; множество чётных чисел; множество корней уравнения х2-5х+6=0; множество действительных корней уравнения х2+9=0;
Слайд 8
Язык теории множеств
Множество
состоит из элементов.
{-13;3}
Множество состоит из чисел 3 и
-13Корни уравнения
Х2 + 10х = 39
{А,Е,Е,И,О,У,Ы,Э,Ю,Я}
Множество состоит из букв А,Е,Е,И,О,У,Ы,Э,Ю,Я,
Гласные буквы русского алфавита
{0,1,2,3,4,5,6,
7,8,9}
Множество состоит из цифр 0,1,2,3,4,5,6,7,8,9
Цифры десятичной системы счисления
Задание множества перечислением его элементов
Поэлементное описание множества
Словесное описание множества
Слайд 9 Элементы множества можно перечислять в произвольном порядке. От
изменения порядка перечисления элементов само множество не меняется.
Для числовых
множеств применяют перечисление от меньшего числа к большему числу.Пустое множество т.е. множество, не содержащее ни одного элемента.
Обозначается Ø
Слайд 10
способы задания множеств
Множество всех чисел, которые больше 2
и меньше 7
(2; 7)6
Множество всех чисел, которые больше 2 и меньше 7
{х│2 < х < 7}
5
Множество рациональных чисел
Q
4
Множество натуральных чисел
N
3
Множество всех квадратов натуральных чисел
{1,4, 9,16 25,49, ...}
2
Множество всех двузначных чисел, кратных пяти
{10,15,20, ..., 90,95}
1
Словесное описание множества
Задание множества
Слайд 11
Задание множества с помощью характеристического свойства
{х│2
х
< 7{х│2< х <7}
Множество всех х таких, что ...
{х│...}
Множество всех х ...
{х...}
Множество ...
{ ...}
Как они читаются
Символы
Слайд 12
Элемент х принадлежит множеству А
х является элементом множества
А
Элемент х не
принадлежит множеству Ах не является элементом множества А
Словесные обороты
Слайд 14
Подмножества
Элементы, образующие данное множество А, можно объединять не
сразу все вместе, а группируя их в разных комбинациях.
Так можно получать подмножества данного множества.Пример: А – множество всех учеников девятого класса
В – множество девочек этого девятого класса
С – множество мальчиков этого девятого
класса
В и С – подмножества множества А
Слайд 15 Определение: Если каждый элемент множества В является элементом
множества А, то множество В называют подмножеством множества А.
Обозначение
Знак называют знаком включения
Слайд 17 №531(а, б) Множество задано словесным описанием. Задайте это
множество, перечислив его элементы: а) цифры, которые больше
; б) целые отрицательные числа, которые больше - .задания
Слайд 18
№ 532 (а, в, г)
Множество задано перечислением своих
элементов. Приведите какое-нибудь его словесное описание:
а) {0, 2, 4,
6, 8}в) {3, 6, 9, ..., 27, 30}
г) {A, B, C, D, X, Y, Z}
Слайд 19 № 536(а) Верно ли, что: 0,7 {х│х2 -
1< 0}
№ 538 Дано множество { -8,1; √2; 17/7}.
Перечислите все его подмножества, состоящие из двух чисел:а)разного знака
б)положительных
в)рациональных
г)среди которых есть иррациональное число
Слайд 20
№ 541
На числовой прямой изобразите следующие промежутки:
А =
(-√2; 1), В = [0; 1,9), С = [-1,5;
200/101].Верно ли, что:
а) б)
с) г)
Слайд 21 Изображение множеств в виде плоских фигур очень удобно
для наглядного объяснения различных операций над множествами. Обычно множества изображают
в виде кругов. Такие круги называют кругами Эйлера.
Слайд 22
Круги Эйлера
Круги Эйлера – это особые чертежи, при
помощи которых наглядно представляют отношения между множествами.
Множества А
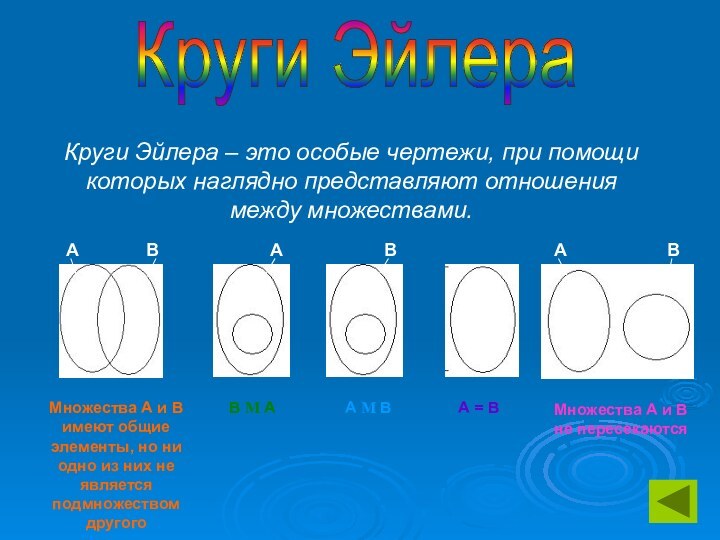
и В имеют общие элементы, но ни одно из них не является подмножеством другого В М А
А М В
А = В
Множества А и В не пересекаются
А
В
А
А
А
В
В
В
А=В
В
Слайд 23 Определение: Пересечением множеств А и В называют множество,
состоящее из всех общих элементов множеств А и В,
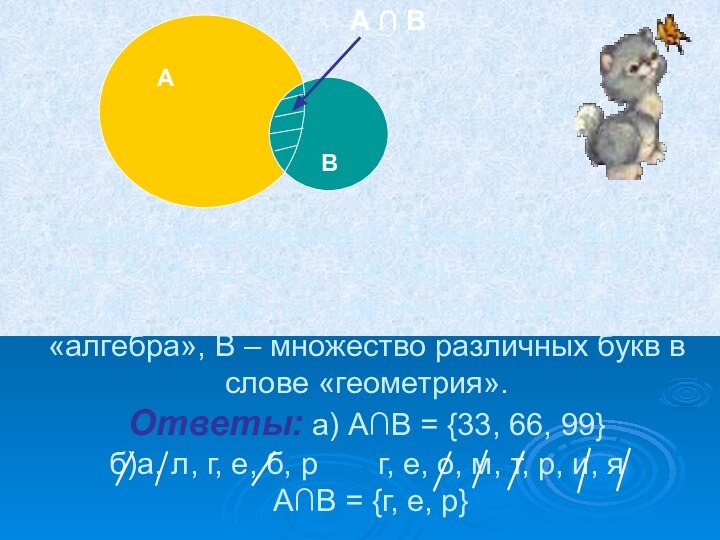
т.е. из всех элементов, которые принадлежат и множеству А, и множеству ВОбозначение: А ∩ В
Запись: А ∩ В = {х│х А и х В }
Слайд 24 Найти пересечение А∩В множеств А и В. а) А
= {11, 22, 33, ..., 88, 99}, В =
{3, 6, 9, ...} б) А – множество различных букв в слове «алгебра», В – множество различных букв в слове «геометрия». Ответы: а) А∩В = {33, 66, 99} б)а, л, г, е, б, р г, е, о, м, т, р, и, я А∩В = {г, е, р}А
В
А ∩ В
Слайд 25 Решение систем уравнений, систем неравенств – это примеры
пересечений различных множеств.
f(x) = 0
g(x) = 0
f(x) >0
g(x)
>0Слайд 26 Определение: Объединением множеств А и В называют множество,
состоящее из всех элементов, которые принадлежат хотя бы одному
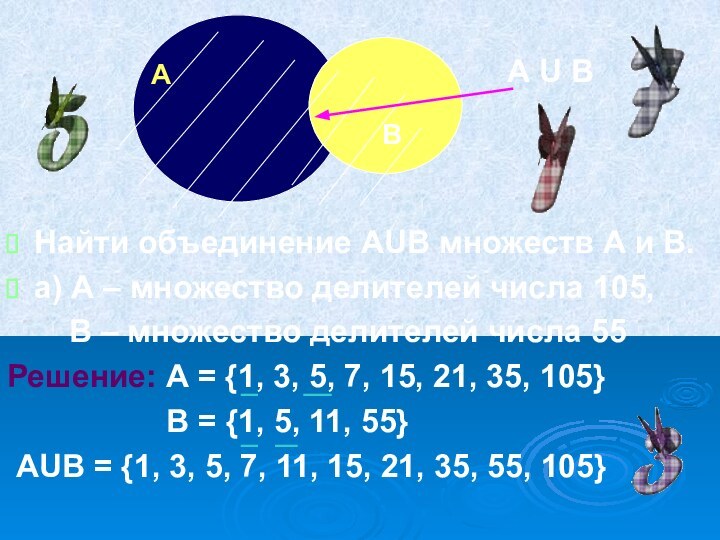
из этих множеств – или множеству А, или множеству В.Обозначение: А U В
Запись: АUВ = {х│х А или х В}
Слайд 27
Найти объединение АUВ множеств А и В.
а) А
– множество делителей числа 105,
В
– множество делителей числа 55Решение: А = {1, 3, 5, 7, 15, 21, 35, 105}
В = {1, 5, 11, 55}
АUВ = {1, 3, 5, 7, 11, 15, 21, 35, 55, 105}
А
В
А U В
Слайд 28 № 542(а, в) Найдите пересечение А∩В множеств А и
В. а)А = {10,20,30, ...}, В = {1 2,3, ...,41} в)А
= {-11,-10,-9, ...,-1,0,1,...9}, В – целые числа, кратные 10.Задания
Слайд 29
№ 543 - 544(а, г)
Даны числовые промежутки:
А
= (0; 1), В = [-0,5; 0,9], С =
[-1; 1],D = (0,1; 1,1]. Изобразите на числовой прямой множества:
а)А ∩ В; г)А ∩ В ∩ С ∩ D
а)А U В; г)А U ВU С U D
