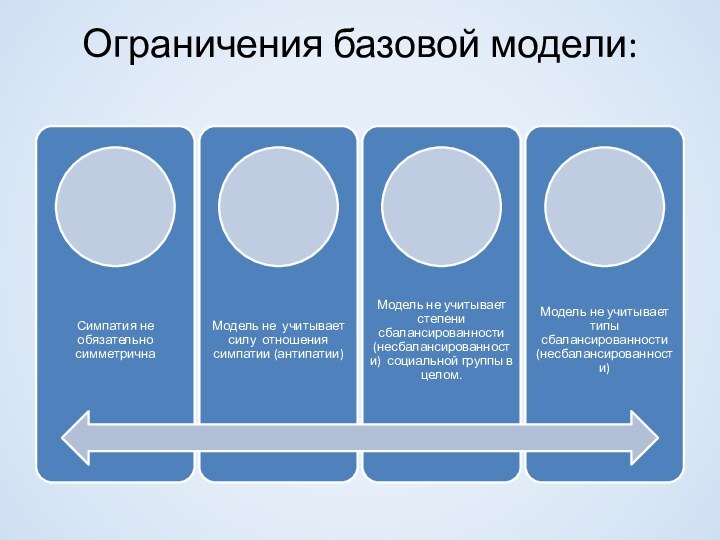
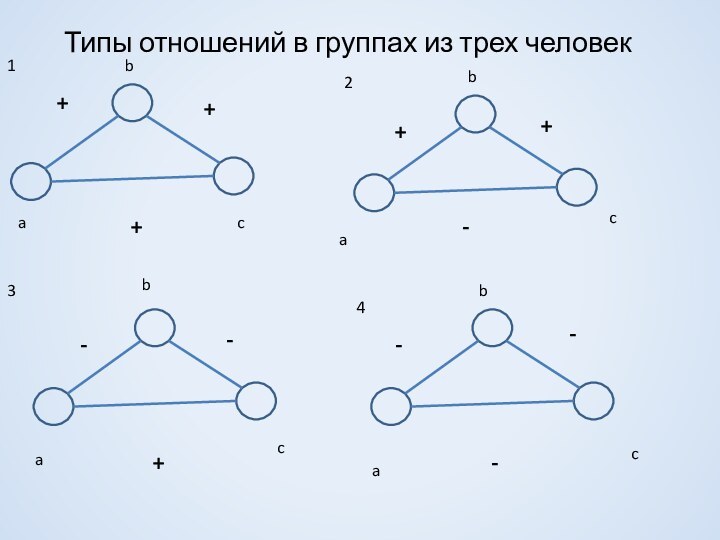
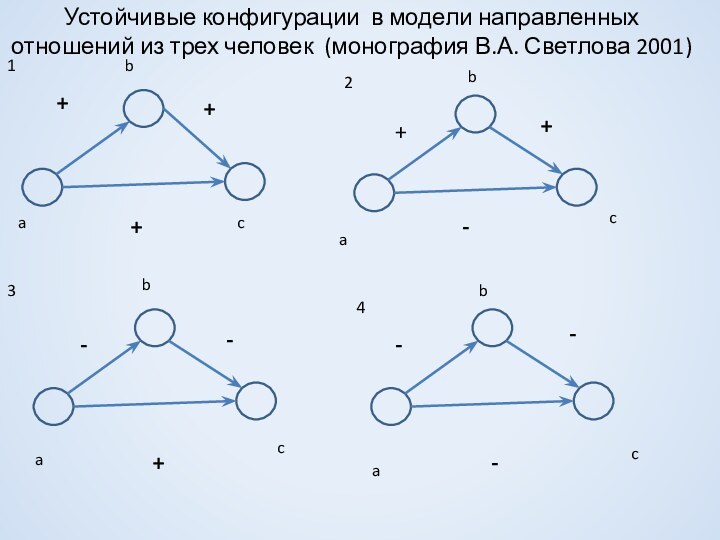
более одного раза
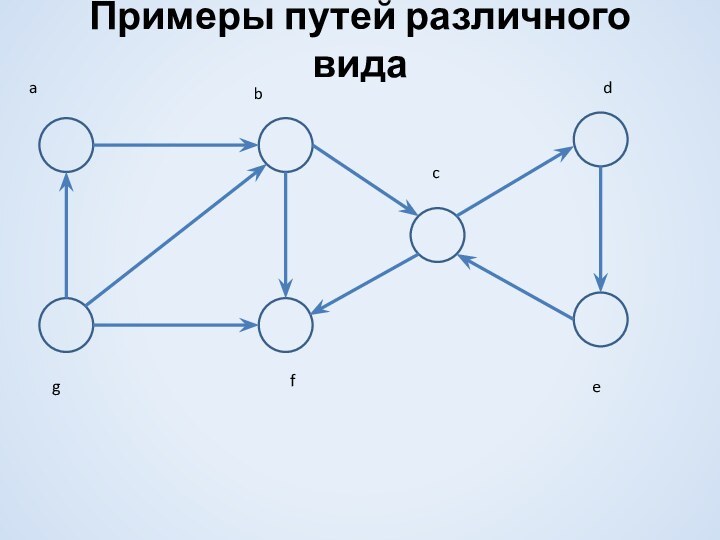
замкнутым, если vt+1 = v1
полным, если содержит
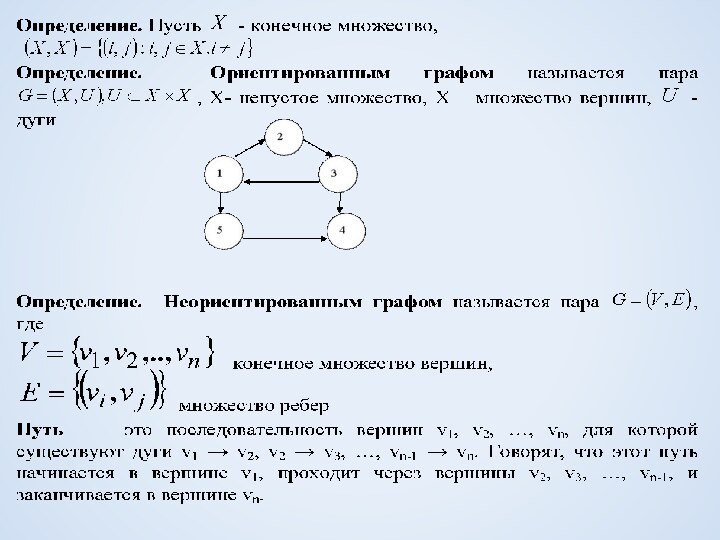
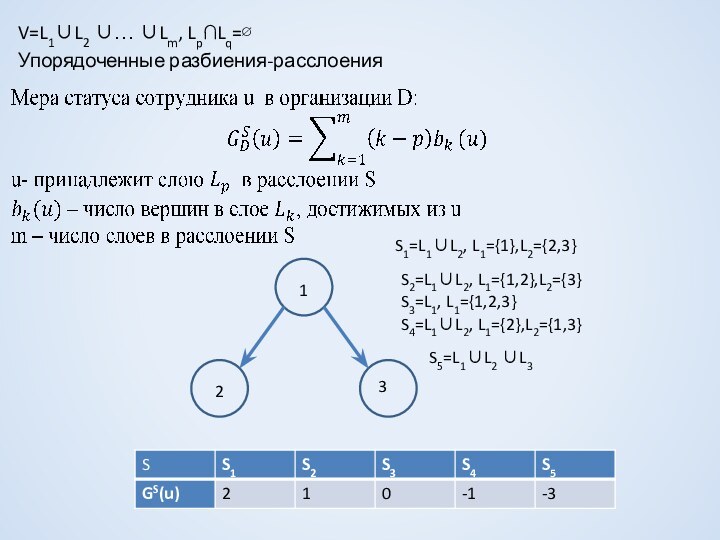
все вершины из VКонтур- простой замкнутый путь в орграфе.
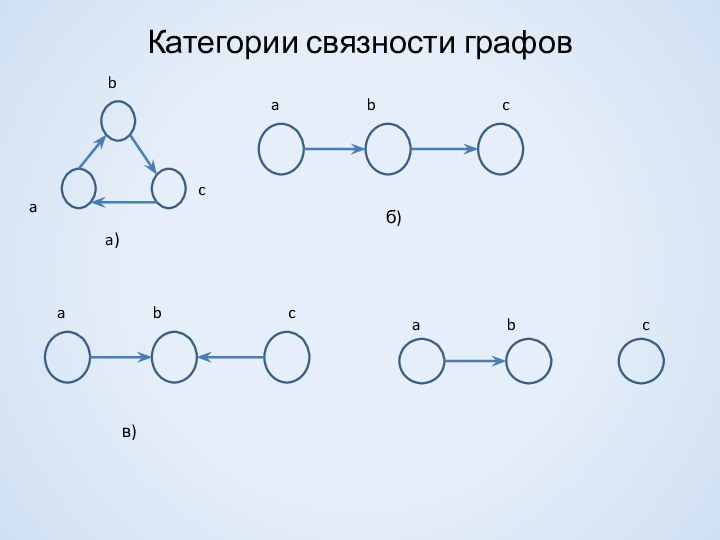
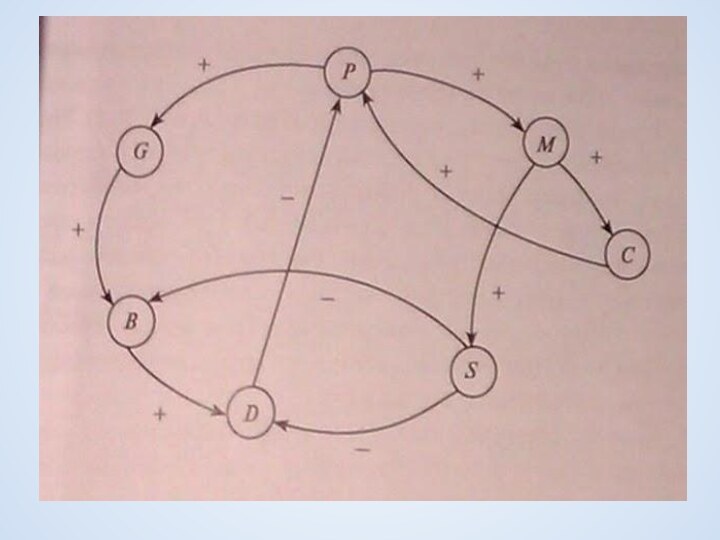
Вершина v достижима из вершины u, если существует путь из u в v (u→v).
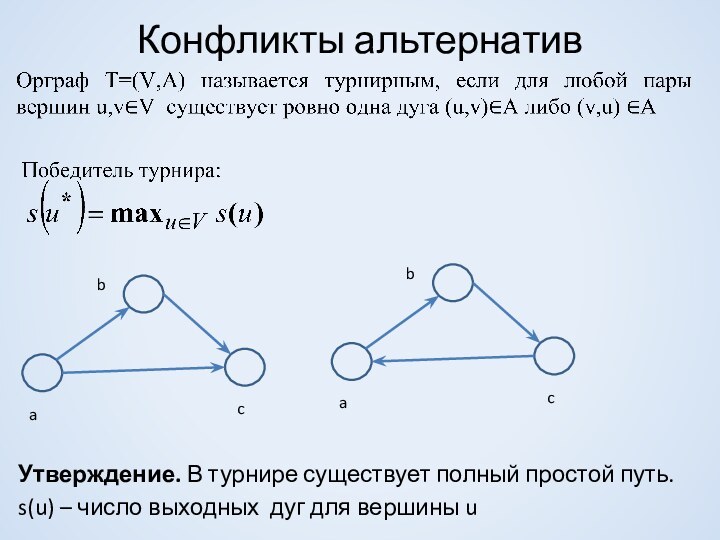
Утверждение. Если u→v, то существует простой путь из u в v .
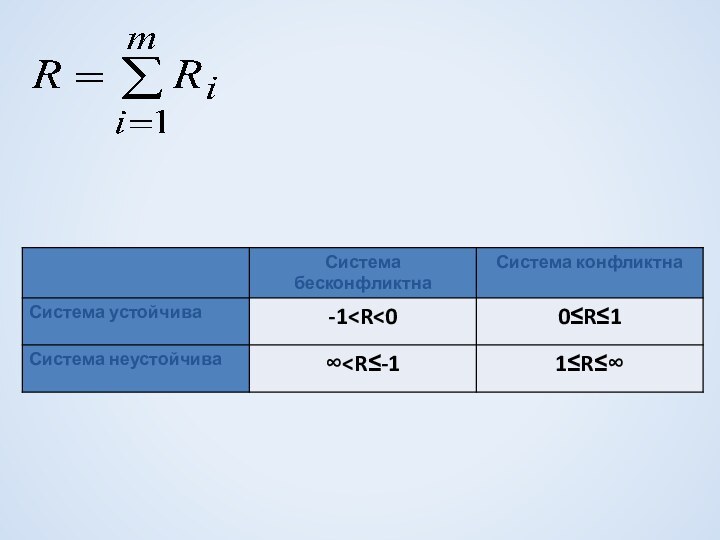
Расстояние между u и v - длина кратчайшего пути (ρ(u,v))
Вершины соединимы, если существует полупуть из u в v (u→v).
Полупуть в орграфе G=(V,A) – последовательность вершин и дуг v1, а1, v2, а2 , vt, аt , vt+1
ai – (vi ,vi+1 ) или (vi+1 , vi)