Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть

Презентация на тему Моделирование потребительского поведения и спроса

Содержание

2. Аксиомы1)Ненасыщаемость2)Совершенность3)Транзитивность4)Рефлексивность
3. Ненасыщаемость. Больший набор всегда предпочитается меньшему. Если , то
4. Совершенность. В отношении двух наборов и
5. Это означает, что не существует таких наборов, которые потребитель не мог бы сравнить с другими.
6. После упорядочения отношений потребителя к отдельным наборам
7. ПолезностьВ теории полезности понятие полезность означает не
8. Функция полезностиявляется индикатором предпочтения, поскольку она обладает следующим характеристическим свойством: тогда и только тогда, когда
9. рассматривается как некоторая монотонно возрастающая функция, определенная на множестве потребительских наборов
10. Геометрическим образом функции полезности является гиперповерхность в
11. Чаще всего применяются- линейная, -квадратичная -логарифмическая функции
12. В качестве примера приведем конкретную квадратичную функцию
14. Свойства функции полезности1. С ростом потребления любого
15. 2. Небольшой прирост блага при его первоначальном отсутствии резко увеличивает полезность
16. 3. Предельная полезность каждого блага уменьшается, если
17. 4. При очень большом объеме блага его дальнейшее увеличение не приводит к увеличению полезности
18. 5. Предельная полезность каждого блага увеличивается,
19. Здесь благо, количество которого фиксировано, оказывается относительно
20. Графический анализ функции полезности. Линии уровня. Рассмотрим
21. Кривые безразличия.Для функции полезности линии уровня называют
22. Типы кривых безразличия.Линейная. Функция полезности с полным
23. Неоклассическая (степенная)функция полезности , где α+β
24. С полным взаимодополнением благ (например, при увеличении
25. Кривые безразличия для функции полезности с полным взаимодополнением благ
26. Свойства кривых безразличияНа основании аксиомы поведения потребителя
27. Кривые безразличия никогда не пересекаются, т.к. через
28. Кривые безразличия имеют отрицательный наклон. Абсолютный наклон
29. Предельная норма замещения благ.Выражение называют предельной нормой
30. В общем виде формулу предельной нормы замещения
31. Для определения поведения потребителя, нужны ещё сведения
32. Бюджетным множеством называется множество всех наборов благ,
33. Бюджетной линией называется геометрическое место точек всех комбинаций благ, стоимость которых равна определённой сумме.
34. При постоянных ценах на оба блага, линия
35. Задача о максимальном выборе потребителя.При заданных ценах
36. Такая точка называется точкой равновесия. В точке
37. Задача о максимальном выборе потребителя сводится к
38. Решение этой задачи на условный экстремум находят
39. при или
40. Решая систему, получаем набор благ оптимизирующий полезность
41. При этом оптимальное значение множителя Лагранжа называется
42. Скачать презентацию
43. Похожие презентации

Аксиомы1)Ненасыщаемость2)Совершенность3)Транзитивность4)Рефлексивность

Главная
Математика
Моделирование потребительского поведения и спроса

Кафедра математики и моделированияСтарший преподаватель Е.Г. ГусевКурс «Высшая математика»Лекция 22. Тема: Моделирование

Аксиомы1)Ненасыщаемость2)Совершенность3)Транзитивность4)Рефлексивность

Ненасыщаемость. Больший набор всегда предпочитается меньшему. Если , то

Совершенность. В отношении двух наборов и

Это означает, что не существует таких наборов, которые потребитель не мог бы сравнить с другими.

После упорядочения отношений потребителя к отдельным наборам благ строится функция предпочтений или

ПолезностьВ теории полезности понятие полезность означает не что иное как порядок предпочтения.

Функция полезностиявляется индикатором предпочтения, поскольку она обладает следующим характеристическим свойством: тогда и только тогда, когда

рассматривается как некоторая монотонно возрастающая функция, определенная на множестве потребительских наборов

Геометрическим образом функции полезности является гиперповерхность в n+1 – мерном пространстве, где

Чаще всего применяются- линейная, -квадратичная -логарифмическая функции вида

В качестве примера приведем конкретную квадратичную функцию полезности для трех агрегированных групп

Моделирование потребительского поведения и спроса

Свойства функции полезности1. С ростом потребления любого блага полезность растет. Частные производные

2. Небольшой прирост блага при его первоначальном отсутствии резко увеличивает полезность

3. Предельная полезность каждого блага уменьшается, если объем его потребления растет, то

4. При очень большом объеме блага его дальнейшее увеличение не приводит к увеличению полезности

5. Предельная полезность каждого блага увеличивается, если растет количество другого блага.

Здесь благо, количество которого фиксировано, оказывается относительно дефицитным, поэтому дополнительная его единица

Графический анализ функции полезности. Линии уровня. Рассмотрим функцию полезности U=U(x1,x2). Линией уровня

Кривые безразличия.Для функции полезности линии уровня называют линиями или кривыми безразличия. Линия

Типы кривых безразличия.Линейная. Функция полезности с полным взаимозамещением благ имеет вид U=ax1+bx2,

Неоклассическая (степенная)функция полезности , где α+β

С полным взаимодополнением благ (например, при увеличении спроса на одно благо, растёт

Кривые безразличия для функции полезности с полным взаимодополнением благ

Свойства кривых безразличияНа основании аксиомы поведения потребителя кривая безразличия, лежащая выше и

Кривые безразличия никогда не пересекаются, т.к. через любую точку на карте можно

Кривые безразличия имеют отрицательный наклон. Абсолютный наклон кривой безразличия при движении вправо

Предельная норма замещения благ.Выражение называют предельной нормой замещения первого блага вторым, которая

В общем виде формулу предельной нормы замещения благ записывают в виде которая

Для определения поведения потребителя, нужны ещё сведения о доходе потребителя и рыночных

Бюджетным множеством называется множество всех наборов благ, которые может приобрести потребитель, имея

Бюджетной линией называется геометрическое место точек всех комбинаций благ, стоимость которых равна определённой сумме.

При постоянных ценах на оба блага, линия цен - это прямая линия,

Задача о максимальном выборе потребителя.При заданных ценах и имеющемся доходе потребитель стремится

Такая точка называется точкой равновесия. В точке равновесия наклон бюджетной линии и

Задача о максимальном выборе потребителя сводится к отысканию точки равновесия. Требуется найти

Решение этой задачи на условный экстремум находят с помощью метода множителей Лагранжа.

Решая систему, получаем набор благ оптимизирующий полезность и при котором все предельные

При этом оптимальное значение множителя Лагранжа называется предельной полезностью денег, которая показывает

Вопросы:1)Дать понятие полезности, функции полезности.2)В чем заключается задача об оптимальном выборе потребителя?

Слайды презентации

Слайд 2 Аксиомы
1)Ненасыщаемость
2)Совершенность
3)Транзитивность
4)Рефлексивность

Слайд 3 Ненасыщаемость.
Больший набор всегда предпочитается меньшему. Если

, то

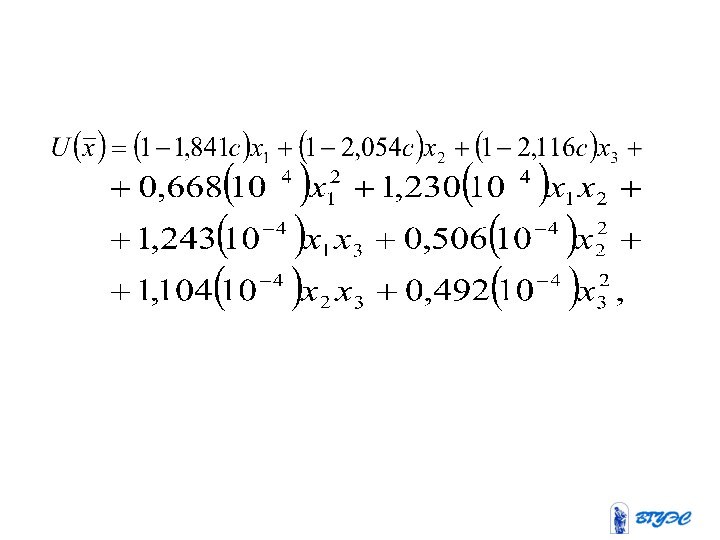
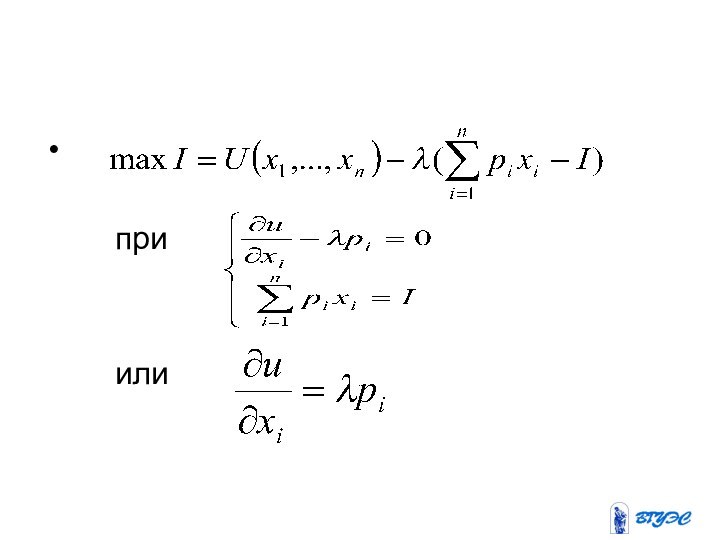
Слайд 4 Совершенность.

В отношении двух наборов и

потребитель может однозначно определить, предпочитает он набор набору , набор предпочитает, или они для него равнозначны (эквивалентны).

Слайд 5 Это означает, что не существует таких наборов, которые

потребитель не мог бы сравнить с другими.

Слайд 6 После упорядочения отношений потребителя к отдельным наборам благ

После упорядочения отношений потребителя к отдельным наборам благ строится функция предпочтений

строится функция предпочтений или функция порядковой полезности. Другими словами,

на множестве потребительских наборов определяют функцию полезности

потребителя.

Слайд 7 Полезность
В теории полезности понятие полезность означает не что

ПолезностьВ теории полезности понятие полезность означает не что иное как порядок

иное как порядок предпочтения. Потребитель выбирает предпочтительный набор благ

из всех доступных для него.

Слайд 8 Функция полезности
является индикатором предпочтения, поскольку она обладает следующим

характеристическим свойством:

тогда и только тогда, когда

Слайд 9 рассматривается как некоторая монотонно возрастающая функция, определенная

на множестве потребительских наборов

Слайд 10 Геометрическим образом функции полезности является гиперповерхность в n+1

Геометрическим образом функции полезности является гиперповерхность в n+1 – мерном пространстве,

– мерном пространстве, где n измерений образуют блага, n+1

измерение характеризует полезность каждого из соотношений благ при потреблении.

Слайд 11 Чаще всего применяются
- линейная,
-квадратичная
-логарифмическая функции вида

Слайд 12 В качестве примера приведем конкретную квадратичную функцию полезности

В качестве примера приведем конкретную квадратичную функцию полезности для трех агрегированных

для трех агрегированных групп товаров, построенную на основе обработки

данных бюджетной статистики

Слайд 13

Слайд 14 Свойства функции полезности
1. С ростом потребления любого блага

Свойства функции полезности1. С ростом потребления любого блага полезность растет. Частные

полезность растет. Частные производные функции полезности, определяющие предельную полезность

всегда положительны

Слайд 15 2. Небольшой прирост блага при его первоначальном отсутствии

резко увеличивает полезность

Слайд 16 3. Предельная полезность каждого блага уменьшается, если объем

3. Предельная полезность каждого блага уменьшается, если объем его потребления растет,

его потребления растет, то есть каждая дополнительная единица приобретенного

блага используется менее эффективно. Скорость роста полезности замедляется. В этом случае вторые производные функции полезности отрицательны

Слайд 17 4. При очень большом объеме блага его дальнейшее

увеличение не приводит к увеличению полезности

Слайд 18 5. Предельная полезность каждого блага увеличивается, если

растет количество другого блага. В этом случае смешанные производные

второго порядка положительны

Слайд 19 Здесь благо, количество которого фиксировано, оказывается относительно дефицитным,

Здесь благо, количество которого фиксировано, оказывается относительно дефицитным, поэтому дополнительная его

поэтому дополнительная его единица приобретает большую ценность и используется

более эффективно. Данное свойство справедливо не для всех благ. Если блага могут полностью замещать друг друга в потреблении, то это свойство не выполняется, но оно гарантирует выпуклость вниз кривых безразличия.

Слайд 20 Графический анализ функции полезности. Линии уровня.

Рассмотрим функцию

Графический анализ функции полезности. Линии уровня. Рассмотрим функцию полезности U=U(x1,x2). Линией

полезности U=U(x1,x2). Линией уровня функции U=U(x1,x2) называется геометрическое место

точек плоскости (x1,x2), в которых функция принимает одно и то же значение равное q, U(x1,x2)=q. Пусть функция U=U(x1,x2) является степенной, например,

Слайд 21 Кривые безразличия.

Для функции полезности линии уровня называют линиями

Кривые безразличия.Для функции полезности линии уровня называют линиями или кривыми безразличия.

или кривыми безразличия.
Линия безразличия представляет собой геометрическое место

точек плоскости, каждая из которых представляет собой такую комбинацию материальных благ, которая обеспечивает одну и ту же полезность, и потребителю безразлично какую из точек на данной кривой выбирать.

Слайд 22 Типы кривых безразличия.

Линейная. Функция полезности с полным взаимозамещением

Типы кривых безразличия.Линейная. Функция полезности с полным взаимозамещением благ имеет вид

благ имеет вид
U=ax1+bx2,
где a и b –

параметры . Из функции полезности можно найти
x2=(U-ax1)/b
и построить кривые безразличия линейного типа

Слайд 23 Неоклассическая (степенная)
функция полезности

, где α+β

построим кривые безразличия неоклассическоо типа

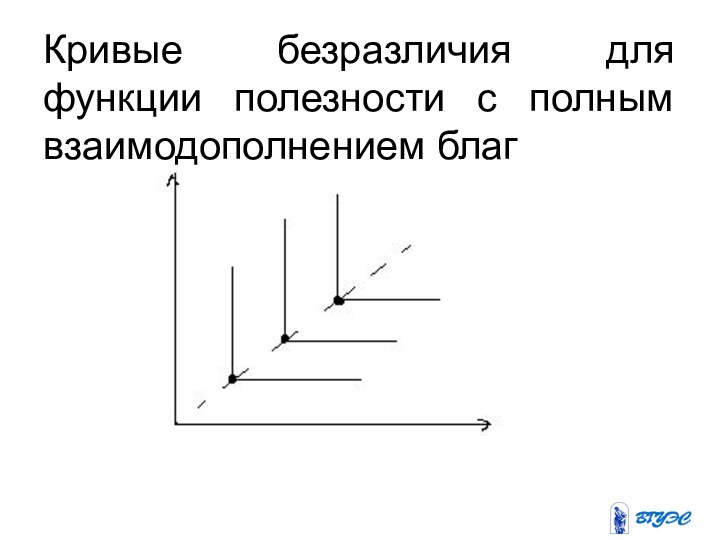
Слайд 24 С полным взаимодополнением благ

(например, при увеличении спроса

С полным взаимодополнением благ (например, при увеличении спроса на одно благо,

на одно благо, растёт спрос на другое благо) имеет

кривые безразличия в виде точки на пересечении двух прямых. Избыток одного блага не имеет значение.
Полезность достигается лишь приопределённой комбинации благ
U=min(x1/a;x2/b)

Слайд 25 Кривые безразличия для функции полезности с полным взаимодополнением

благ

Слайд 26 Свойства кривых безразличия

На основании аксиомы поведения потребителя кривая

Свойства кривых безразличияНа основании аксиомы поведения потребителя кривая безразличия, лежащая выше

безразличия, лежащая выше и правее другой кривой, представляет собой

более предпочтительные наборы благ.

Слайд 27 Кривые безразличия никогда не пересекаются, т.к. через любую

Кривые безразличия никогда не пересекаются, т.к. через любую точку на карте

точку на карте можно провести только одну кривую безразличия.

Слайд 28 Кривые безразличия имеют отрицательный наклон. Абсолютный наклон кривой

Кривые безразличия имеют отрицательный наклон. Абсолютный наклон кривой безразличия при движении

безразличия при движении вправо уменьшается, она становится более пологой.

Слайд 29 Предельная норма замещения благ.

Выражение

называют предельной нормой замещения

Предельная норма замещения благ.Выражение называют предельной нормой замещения первого блага вторым,

первого блага вторым, которая показывает, на сколько единиц увеличится

(уменьшится) потребление второго блага, при уменьшении (увеличении) потребления первого блага на единицу без изменения функции полезности.

Слайд 30
В общем виде формулу предельной нормы замещения благ

В общем виде формулу предельной нормы замещения благ записывают в виде

записывают в виде

которая показывает, на сколько увеличится (уменьшится)

потребление одного блага, при уменьшении (увеличении) потребления другого блага на единицу без изменения полезности.
Предельная норма замещения благ равна обратному соотношению предельных полезностей, взятому со знаком «-».